Probabilistic Robotics Course Presentation Outline 1 Introduction 2

Probabilistic Robotics Course Presentation Outline 1. Introduction 2. The Bayes Filter 3. Non Parametric Filters 4. Gausian Filters 5. EKF Map Based Localization 6. EKF Feature-based SLAM 7. EKF Pose-based SLAM 8. Advanced SLAM Concepts

Probabilistic Robotics 1 Introduction What is Probabilistic Robotics? ‘Robotics is the science of perceiving and manipulating the physical world through computer controlled mechanical devices. ’ ‘Probabilistic robotics is a relatively new approach to robotics that pays tribute to the uncertainty in robot perception and action. ’ Sebastian Thrun

Robot Probabilistic Robotics Localization 1 Introduction Probabilistic Robotics course Where am I? Localization Where are the amphoras? Mapping

Probabilistic Robotics 1 Introduction • Localization: Estimate the position, orientation and velocity of a vehicle • Localization through Dead Reckoning: Step : k+2 Step : k+1 Step: k The Uncertainty grows without bound. The vehicle gets lost Y {B} X

Probabilistic Robotics 1 Introduction • Localization through Dead-Reckoning: The robot position drifts
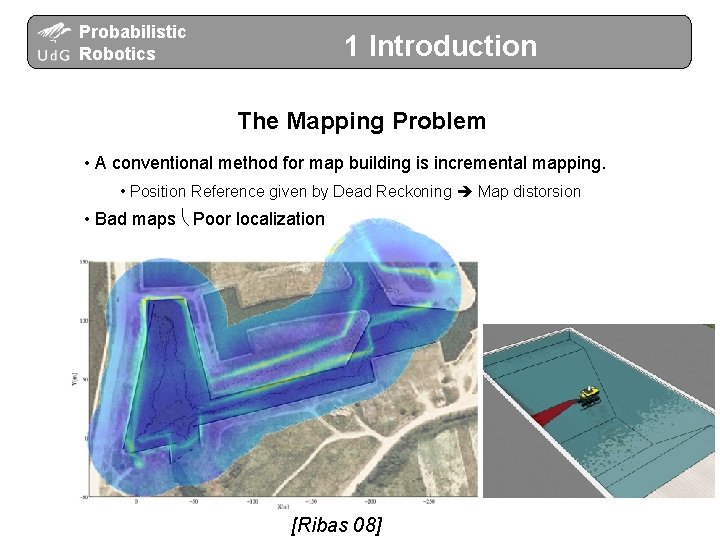
Probabilistic Robotics 1 Introduction The Mapping Problem • A conventional method for map building is incremental mapping. • Position Reference given by Dead Reckoning Map distorsion • Bad maps Poor localization [Ribas 08]
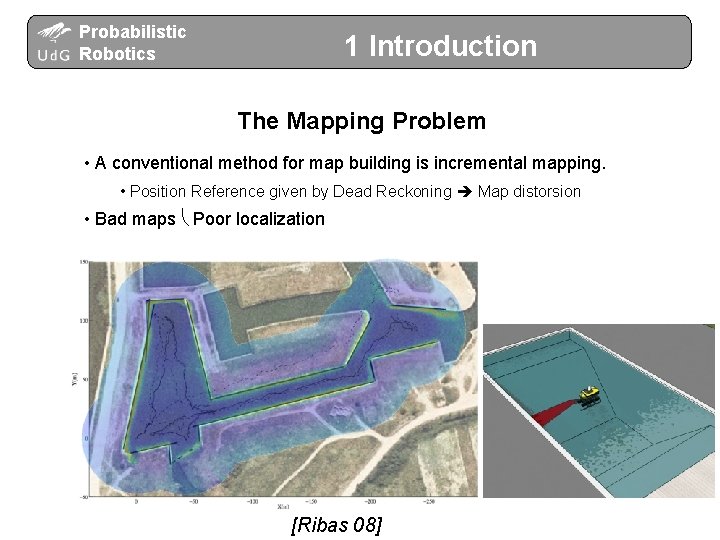
Probabilistic Robotics 1 Introduction The Mapping Problem • A conventional method for map building is incremental mapping. • Position Reference given by Dead Reckoning Map distorsion • Bad maps Poor localization [Ribas 08]

Probabilistic Robotics 1 Introduction This is an old problem… Ancient Europe. The Catalan Atlas of 1376.
Probabilistic Robotics 1 Introduction This is an old problem…
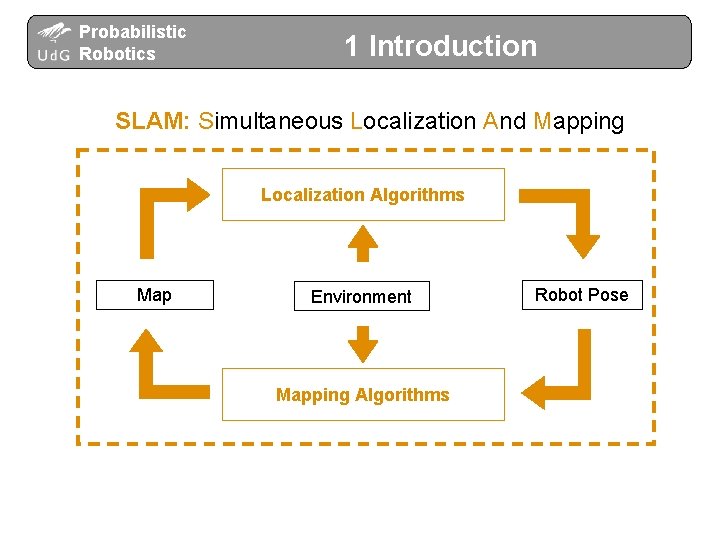
Probabilistic Robotics 1 Introduction SLAM: Simultaneous Localization And Mapping Localization Algorithms Map Environment Mapping Algorithms Robot Pose
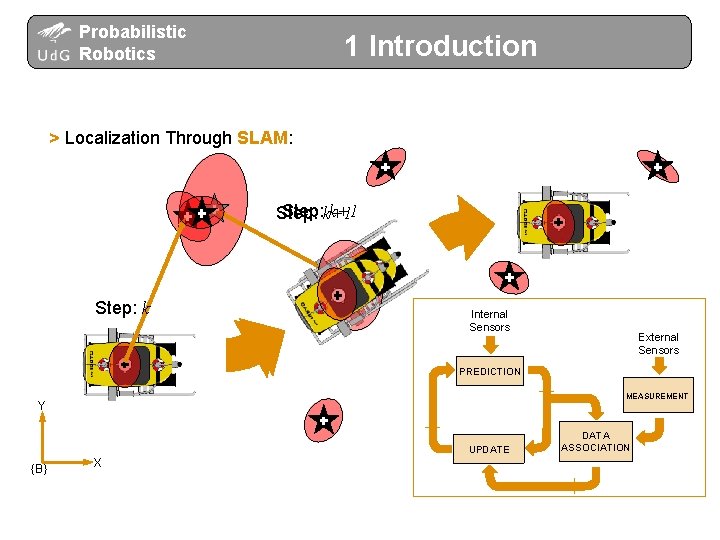
Probabilistic Robotics 1 Introduction > Localization Through SLAM: Step: k+1 Step: k Internal Sensors External Sensors PREDICTION MEASUREMENT Y UPDATE {B} X DATA ASSOCIATION
![Probabilistic Robotics 1 Introduction > Localization Through SLAM: [Ribas 08] Probabilistic Robotics 1 Introduction > Localization Through SLAM: [Ribas 08]](http://slidetodoc.com/presentation_image_h/113b047c98b65799a5beda49e6814e80/image-12.jpg)
Probabilistic Robotics 1 Introduction > Localization Through SLAM: [Ribas 08]

Probabilistic Robotics 1. 1 Problem Statement “Using sensory information to locate the robot in its environment is the most fundamental problem to providing a mobile robot with autonomous capabilities. ” [Cox ’ 91] • Given – Map of the environment. – Sequence of sensor measurements. • Wanted – Estimate of the robot’s position. • Problem classes – Position tracking (initial pose known) – Global localization (initial pose unknown) – Kidnapped robot problem (recovery)
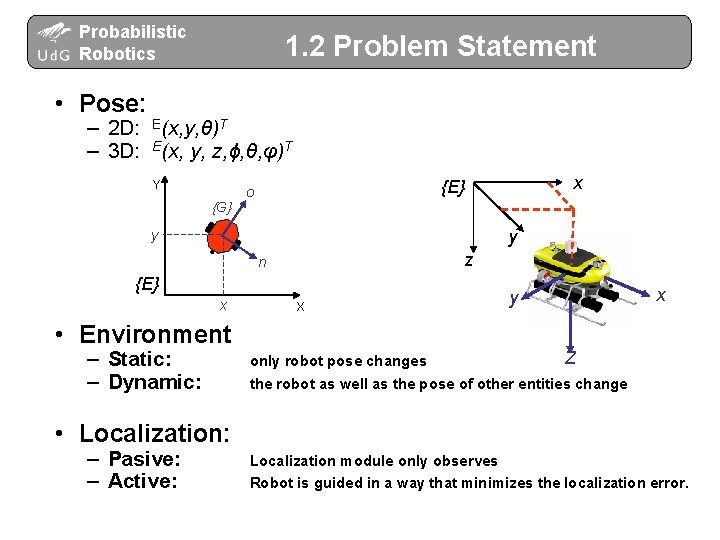
Probabilistic Robotics 1. 2 Problem Statement • Pose: – 2 D: E(x, y, θ)T – 3 D: E(x, y, z, ϕ, θ, φ)T Y {G} x {E} o y y z n {E} x X • Environment – Static: – Dynamic: only robot pose changes x y Z the robot as well as the pose of other entities change • Localization: – Pasive: – Active: Localization module only observes Robot is guided in a way that minimizes the localization error.
![Probabilistic Robotics Dead Reckoning: x {E} y z [xk yk θk] function get. Odometry() Probabilistic Robotics Dead Reckoning: x {E} y z [xk yk θk] function get. Odometry()](http://slidetodoc.com/presentation_image_h/113b047c98b65799a5beda49e6814e80/image-15.jpg)
Probabilistic Robotics Dead Reckoning: x {E} y z [xk yk θk] function get. Odometry() ΔNL=Read. Encoder(LEFT); ΔNR=Read. Encoder(RIGH T); dl = 2 * π * R * ((ΔNL)/ζ) ; dr = 2 * π * R * ((ΔNR)/ζ) ; d =(dr+dl)/2; Δθk=(dr-dl)/w; θk= θk-1+ Δθk; xk= xk-1 + (d * cos(θk)); y = y + (d * sin(θ )); y {B} z x
![Probabilistic Robotics Odometry of the differential drive [xk yk θk] function get. Odometry() ΔNL=Read. Probabilistic Robotics Odometry of the differential drive [xk yk θk] function get. Odometry() ΔNL=Read.](http://slidetodoc.com/presentation_image_h/113b047c98b65799a5beda49e6814e80/image-16.jpg)
Probabilistic Robotics Odometry of the differential drive [xk yk θk] function get. Odometry() ΔNL=Read. Encoder(LEFT); ΔNR=Read. Encoder(RIGH T); dl = 2 * π * R * ((ΔNL)/ζ) ; dr = 2 * π * R * ((ΔNR)/ζ) ; d =(dr+dl)/2; Δθk=(dr-dl)/w; θk= θk-1+ Δθk; xk= xk-1 + (d * cos(θk)); yk= yk-1 + (d * sin(θk)); Return [xkeach yk θk]Wheel turn ζ: pulses R: Wheel radious
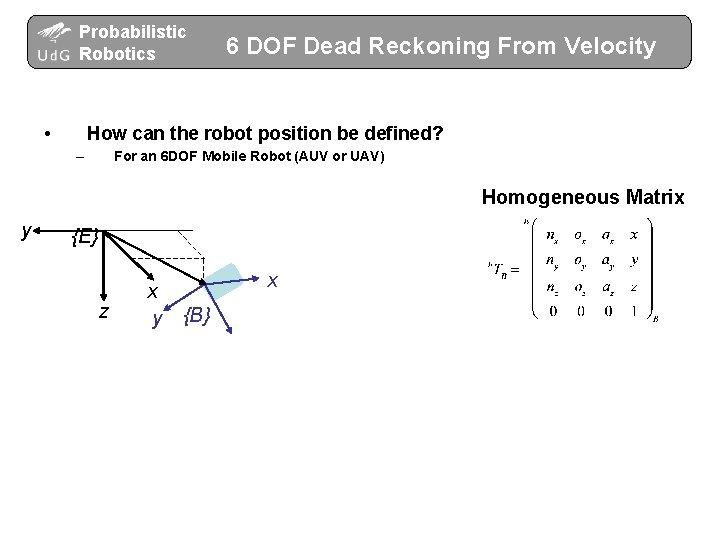
Probabilistic Robotics • 6 DOF Dead Reckoning From Velocity How can the robot position be defined? – For an 6 DOF Mobile Robot (AUV or UAV) Homogeneous Matrix y {E} z x y x {B}
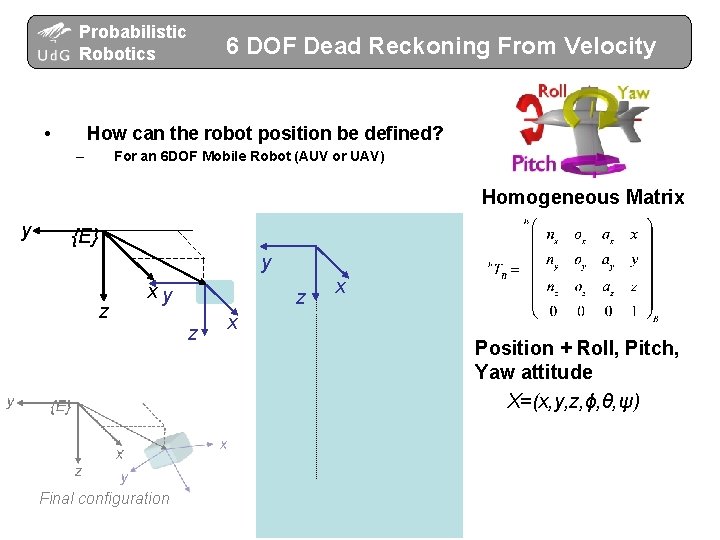
Probabilistic Robotics • 6 DOF Dead Reckoning From Velocity How can the robot position be defined? – For an 6 DOF Mobile Robot (AUV or UAV) Homogeneous Matrix y {E} y z xy Final configuration z z x x Position + Roll, Pitch, Yaw attitude X=(x, y, z, ϕ, θ, ψ)
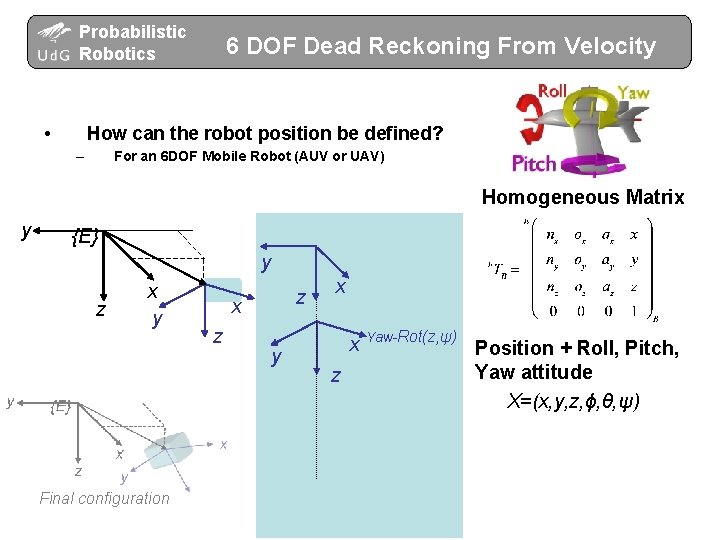
Probabilistic Robotics • 6 DOF Dead Reckoning From Velocity How can the robot position be defined? – For an 6 DOF Mobile Robot (AUV or UAV) Homogeneous Matrix y {E} y z x y Final configuration z x z y x x z Yaw-Rot(z, ψ) Position + Roll, Pitch, Yaw attitude X=(x, y, z, ϕ, θ, ψ)
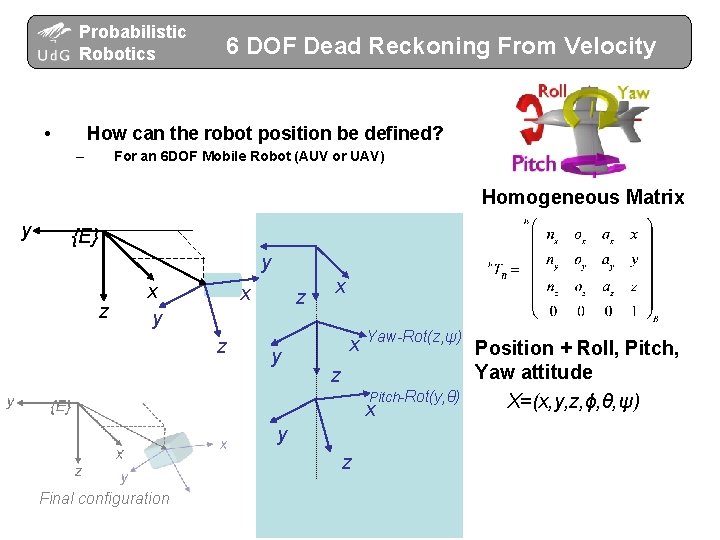
Probabilistic Robotics • 6 DOF Dead Reckoning From Velocity How can the robot position be defined? – For an 6 DOF Mobile Robot (AUV or UAV) Homogeneous Matrix y {E} y z x y x z z y x x Yaw-Rot(z, ψ) z Pitch-Rot(y, θ) x y z Final configuration Position + Roll, Pitch, Yaw attitude X=(x, y, z, ϕ, θ, ψ)
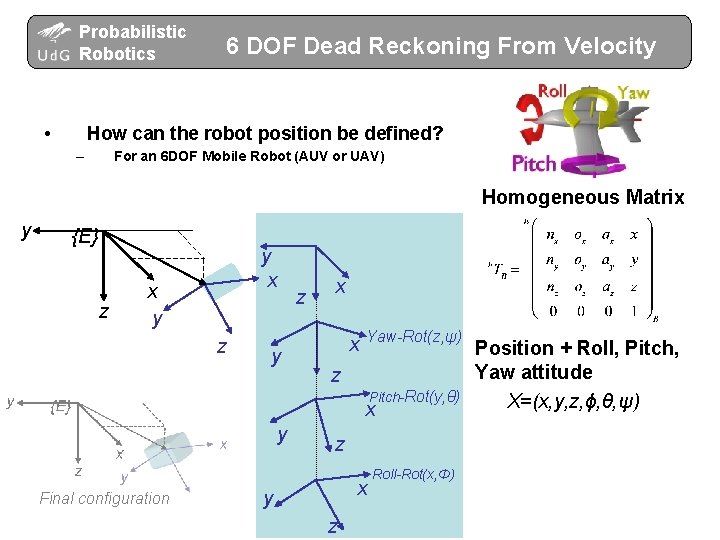
Probabilistic Robotics • 6 DOF Dead Reckoning From Velocity How can the robot position be defined? – For an 6 DOF Mobile Robot (AUV or UAV) Homogeneous Matrix y {E} z y x x y z x x Yaw-Rot(z, ψ) z Pitch-Rot(y, θ) x y Final configuration z x y z Roll-Rot(x, Φ) Position + Roll, Pitch, Yaw attitude X=(x, y, z, ϕ, θ, ψ)

Probabilistic Robotics • 6 DOF Dead Reckoning From Velocity How can the robot position be defined? – UUV Position & attitude Er=(x, – Homogeneous Matrix y, z, ϕ, θ, ψ)T
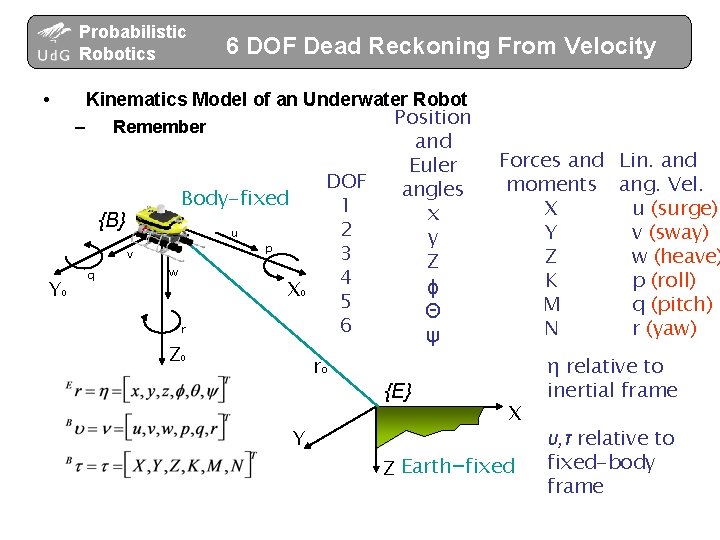
Probabilistic Robotics • Kinematics Model of an Underwater Robot – Remember Body-fixed {B} u v Y 6 DOF Dead Reckoning From Velocity q w p X 0 0 r Z DOF 1 2 3 4 5 6 ro 0 Y Position and Euler angles x y Z ϕ Θ ψ {E} Forces and Lin. and moments ang. Vel. X u (surge) Y v (sway) Z w (heave) K p (roll) M q (pitch) N r (yaw) X Z Earth-fixed η relative to inertial frame υ, τ relative to fixed-body frame
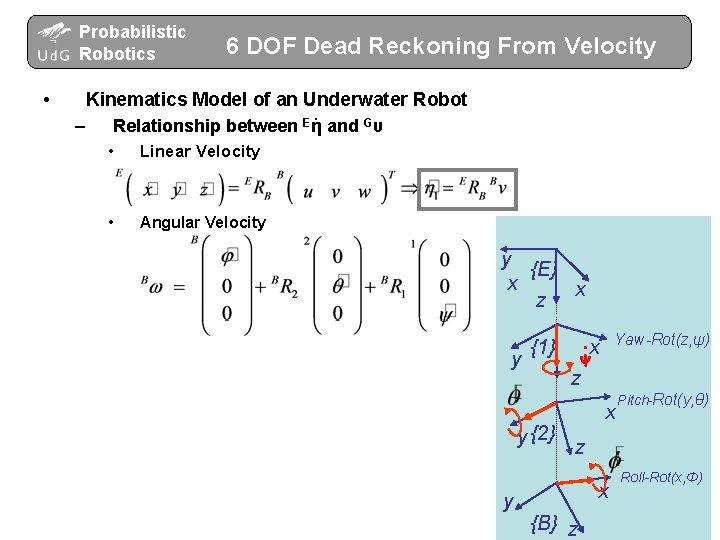
Probabilistic Robotics • 6 DOF Dead Reckoning From Velocity Kinematics Model of an Underwater Robot – . Relationship between Eη and Gυ • Linear Velocity • Angular Velocity y {E} x x z y {1} Yaw-Rot(z, ψ) x z y {2} x Pitch-Rot(y, θ) z x y {B} z Roll-Rot(x, Φ)
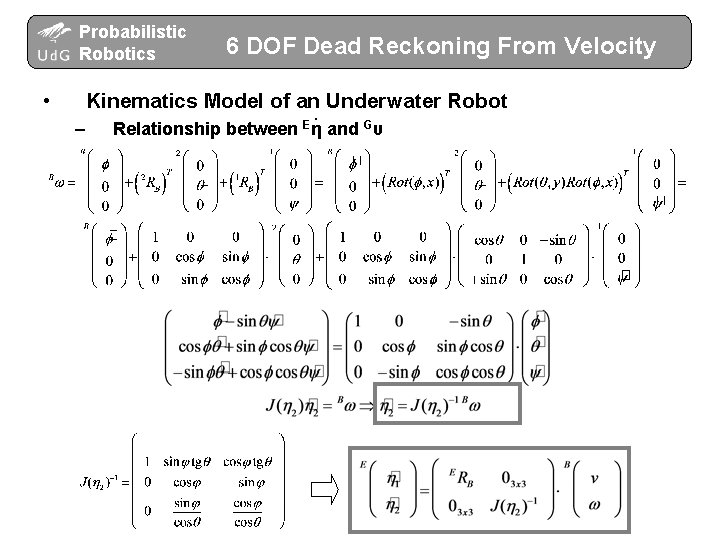
Probabilistic Robotics • – 6 DOF Dead Reckoning From Velocity Kinematics Model of an Underwater Robot. E G Relationship between η and υ
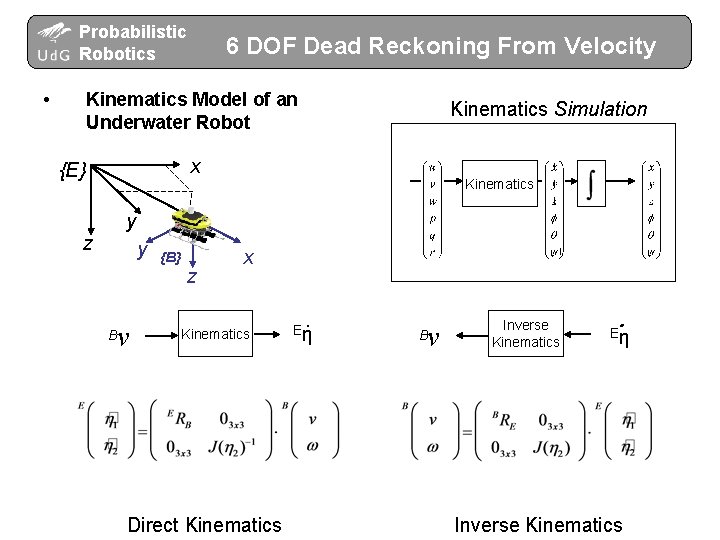
Probabilistic Robotics • 6 DOF Dead Reckoning From Velocity Kinematics Model of an Underwater Robot Kinematics Simulation x {E} Kinematics y z y v B {B} z x Kinematics Direct Kinematics . Eη v B Inverse Kinematics . Eη Inverse Kinematics
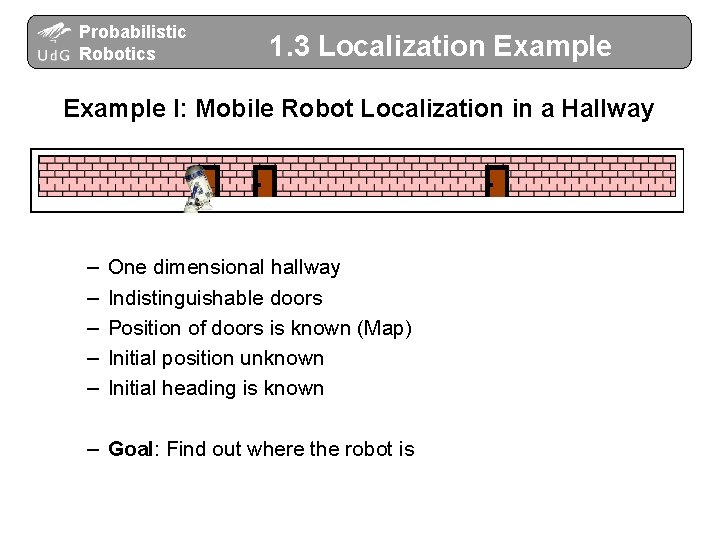
Probabilistic Robotics 1. 3 Localization Example I: Mobile Robot Localization in a Hallway – – – One dimensional hallway Indistinguishable doors Position of doors is known (Map) Initial position unknown Initial heading is known – Goal: Find out where the robot is
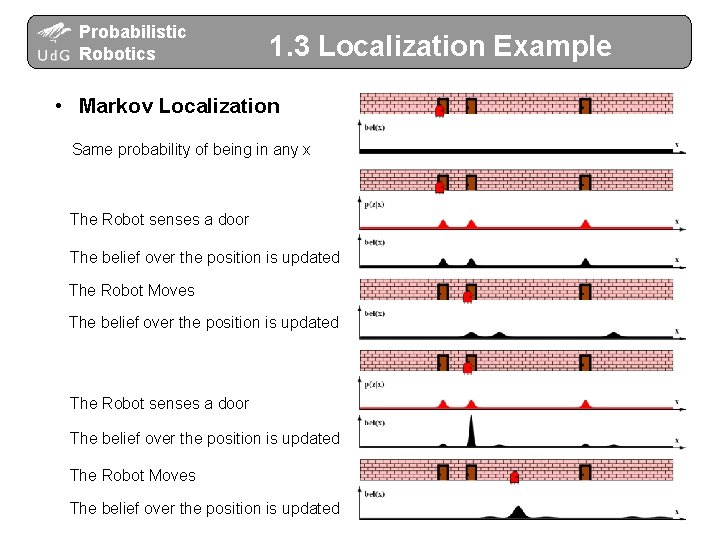
Probabilistic Robotics 1. 3 Localization Example • Markov Localization Same probability of being in any x The Robot senses a door The belief over the position is updated The Robot Moves The belief over the position is updated
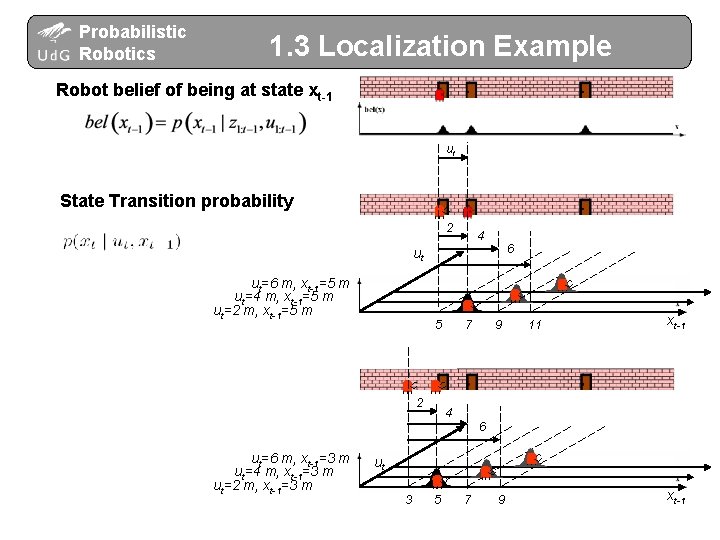
Probabilistic Robotics 1. 3 Localization Example Robot belief of being at state xt-1 ut State Transition probability 2 4 6 ut ut=6 m, xt-1=5 m ut=4 m, xt-1=5 m ut=2 m, xt-1=5 m 5 2 7 9 11 xt-1 4 6 ut=6 m, xt-1=3 m ut=4 m, xt-1=3 m ut=2 m, xt-1=3 m ut 3 5 7 9 xt-1
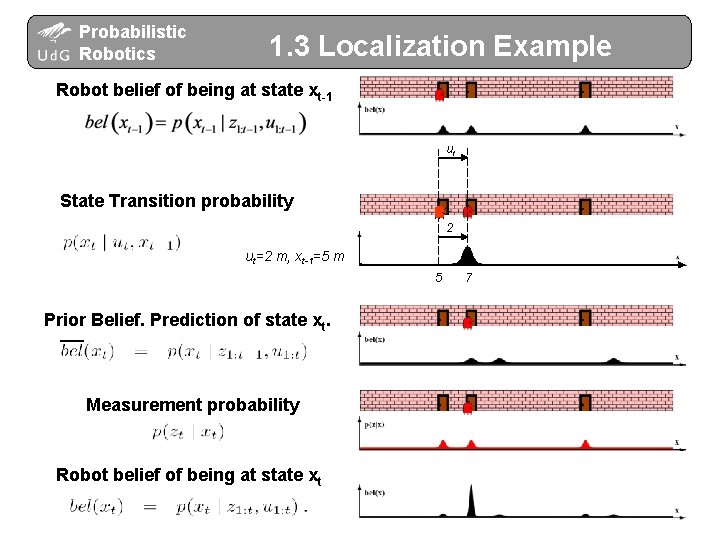
Probabilistic Robotics 1. 3 Localization Example Robot belief of being at state xt-1 ut State Transition probability 2 ut=2 m, xt-1=5 m 5 Prior Belief. Prediction of state xt. Measurement probability Robot belief of being at state xt 7
- Slides: 30