Probabilistic image processing and Bayesian network Kazuyuki Tanaka

Probabilistic image processing and Bayesian network Kazuyuki Tanaka Graduate School of Information Sciences, Tohoku University kazu@smapip. is. tohoku. ac. jp http: //www. smapip. is. tohoku. ac. jp/~kazu/ References K. Tanaka: Statistical-mechanical approach to image processing (Topical Review), J. Phys. A, vol. 35, pp. R 81 -R 150 (2002). K. Tanaka, H. Shouno, M. Okada and D. M. Titterington: Accuracy of the Bethe approximation for hyperparameter estimation in probabilistic image processing, J. Phys. A, vol. 37, pp. 8675 -8695 (2004). 8 November, 2005 CISJ 2005 1

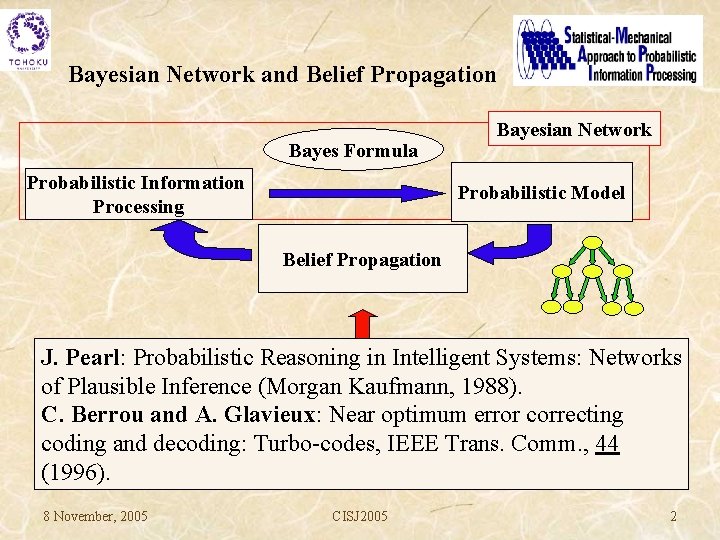
Bayesian Network and Belief Propagation Bayes Formula Probabilistic Information Processing Bayesian Network Probabilistic Model Belief Propagation J. Pearl: Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference (Morgan Kaufmann, 1988). C. Berrou and A. Glavieux: Near optimum error correcting coding and decoding: Turbo-codes, IEEE Trans. Comm. , 44 (1996). 8 November, 2005 CISJ 2005 2

Contents 1. Introduction 2. Belief Propagation 3. Bayesian Image Analysis and Gaussian Graphical Model 4. Concluding Remarks 8 November, 2005 CISJ 2005 3

Belief Propagation How should we treat the calculation of the summation over 2 N configuration? It is very hard to calculate exactly except some special cases. Formulation for approximate algorithm Accuracy of the approximate algorithm 8 November, 2005 CISJ 2005 4

Tractable Model Probabilistic models with no loop are tractable. Factorizable Probabilistic models with loop are not tractable. Not Factorizable 8 November, 2005 CISJ 2005 5

Probabilistic model on a graph with no loop Marginal probability of the node 2 3 2 6 8 November, 2005 CISJ 2005 4 1 5 6

Probabilistic model on a graph with no loop 3 2 6 8 November, 2005 4 1 5 Marginal probability can be expressed in terms of the product of messages from all the neighbouring nodes of node 2. Message from the node 1 to the node 2 can be expressed in terms of the product of message from all the neighbouring nodes of the node 1 except one from the node 2. CISJ 2005 7

Probabilistic Model on a Graph with Loops Marginal Probability 8 November, 2005 CISJ 2005 8

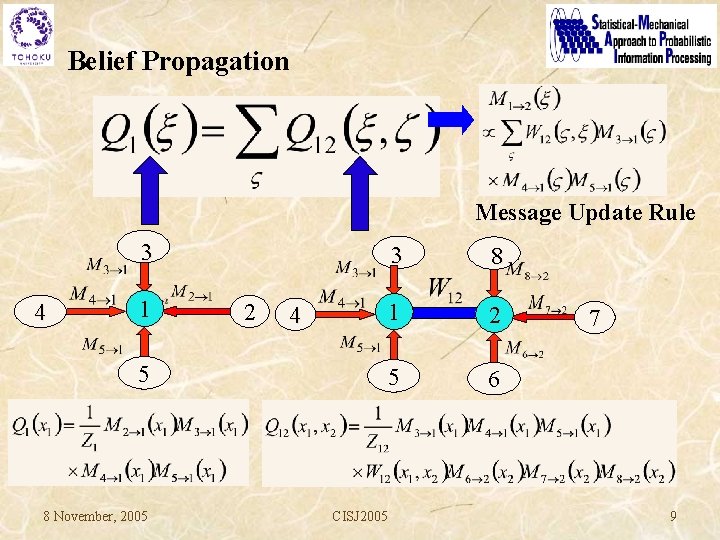
Belief Propagation Message Update Rule 3 4 1 2 4 5 8 November, 2005 CISJ 2005 3 8 1 2 5 6 7 9

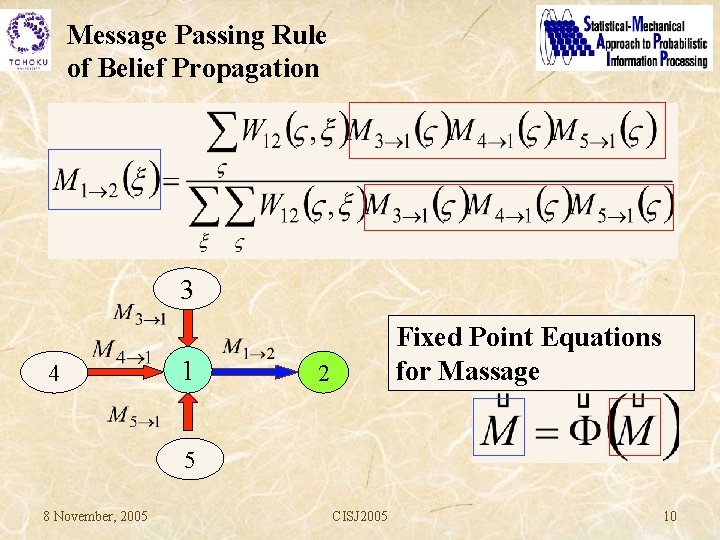
Message Passing Rule of Belief Propagation 3 4 1 Fixed Point Equations for Massage 2 5 8 November, 2005 CISJ 2005 10

Fixed Point Equation and Iterative Method Fixed Point Equation Iterative Method 8 November, 2005 CISJ 2005 11

Contents 1. Introduction 2. Belief Propagation 3. Bayesian Image Analysis and Gaussian Graphical Model 4. Concluding Remarks 8 November, 2005 CISJ 2005 12

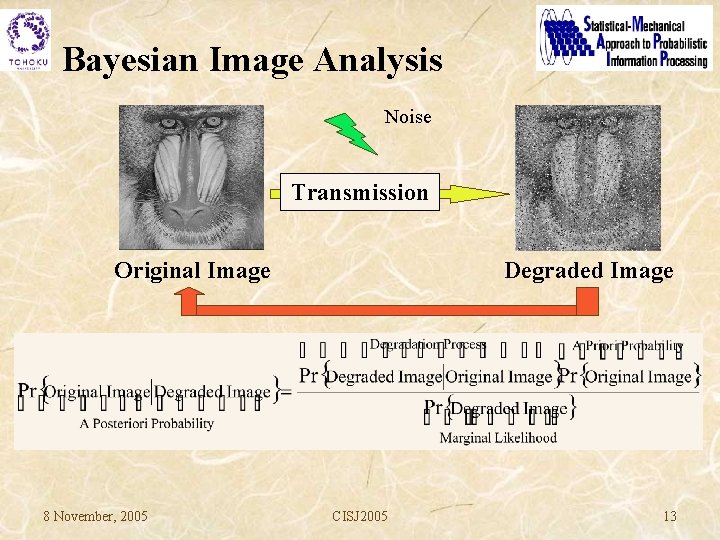
Bayesian Image Analysis Noise Transmission Original Image 8 November, 2005 Degraded Image CISJ 2005 13

Bayesian Image Analysis Degradation Process Additive White Gaussian Noise Transmission Original Image 8 November, 2005 Degraded Image CISJ 2005 14

Bayesian Image Analysis A Priori Probability Generate Similar? Standard Images 8 November, 2005 CISJ 2005 15

Bayesian Image Analysis A Posteriori Probability Gaussian Graphical Model 8 November, 2005 CISJ 2005 16

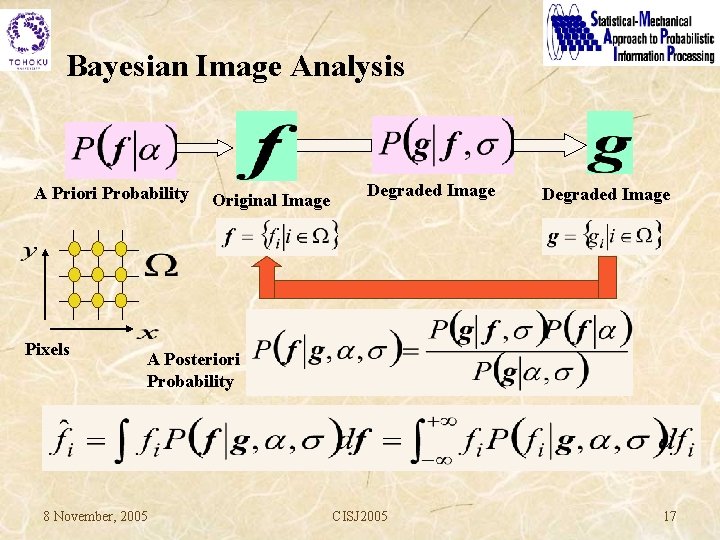
Bayesian Image Analysis A Priori Probability Pixels Original Image Degraded Image A Posteriori Probability 8 November, 2005 CISJ 2005 17

Hyperparameter Determination by Maximization of Marginal Likelihood Marginalization Degraded Image Original Image Marginal Likelihood 8 November, 2005 CISJ 2005 18

Maximization of Marginal Likelihood by EM (Expectation Maximization) Algorithm Marginal Likelihood Q-Function Incomplete Data Equivalent 8 November, 2005 CISJ 2005 19

Maximization of Marginal Likelihood by EM (Expectation Maximization) Algorithm Marginal Likelihood Q-Function EM Algorithm Iterate the following EM-steps until convergence: A. P. Dempster, N. M. Laird and D. B. Rubin, “Maximum likelihood from incomplete data via the EM algorithm, ” J. Roy. Stat. Soc. B, 39 (1977). 8 November, 2005 CISJ 2005 20

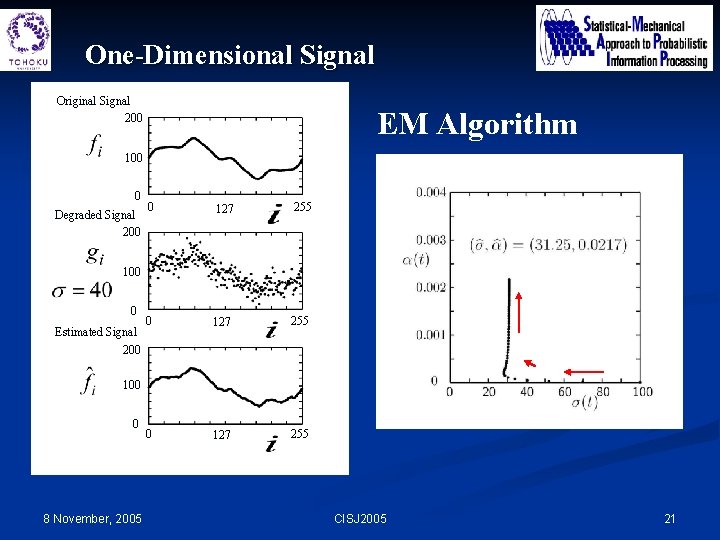
One-Dimensional Signal Original Signal 200 EM Algorithm 100 0 Degraded Signal 200 0 127 255 100 0 Estimated Signal 200 100 0 8 November, 2005 CISJ 2005 21

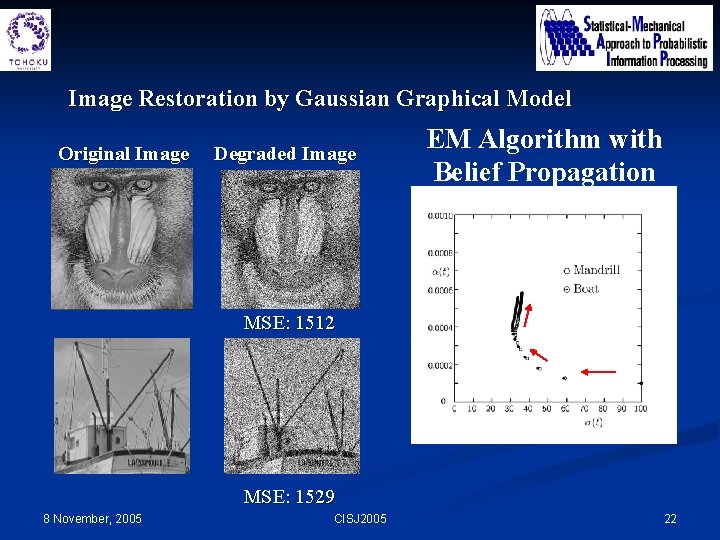
Image Restoration by Gaussian Graphical Model Original Image Degraded Image EM Algorithm with Belief Propagation MSE: 1512 MSE: 1529 8 November, 2005 CISJ 2005 22

Exact Results of Gaussian Graphical Model Multi-dimensional Gauss integral formula 8 November, 2005 CISJ 2005 23

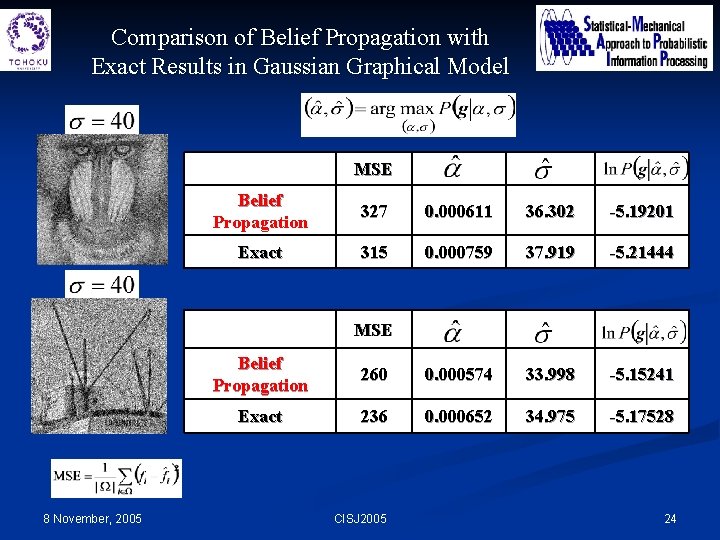
Comparison of Belief Propagation with Exact Results in Gaussian Graphical Model MSE Belief Propagation 327 0. 000611 36. 302 -5. 19201 Exact 315 0. 000759 37. 919 -5. 21444 MSE 8 November, 2005 Belief Propagation 260 0. 000574 33. 998 -5. 15241 Exact 236 0. 000652 34. 975 -5. 17528 CISJ 2005 24

Image Restoration by Gaussian Graphical Model Original Image Degraded Image Belief Propagation MSE: 1512 Lowpass Filter MSE: 411 8 November, 2005 MSE: 325 Wiener Filter Median Filter MSE: 545 MSE: 447 CISJ 2005 Exact MSE: 315 25

Image Restoration by Gaussian Graphical Model Original Image Degraded Image Belief Propagation MSE: 1529 Lowpass Filter MSE: 224 8 November, 2005 Wiener Filter MSE: 372 CISJ 2005 MSE: 260 Exact MSE 236 Median Filter MSE: 244 26

Extension of Belief Propagation Generalized Belief Propagation J. S. Yedidia, W. T. Freeman and Y. Weiss: Constructing free-energy approximations and generalized belief propagation algorithms, IEEE Transactions on Information Theory, 51 (2005). Generalized belief propagation is equivalent to the cluster variation method in statistical mechanics R. Kikuchi: A theory of cooperative phenomena, Phys. Rev. , 81 (1951). T. Morita: Cluster variation method of cooperative phenomena and its generalization I, J. Phys. Soc. Jpn, 12 (1957). 8 November, 2005 CISJ 2005 27

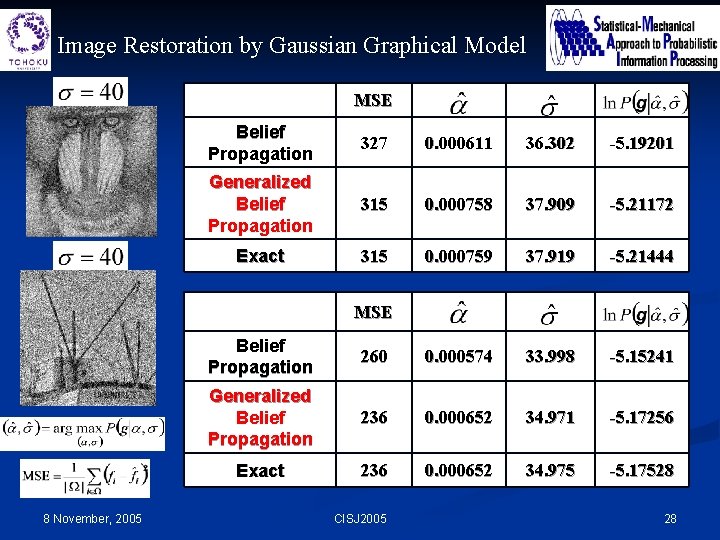
Image Restoration by Gaussian Graphical Model MSE Belief Propagation 327 0. 000611 36. 302 -5. 19201 Generalized Belief Propagation 315 0. 000758 37. 909 -5. 21172 Exact 315 0. 000759 37. 919 -5. 21444 MSE 8 November, 2005 Belief Propagation 260 0. 000574 33. 998 -5. 15241 Generalized Belief Propagation 236 0. 000652 34. 971 -5. 17256 Exact 236 0. 000652 34. 975 -5. 17528 CISJ 2005 28

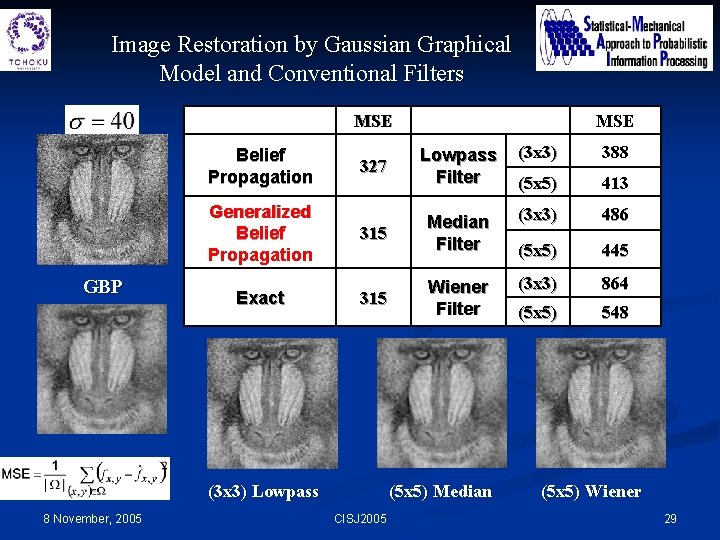
Image Restoration by Gaussian Graphical Model and Conventional Filters MSE 327 Lowpass Filter (3 x 3) 388 (5 x 5) 413 Generalized Belief Propagation 315 Median Filter (3 x 3) 486 (5 x 5) 445 Exact 315 Wiener Filter (3 x 3) 864 (5 x 5) 548 Belief Propagation GBP (3 x 3) Lowpass 8 November, 2005 MSE (5 x 5) Median CISJ 2005 (5 x 5) Wiener 29

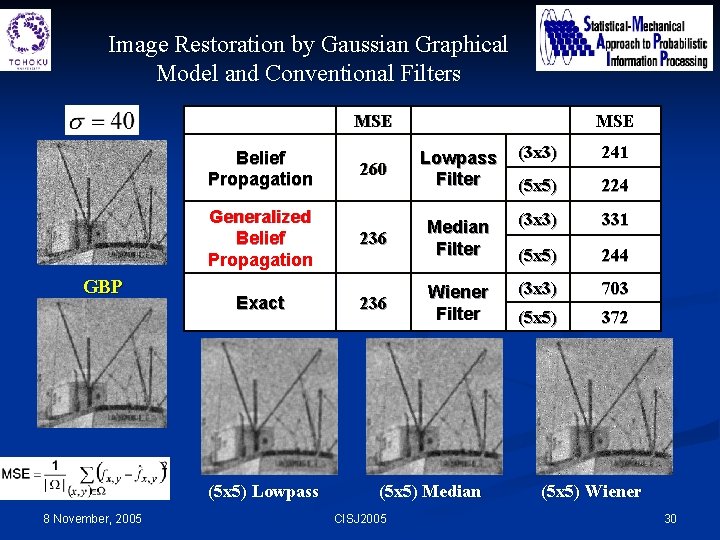
Image Restoration by Gaussian Graphical Model and Conventional Filters MSE Belief Propagation Generalized Belief Propagation GBP Exact (5 x 5) Lowpass 8 November, 2005 MSE 260 Lowpass Filter (3 x 3) 241 (5 x 5) 224 236 Median Filter (3 x 3) 331 (5 x 5) 244 236 Wiener Filter (3 x 3) 703 (5 x 5) 372 (5 x 5) Median CISJ 2005 (5 x 5) Wiener 30

Contents 1. Introduction 2. Belief Propagation 3. Bayesian Image Analysis and Gaussian Graphical Model 4. Concluding Remarks 8 November, 2005 CISJ 2005 31

Summary Formulation of belief propagation n Accuracy of belief propagation in Bayesian image analysis by means of Gaussian graphical model (Comparison between the belief propagation and exact calculation) n 8 November, 2005 CISJ 2005 32