Probabilistic Graphical Models Introduction Preliminaries Factors Daphne Koller

Probabilistic Graphical Models Introduction Preliminaries: Factors Daphne Koller

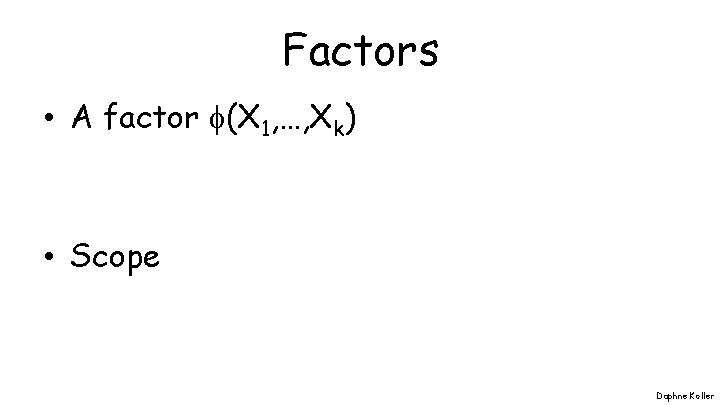
Factors • A factor (X 1, …, Xk) • Scope Daphne Koller

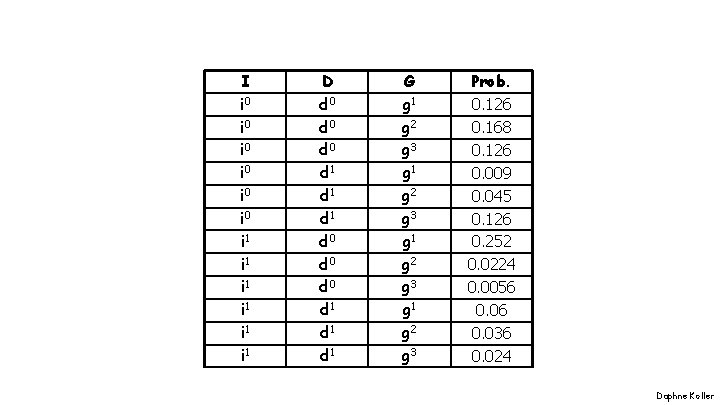
I i 0 i 0 i 0 i 1 i 1 i 1 D d 0 d 0 d 0 d 1 d 1 d 1 G g 1 g 2 g 3 Prob. 0. 126 0. 168 0. 126 0. 009 0. 045 0. 126 0. 252 0. 0224 0. 0056 0. 036 0. 024 Daphne Koller

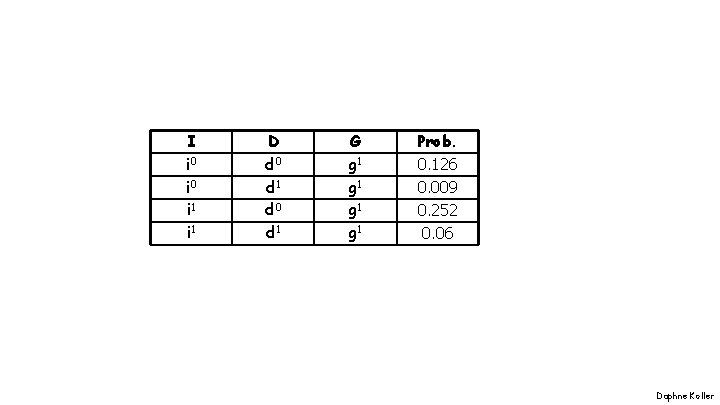
I i 0 i 1 D d 0 d 1 G g 1 g 1 Prob. 0. 126 0. 009 0. 252 0. 06 Daphne Koller

i 0, d 0 i 0, d 1 i 1, d 0 i 1, d 1 g 1 0. 3 0. 05 0. 9 0. 5 g 2 0. 4 0. 25 0. 08 0. 3 g 3 0. 7 0. 02 0. 2 P(G | I, D) Daphne Koller

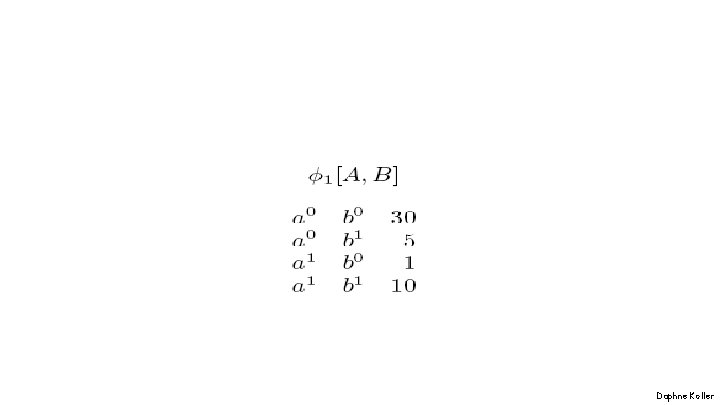
Daphne Koller

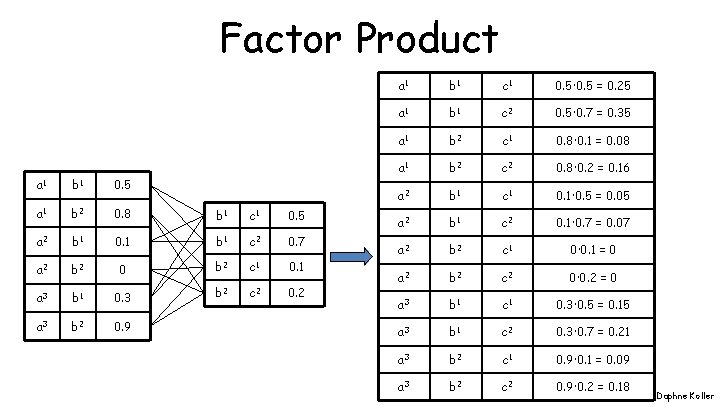
Factor Product a 1 b 1 0. 5 a 1 b 2 0. 8 b 1 c 1 0. 5 a 2 b 1 0. 1 b 1 c 2 0. 7 0 b 2 c 1 0. 1 b 2 c 2 0. 2 a 2 b 2 a 3 b 1 0. 3 a 3 b 2 0. 9 a 1 b 1 c 1 0. 5· 0. 5 = 0. 25 a 1 b 1 c 2 0. 5· 0. 7 = 0. 35 a 1 b 2 c 1 0. 8· 0. 1 = 0. 08 a 1 b 2 c 2 0. 8· 0. 2 = 0. 16 a 2 b 1 c 1 0. 1· 0. 5 = 0. 05 a 2 b 1 c 2 0. 1· 0. 7 = 0. 07 a 2 b 2 c 1 0· 0. 1 = 0 a 2 b 2 c 2 0· 0. 2 = 0 a 3 b 1 c 1 0. 3· 0. 5 = 0. 15 a 3 b 1 c 2 0. 3· 0. 7 = 0. 21 a 3 b 2 c 1 0. 9· 0. 1 = 0. 09 a 3 b 2 c 2 0. 9· 0. 2 = 0. 18 Daphne Koller

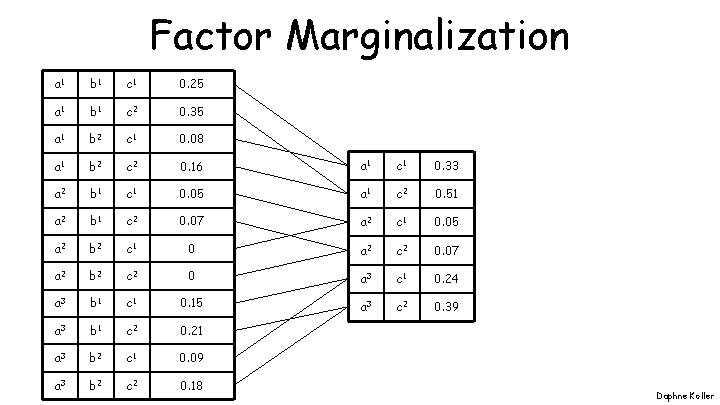
Factor Marginalization a 1 b 1 c 1 0. 25 a 1 b 1 c 2 0. 35 a 1 b 2 c 1 0. 08 a 1 b 2 c 2 0. 16 a 1 c 1 0. 33 a 2 b 1 c 1 0. 05 a 1 c 2 0. 51 a 2 b 1 c 2 0. 07 a 2 c 1 0. 05 a 2 b 2 c 1 0 a 2 c 2 0. 07 a 2 b 2 c 2 0 a 3 c 1 0. 24 a 3 b 1 c 1 0. 15 a 3 c 2 0. 39 a 3 b 1 c 2 0. 21 a 3 b 2 c 1 0. 09 a 3 b 2 c 2 0. 18 Daphne Koller

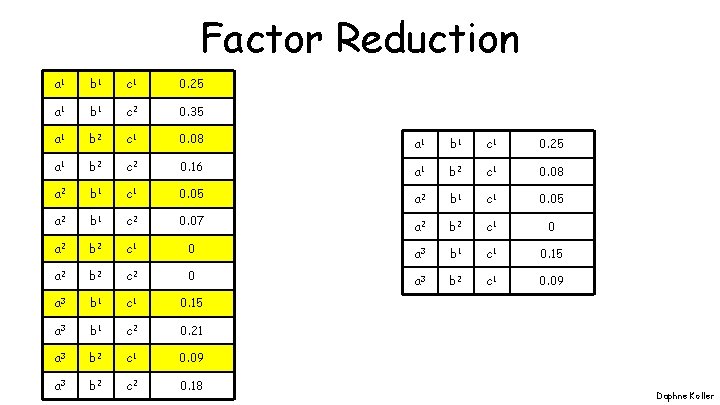
Factor Reduction a 1 b 1 c 1 0. 25 a 1 b 1 c 2 0. 35 a 1 b 2 c 1 0. 08 a 1 b 1 c 1 0. 25 a 1 b 2 c 2 0. 16 a 1 b 2 c 1 0. 08 a 2 b 1 c 1 0. 05 a 2 b 1 c 2 0. 07 a 2 b 2 c 1 0 a 3 b 1 c 1 0. 15 a 2 b 2 c 2 0 a 3 b 2 c 1 0. 09 a 3 b 1 c 1 0. 15 a 3 b 1 c 2 0. 21 a 3 b 2 c 1 0. 09 a 3 b 2 c 2 0. 18 Daphne Koller

END END Daphne Koller

Suppose q is at a local minimum of a function. What will one iteration of gradient descent do? Leave q unchanged. Change q in a random direction. Move q towards the global minimum of J(q). Decrease q.

Consider the weight update: Which of these is a correct vectorized implementation?

Fig. A corresponds to a=0. 01, Fig. B to a=0. 1, Fig. C to a=1. Fig. A corresponds to a=0. 1, Fig. B to a=0. 01, Fig. C to a=1. Fig. A corresponds to a=1, Fig. B to a=0. 01, Fig. C to a=0. 1. Fig. A corresponds to a=1, Fig. B to a=0. 1, Fig. C to a=0. 01.

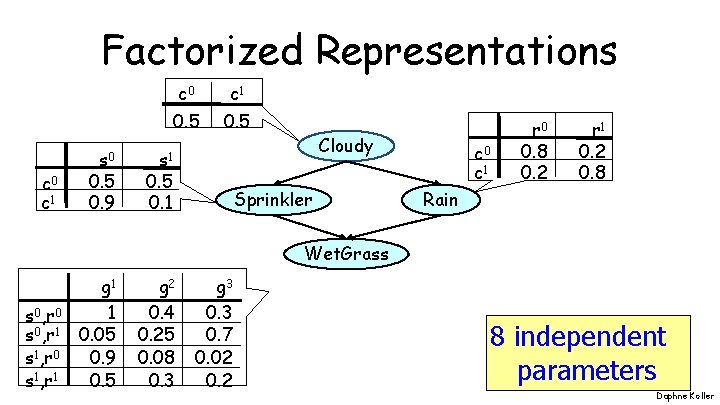
Factorized Representations c 0 c 1 s 0 0. 5 0. 9 c 0 c 1 0. 5 s 1 0. 5 0. 1 Cloudy Sprinkler c 0 c 1 r 0 0. 8 0. 2 r 1 0. 2 0. 8 Rain Wet. Grass s 0, r 0 s 0, r 1 s 1, r 0 s 1, r 1 g 1 1 0. 05 0. 9 0. 5 g 2 0. 4 0. 25 0. 08 0. 3 g 3 0. 7 0. 02 0. 2 8 independent parameters Daphne Koller