Probabilistic Graphical Models Inference Variable Elimination Algorithm Daphne

Probabilistic Graphical Models Inference Variable Elimination Algorithm Daphne Koller

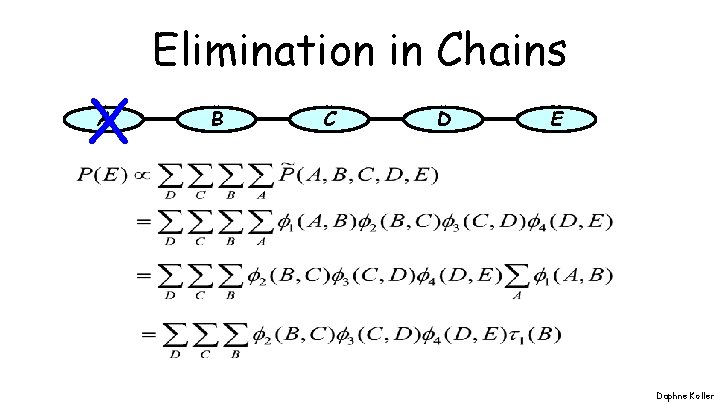
X A Elimination in Chains B C D E Daphne Koller

X A Elimination in Chains X B C D E Daphne Koller

Variable Elimination • Goal: P(J) • Eliminate: C, D, I, H, G, S, L C Compute I D G S L H J Daphne Koller

Variable Elimination • Goal: P(J) • Eliminate: D, I, H, G, S, L C Compute I D G S L H J Daphne Koller

Variable Elimination • Goal: P(J) • Eliminate: I, H, G, S, L C Compute I D G S L H J Daphne Koller

Variable Elimination • Goal: P(J) • Eliminate: H, G, S, L C Compute I D G S L H J Daphne Koller

Variable Elimination • Goal: P(J) • Eliminate: G, S, L C Compute I D G S L H J Daphne Koller

Variable Elimination • Goal: P(J) • Eliminate: S, L C I D G S L H J Daphne Koller

Variable Elimination with evidence • Goal: P(J, I=i, H=h) • Eliminate: C, D, G, S, L C I D G How do we get P(J | I=i, H=h)? S L H J Daphne Koller

Variable Elimination in MNs • Goal: P(D) • Eliminate: A, B, C A D At the end of elimination get 3(D) B C Daphne Koller

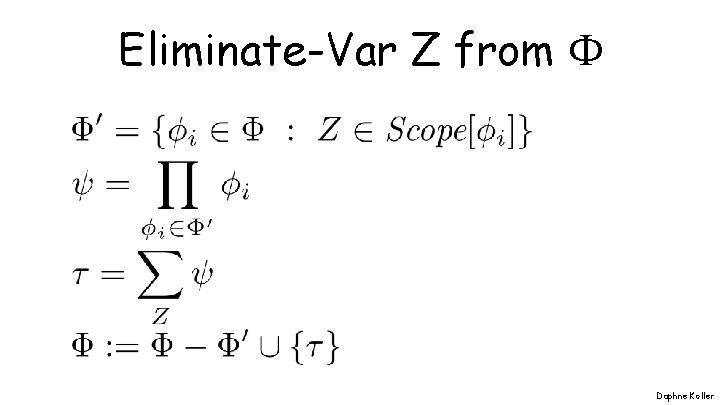
Eliminate-Var Z from Daphne Koller

VE Algorithm Summary • Reduce all factors by evidence – Get a set of factors • For each non-query variable Z – Eliminate-Var Z from • Multiply all remaining factors • Renormalize to get distribution Daphne Koller

Summary • Simple algorithm • Works for both BNs and MNs • Factor product and summation steps can be done in any order, subject to: – when Z is eliminated, all factors involving Z have been multiplied in Daphne Koller