Probabilistic Graphical Models Inference Message Passing Cluster Graph

Probabilistic Graphical Models Inference Message Passing Cluster Graph Properties Daphne Koller

Cluster Graphs • Undirected graph such that: – nodes are clusters Ci {X 1, …, Xn} – edge between Ci and Cj associated with sepset Si, j Ci Cj Daphne Koller

Family Preservation • Given set of factors , we assign each k to a cluster C (k) s. t. Scope[ k] C (k) • For each factor k , there exists a cluster Ci s. t. Scope[ k] Ci Daphne Koller

Running Intersection Property • For each pair of clusters Ci, Cj and variable X Ci Cj there exists a unique path between Ci and Cj for which all clusters and sepsets contain X C 1 C 4 C 7 C 3 C 6 C 5 C 2 Daphne Koller

Running Intersection Property • Equivalently: For any X, the set of clusters and sepsets containing X forms a tree C 1 C 4 C 7 C 3 C 6 C 5 C 2 Daphne Koller

Example Cluster Graph 1: A, B, C B 4: B, E C B E 2: B, C, D D 5: D, E B D 3: B, D, F Daphne Koller

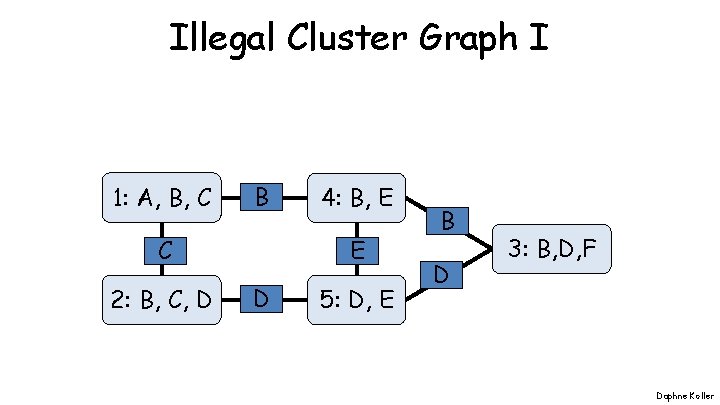
Illegal Cluster Graph I 1: A, B, C B C 2: B, C, D 4: B, E E D 5: D, E B D 3: B, D, F Daphne Koller

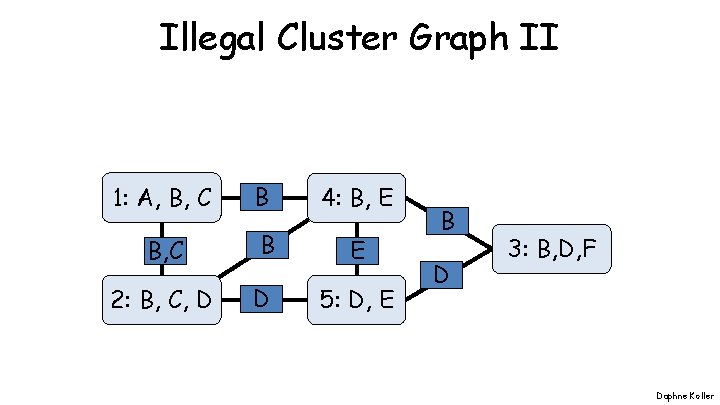
Illegal Cluster Graph II 1: A, B, C B 4: B, E B, C B E 2: B, C, D D 5: D, E B D 3: B, D, F Daphne Koller

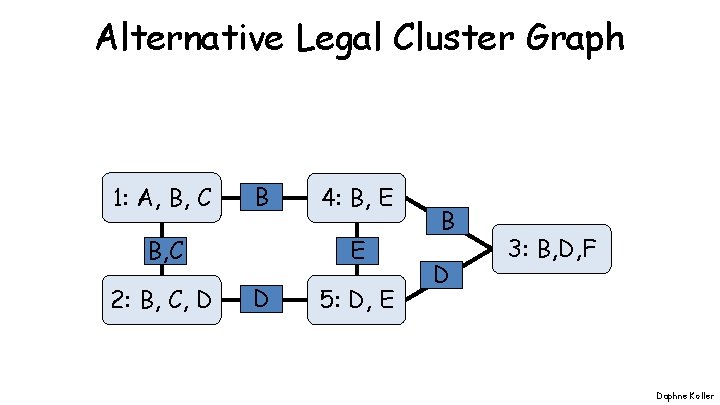
Alternative Legal Cluster Graph 1: A, B, C B B, C 2: B, C, D 4: B, E E D 5: D, E B D 3: B, D, F Daphne Koller

Bethe Cluster Graph • For each k , a factor cluster Ck =Scope[ k] • For each Xi a singleton cluster {Xi} • Edge Ck Xi if Xi Ck 1: A, B, C 6: A 2: B, C, D 7: B 8: C 3: B, D, F 9: D 4: B, E 10: E 5: D, E 11: F Daphne Koller

Summary • Cluster graph must satisfy two properties – family preservation: allows to be encoded – running intersection: connects all information about any variable, but without feedback loops • Bethe cluster graph is often first default • Richer cluster graph structures can offer different tradeoffs wrt computational cost and preservation of dependencies Daphne Koller

END END Daphne Koller