Probabilistic Graphical Models Acting Decision Making Utility Functions

Probabilistic Graphical Models Acting Decision Making Utility Functions Daphne Koller

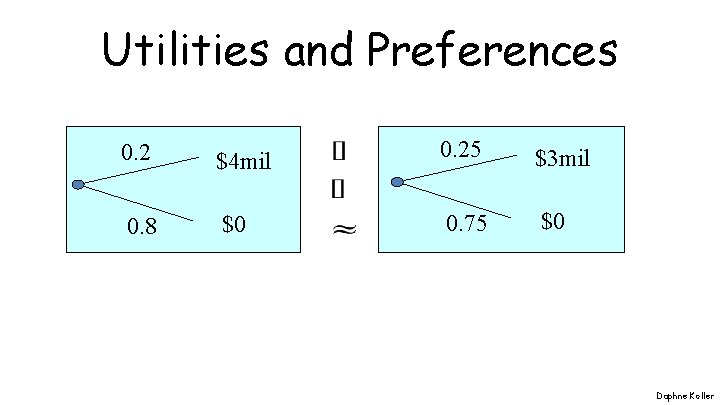
Utilities and Preferences 0. 2 $4 mil 0. 25 $3 mil 0. 8 $0 0. 75 $0 Daphne Koller

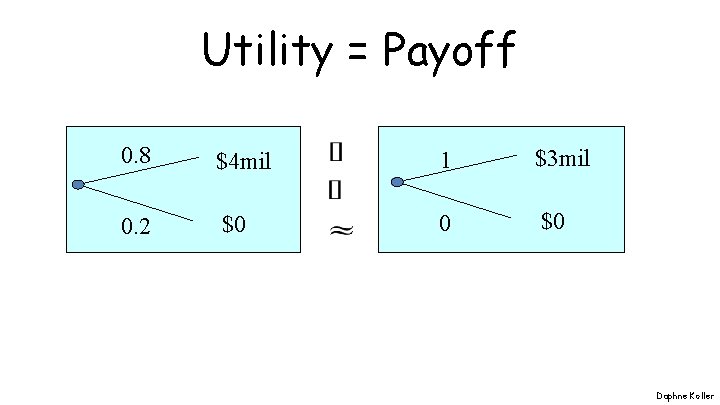
Utility = Payoff 0. 8 $4 mil 1 $3 mil 0. 2 $0 0 $0 Daphne Koller

St. Petersburg Paradox • Fair coin is tossed repeatedly until it comes up heads, say on the nth toss • Payoff = $2 n Daphne Koller

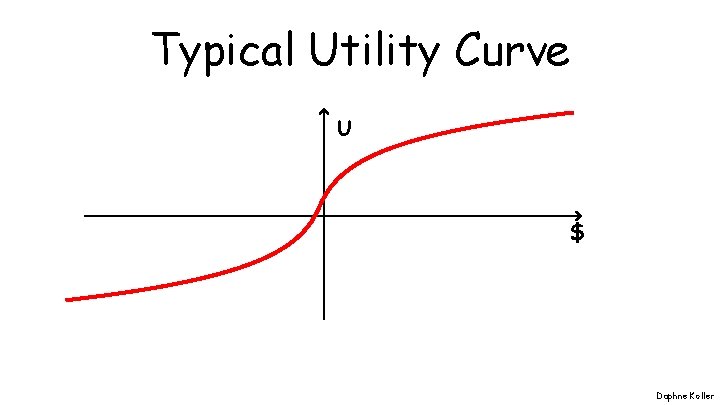
Typical Utility Curve U $ Daphne Koller

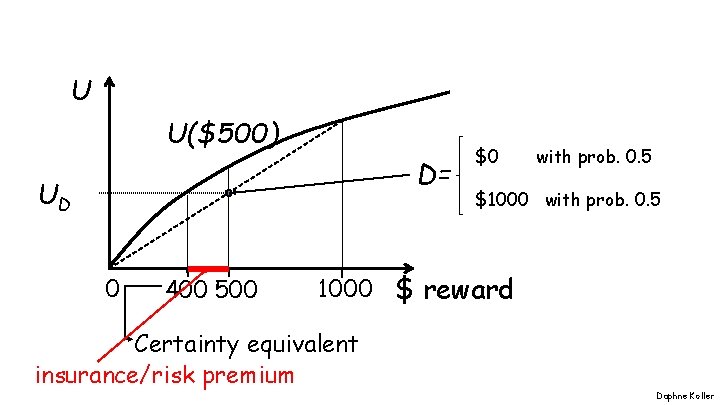
U U($500) D= UD 0 400 500 $0 with prob. 0. 5 $1000 with prob. 0. 5 1000 $ reward Certainty equivalent insurance/risk premium Daphne Koller

Multi-Attribute Utilities • All attributes affecting preferences must be integrated into one utility function • Human life – Micromorts – QALY (quality-adjusted life year) Daphne Koller

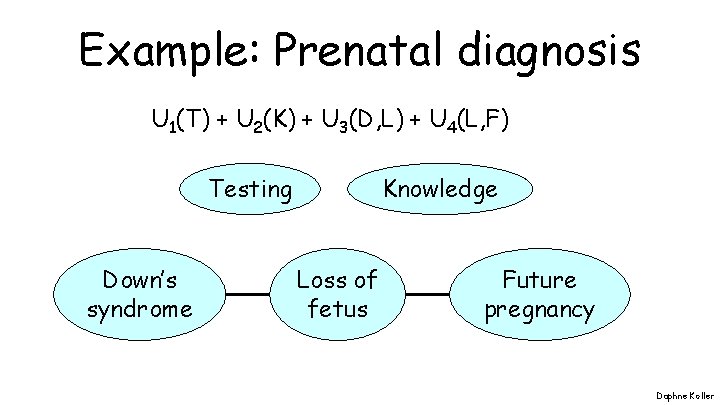
Example: Prenatal diagnosis U 1(T) + U 2(K) + U 3(D, L) + U 4(L, F) Testing Down’s syndrome Knowledge Loss of fetus Future pregnancy Daphne Koller

Summary • Our utility function determines our preferences about decisions that involve uncertainty • Utility generally depends on multiple factors – Money, time, chances of death, … • Relationship is usually nonlinear – Shape of utility curve determines attitude to risk • Multi-attribute utilities can help decompose highdimensional function into tractable pieces Daphne Koller

END END Daphne Koller