Probabilistic Design Introduction An Example Motivation Features Benefits

Probabilistic Design • • Introduction An Example Motivation Features Benefits Probabilistic Methods Probabilistic Results/Interpretation Summary

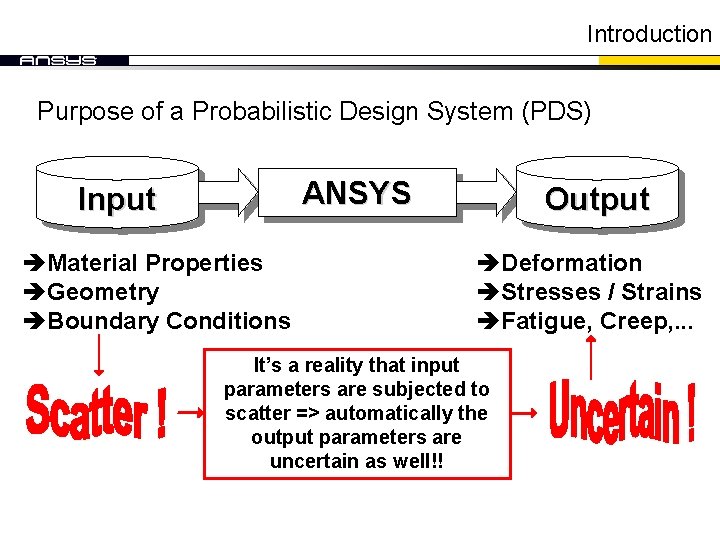
Introduction Purpose of a Probabilistic Design System (PDS) ANSYS Input èMaterial Properties èGeometry èBoundary Conditions Output èDeformation èStresses / Strains èFatigue, Creep, . . . It’s a reality that input parameters are subjected to scatter => automatically the output parameters are uncertain as well!!

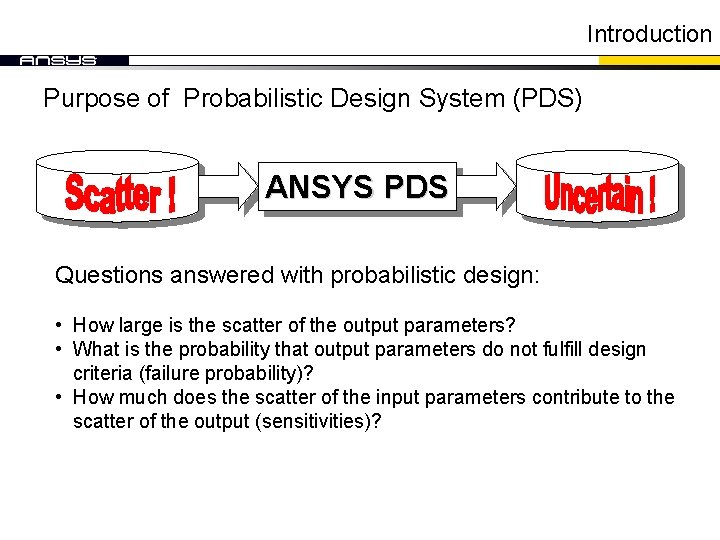
Introduction Purpose of Probabilistic Design System (PDS) ANSYS PDS Questions answered with probabilistic design: • How large is the scatter of the output parameters? • What is the probability that output parameters do not fulfill design criteria (failure probability)? • How much does the scatter of the input parameters contribute to the scatter of the output (sensitivities)?

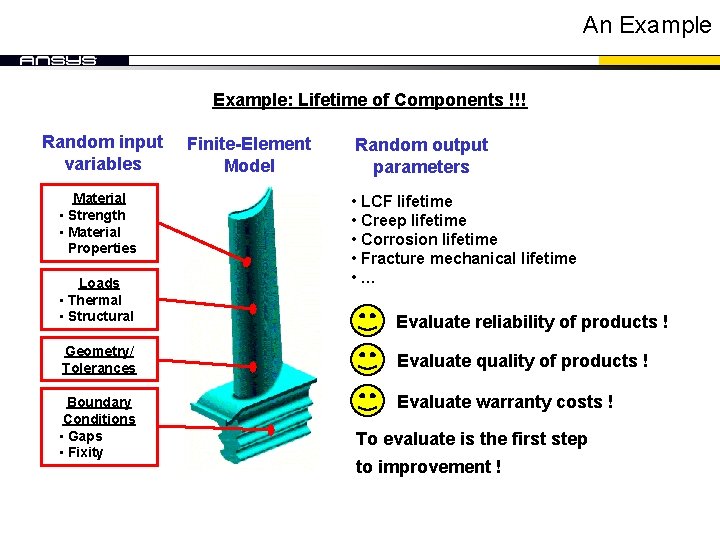
An Example: Lifetime of Components !!! Random input variables Material • Strength • Material Properties Loads • Thermal • Structural Geometry/ Tolerances Boundary Conditions • Gaps • Fixity Finite-Element Model Random output parameters • LCF lifetime • Creep lifetime • Corrosion lifetime • Fracture mechanical lifetime • … Evaluate reliability of products ! Evaluate quality of products ! Evaluate warranty costs ! To evaluate is the first step to improvement !

Motivation Influence of Young’s Modulus and Thermal Expansion Coefficient on thermal stresses: thermal = E · · T Deterministic Approach: Emean and mean => evaluate expected value: expect Probabilistic Approach: ‘E’ scatters ± 5% ‘E’ and ‘ ‘ scatter ± 5% P( thermal > 1. 05 expect) 16% (~1 out of 6) 22% (~1 out of 5) P( thermal > 1. 10 expect) 2. 3% (~1 out of 40) 8% (~1 out of 12)

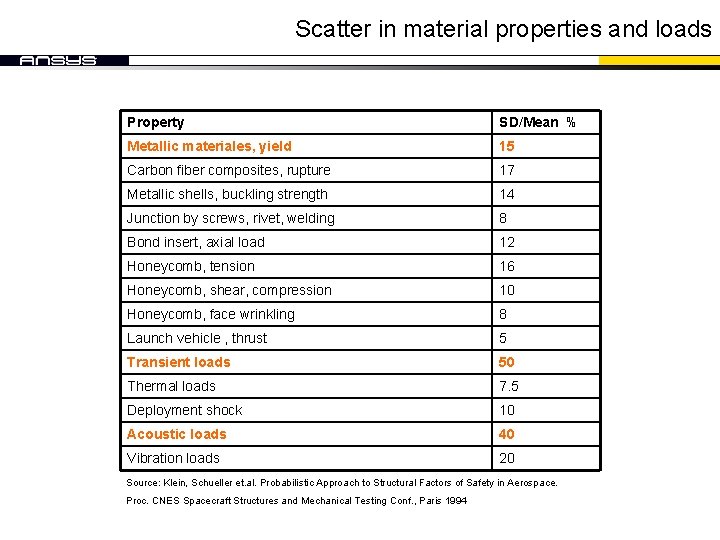
Scatter in material properties and loads Property SD/Mean % Metallic materiales, yield 15 Carbon fiber composites, rupture 17 Metallic shells, buckling strength 14 Junction by screws, rivet, welding 8 Bond insert, axial load 12 Honeycomb, tension 16 Honeycomb, shear, compression 10 Honeycomb, face wrinkling 8 Launch vehicle , thrust 5 Transient loads 50 Thermal loads 7. 5 Deployment shock 10 Acoustic loads 40 Vibration loads 20 Source: Klein, Schueller et. al. Probabilistic Approach to Structural Factors of Safety in Aerospace. Proc. CNES Spacecraft Structures and Mechanical Testing Conf. , Paris 1994

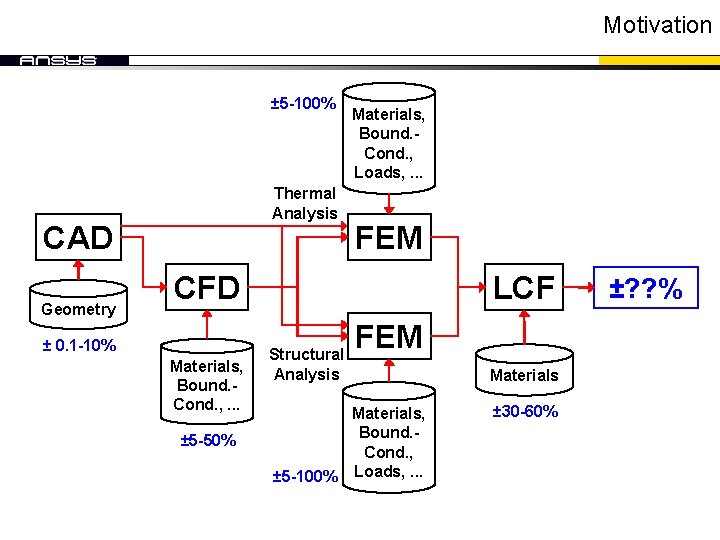
Motivation ± 5 -100% Thermal Analysis CAD Geometry Materials, Bound. Cond. , Loads, . . . FEM CFD ± 0. 1 -10% Materials, Bound. Cond. , . . . ± 5 -50% LCF Structural Analysis FEM Materials, Bound. Cond. , ± 5 -100% Loads, . . . Materials ± 30 -60% ±? ? %

PDS Benefits Deterministic Analysis: • Only provides a YES/NO answer • Safety margins are piled up “blindly” (worst material, maximum load, … worst case) 1 worst case assumption =10 -2 2 worst case assumptions =10 -4 3 worst case assumptions =10 -6 4 worst case assumptions =10 -8. . . => Leads to costly over-design • Only “as planned“, “as is” or the worst design Probabilistic Analysis: • Provides a probability and reliability (design for reliability) • Takes uncertainties into account in a realistic fashion => This is closer to reality => Over-design is avoided • “Tolerance stack-up” is included (design for manufacturability)

PDS Benefits Deterministic Analysis: Probabilistic Analysis: • Sensitivities do not take range of scatter or possibilities into account • Range/width of scatter is “built-in” into probabilistic sensitivities • Sensitivities do not take interactions between input variables into account (second order cross terms) • Interactions between input variables are inherently taken care of • Quality is “indirectly” affected • Quality becomes a measurable, quantifiable and controllable quantity

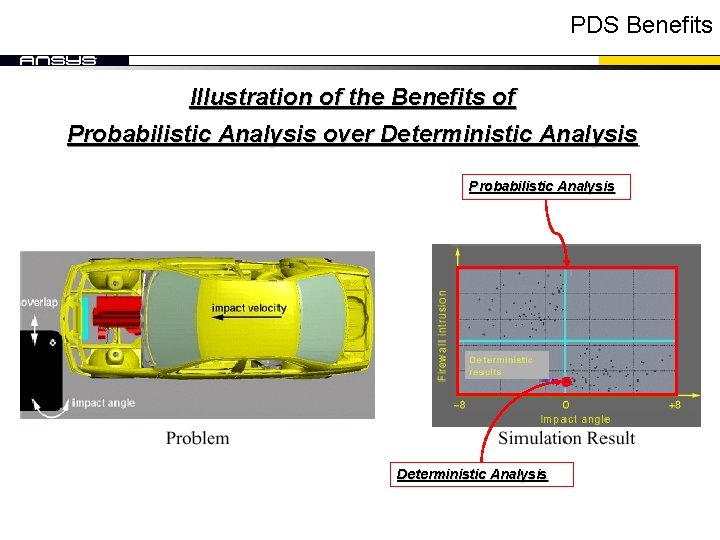
PDS Benefits Illustration of the Benefits of Probabilistic Analysis over Deterministic Analysis Probabilistic Analysis Deterministic Analysis

Features of the ANSYS/Probabilistic Design System • Free for ANSYS users (included in ANSYS since rel. 5. 7) • Works with any ANSYS analysis model • Static, dynamic, linear, non-linear, thermal, structural, electromagnetic, CFD. . • Allows large number random input and output parameters • 10 statistical distributions for random input parameters • Random input parameters can be correlated • Probabilistic methods: • Monte Carlo - Direct & Latin Hypercube Sampling • Response Surface - Central Composite & Box-Behnken Designs

Features of the ANSYS/Probabilistic Design System • Use of distributed, parallel computing techniques for drastically reduced wall clock time • Comprehensive probabilistic results • Convergence plots, histogram, probabilities, scatter plots, sensitivities, . . . • State-of-the art statistical procedures to address the accuracy of the output data • Confidence intervals

Features of the ANSYS/Probabilistic Design System ANSYS Customer Base • All “Top 10” Fortune 100 Industrial companies • 73 of the Fortune 100 Industrial companies • Over 5, 700 commercial companies • Over 40, 000 commercial customer seats • Over 100, 000 university licenses Probabilistic Design • Available since ANSYS 5. 7 and after • Used by well over 100 companies in production

Monte Carlo Simulation: Perform numerous analysis runs based on sets of random samples, and then evaluate statistics of derived responses. • Direct (Crude) Sampling Monte Carlo (DIR) • Latin Hypercube Sampling Monte Carlo (LHS) • User defined (USR) Fully Parallel Probabilistic Methods

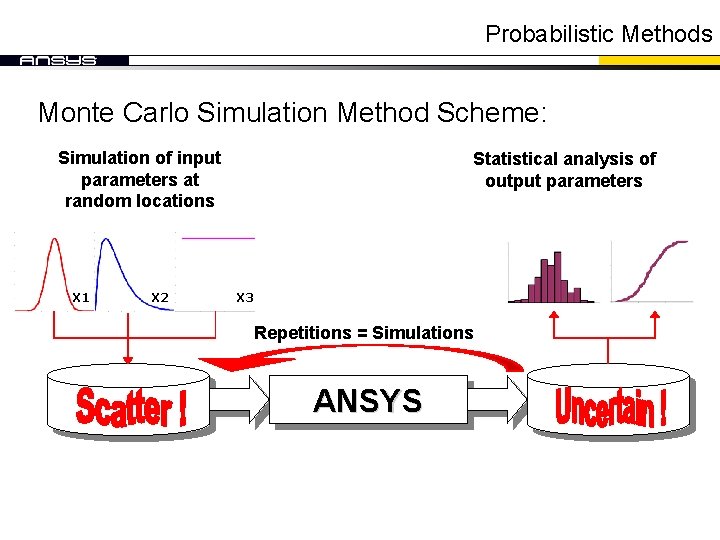
Probabilistic Methods Monte Carlo Simulation Method Scheme: Simulation of input parameters at random locations X 1 X 2 Statistical analysis of output parameters X 3 Repetitions = Simulations ANSYS

Probabilistic Methods Finite Element Runs for Monte Carlo For Monte Carlo Simulation the number of simulations does not depend on the number of random input variables, but on the probabilistic result you are looking for: • For assessment of the statistics of output parameters (Mean, sigma) Nsim 30 … 100 • For histogram and cumulative distribution function Nsim 50 … 200 • For assessment of low probabilities P (tails of the distribution) Nsim 30/P … 100/P

– Response Surface Methods: Select specific observation points for each random variable, run analyses, establish response surface for each response parameter, perform Monte Carlo Analysis on Response Surface. • Central Composite Design (CCD) • Box-Behnken Matrix (BBM) • User defined (USR) Fully Parallel Probabilistic Methods

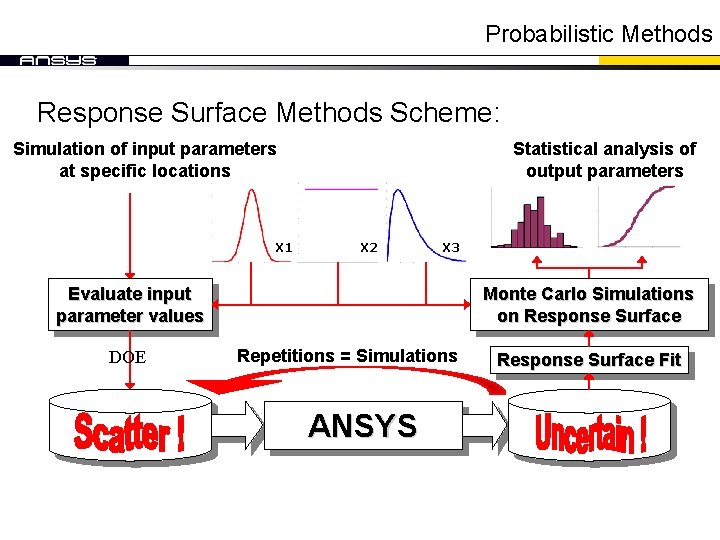
Probabilistic Methods Response Surface Methods Scheme: Simulation of input parameters at specific locations X 1 Statistical analysis of output parameters X 2 X 3 Evaluate input parameter values DOE Monte Carlo Simulations on Response Surface Repetitions = Simulations ANSYS Response Surface Fit

Probabilistic Methods Finite Element Runs for Response Surface For Response Surface Methods the number of simulations depends on the number of random input variables only : No. of random input variables 1 2 3 4 5 6 7 8 9 10 . . . Coefficients of equation 3 6 10 15 21 28 36 45 55 66 Central Compos. Box. Behnken 9 15 25 27 45 79 81 147 149 13 25 41 49 57 65 121 161

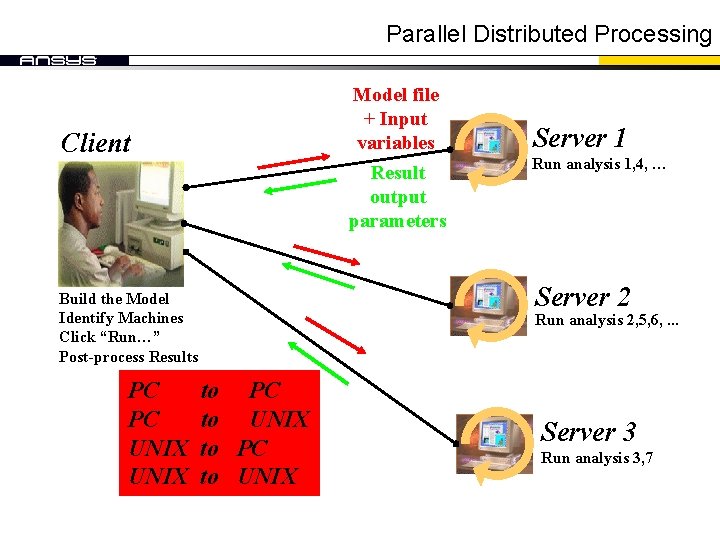
Parallel Distributed Processing Model file + Input variables Client Result output parameters Run analysis 1, 4, … Server 2 Build the Model Identify Machines Click “Run…” Post-process Results PC PC UNIX Server 1 Run analysis 2, 5, 6, . . . to PC to UNIX Server 3 Run analysis 3, 7

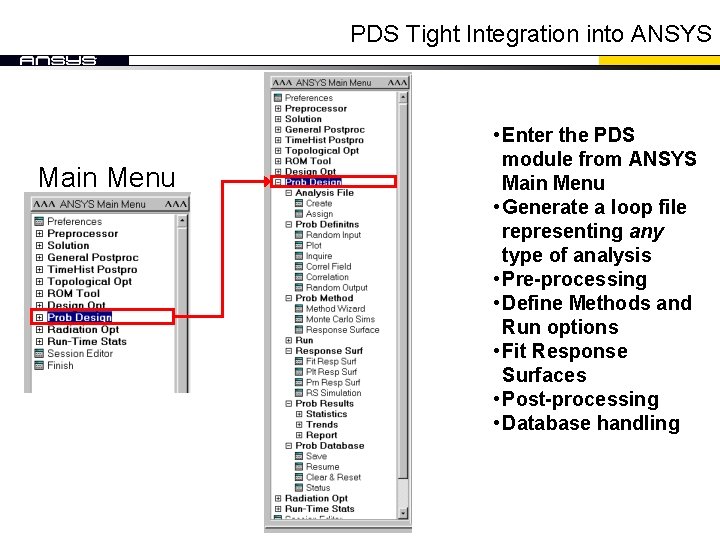
PDS Tight Integration into ANSYS Main Menu • Enter the PDS module from ANSYS Main Menu • Generate a loop file representing any type of analysis • Pre-processing • Define Methods and Run options • Fit Response Surfaces • Post-processing • Database handling

Probabilistic Results Post-processing of simulations results: The results should be displayed such that the user can graphically and intuitively answer the questions: 1 How large is the scatter of the output parameters? Plot: Statistics (sigma), Histogram, Sample Diagrams 2 What is the probability that output parameters do not fulfil design criteria (failure probability)? Plot: Cumulative Distribution Function, Probabilities 3 How much does the scatter of the input parameters contribute to the scatter of the output? Plot: Sensitivities, Scatter Diagram, Response Surface

Probabilistic Results Simulation Value Sample Plot:

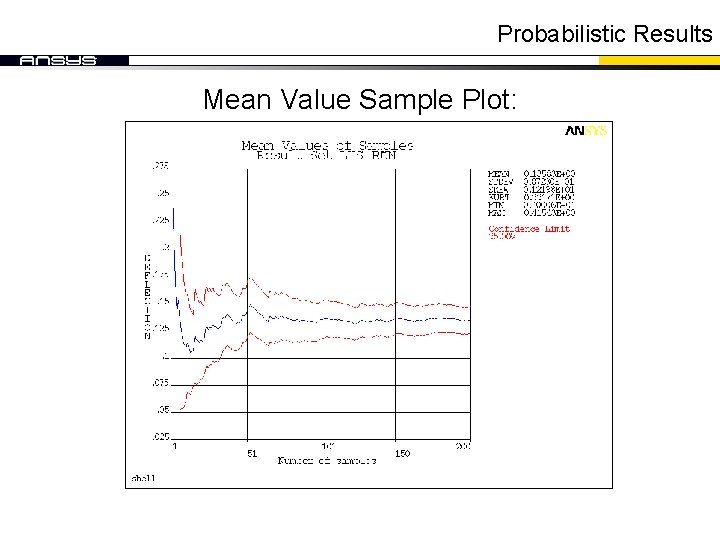
Probabilistic Results Mean Value Sample Plot:

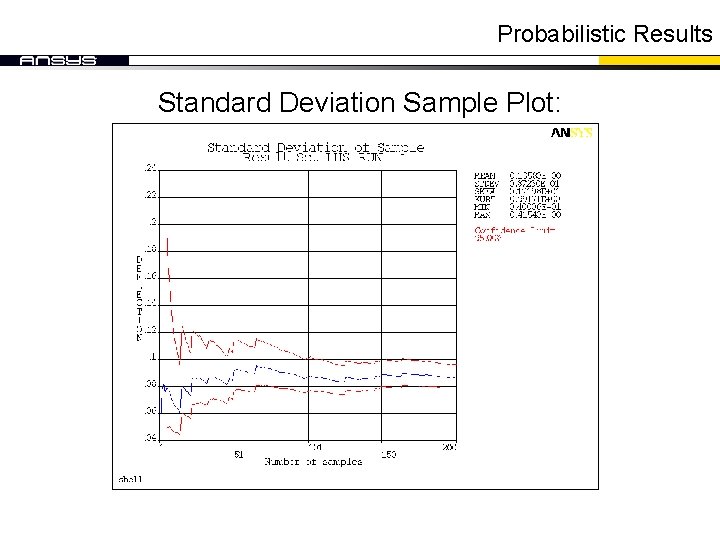
Probabilistic Results Standard Deviation Sample Plot:

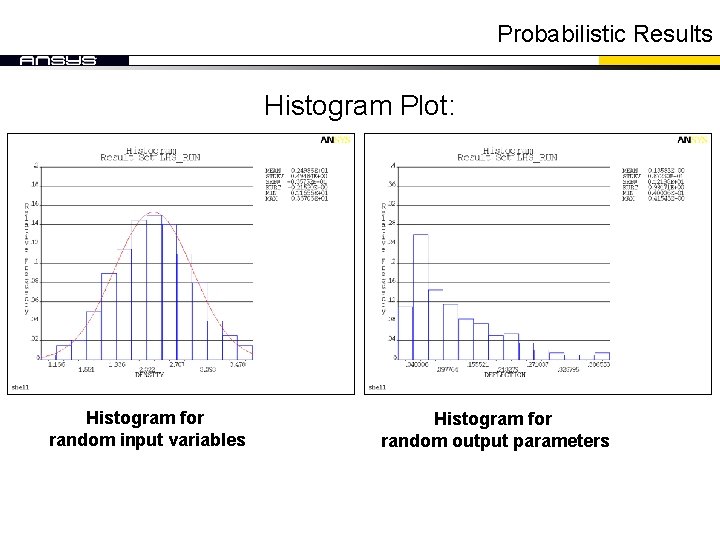
Probabilistic Results Histogram Plot: Histogram for random input variables Histogram for random output parameters

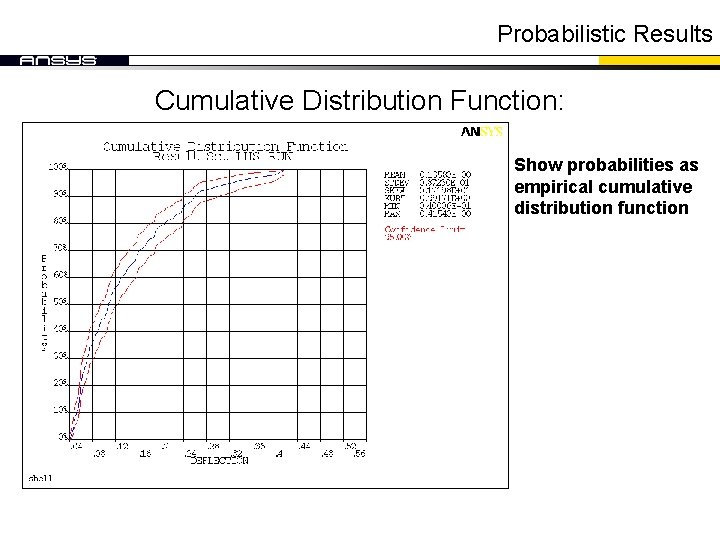
Probabilistic Results Cumulative Distribution Function: Show probabilities as empirical cumulative distribution function

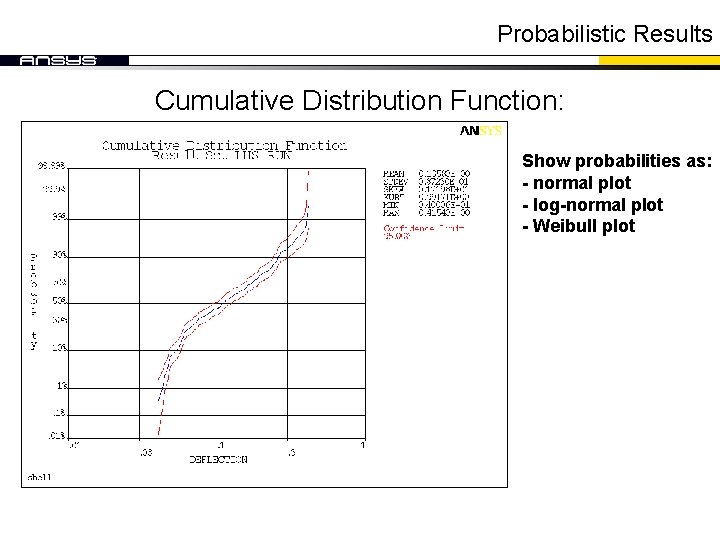
Probabilistic Results Cumulative Distribution Function: Show probabilities as: - normal plot - log-normal plot - Weibull plot

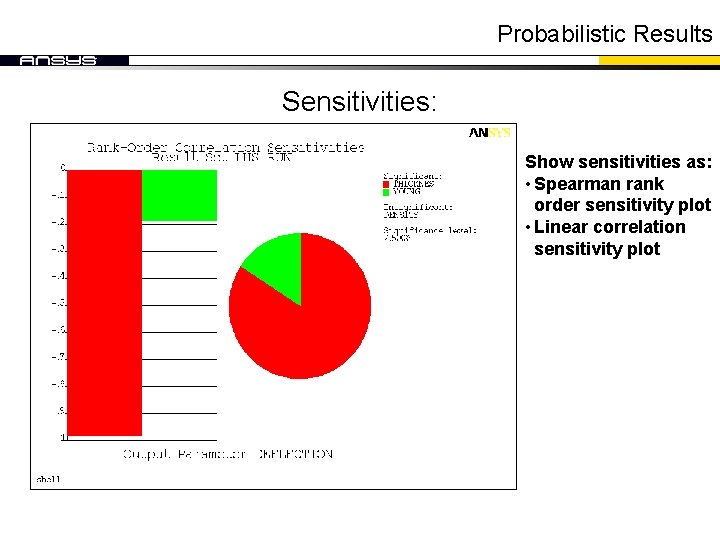
Probabilistic Results Sensitivities: Show sensitivities as: • Spearman rank order sensitivity plot • Linear correlation sensitivity plot

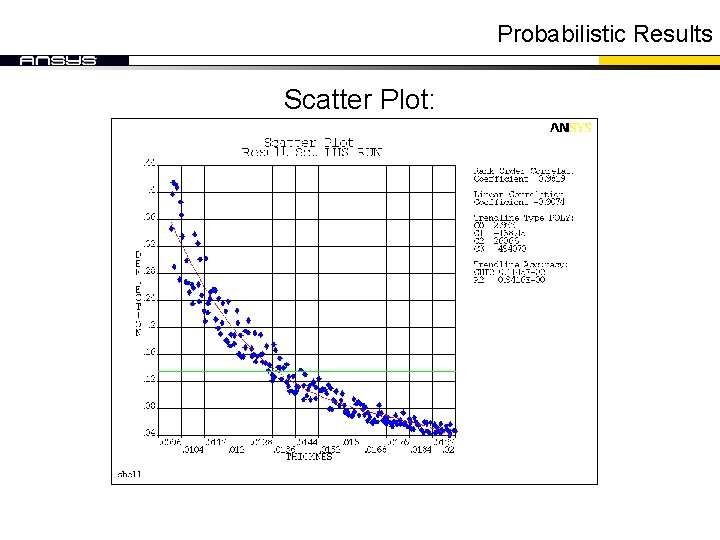
Probabilistic Results Scatter Plot:

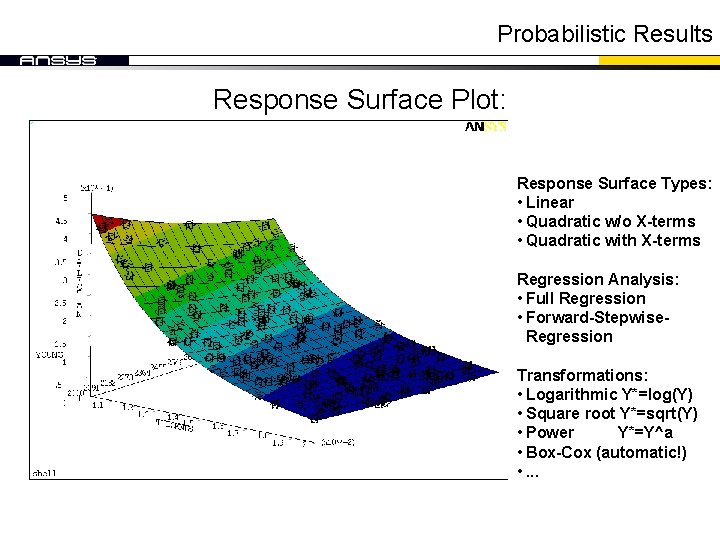
Probabilistic Results Response Surface Plot: Response Surface Types: • Linear • Quadratic w/o X-terms • Quadratic with X-terms Regression Analysis: • Full Regression • Forward-Stepwise. Regression Transformations: • Logarithmic Y*=log(Y) • Square root Y*=sqrt(Y) • Power Y*=Y^a • Box-Cox (automatic!) • . . .

Probabilistic Results Sharing HTML Report: Note: • Report is automatically generated (pushbutton) • It includes all pictures according to user preferences/options • It includes explanations as text Click to see Report

Summary • Deterministic engineering design practices have matured and do not yield significant performance gains. • Future design improvements will require accounting for variations. • Probabilistic approach enables Design for Quality, Reliability and Robustness • Reduced warranty costs • Better resale value • Increased market size, market share, and margin on sales • Distributed computing allows faster simulation turn-around