Probabilistic Data Management Chapter 2 Data Uncertainty Model

Probabilistic Data Management Chapter 2: Data Uncertainty Model

Objectives n In this chapter, you will: q q q Learn the formal definition of uncertain data Explore different granularities of data uncertainty Become familiar with different representations of uncertain data Become aware of possible worlds semantics Learn the representations of correlations over uncertain data 2

Outline n n n Introduction Uncertain Data Model Possible Worlds Correlated Uncertain Data Summary 3

Introduction n In real-world applications, uncertain data are of various types q Numerical data n n n q Sensory data GPS data Medical data Categorical data n Text data 4

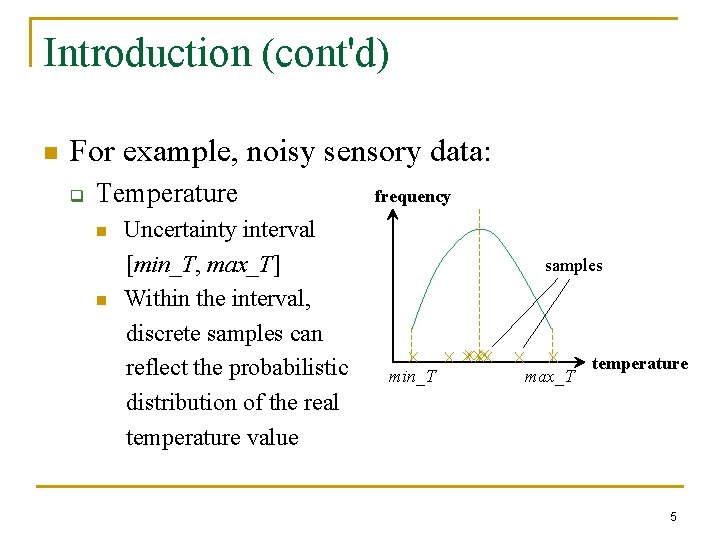
Introduction (cont'd) n For example, noisy sensory data: q Temperature n n Uncertainty interval [min_T, max_T] Within the interval, discrete samples can reflect the probabilistic distribution of the real temperature value frequency samples min_T max_T temperature 5

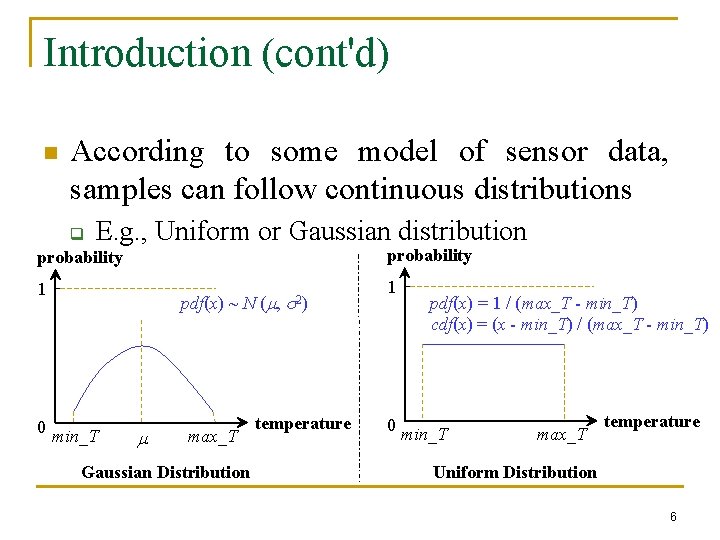
Introduction (cont'd) n According to some model of sensor data, samples can follow continuous distributions E. g. , Uniform or Gaussian distribution q probability 1 0 pdf(x) ~ N (m, s min_T m max_T Gaussian Distribution 2) temperature 1 0 pdf(x) = 1 / (max_T - min_T) cdf(x) = (x - min_T) / (max_T - min_T) min_T max_T temperature Uniform Distribution 6

Outline n n n Introduction Uncertain Data Model Possible Worlds Correlated Uncertain Data Summary 7

In the Last Chapter: Classification of Person ID Zip code Disease Data Uncertainty (110000, 0. 5), (pneumonia, 0. 3), n Granularity q Attribute Uncertainty n q PID 1 (110001, 0. 5) (flu, 0. 7) PID 2 (310000, 1) (AIDS, 0. 9) Each attribute of a tuple has several possible values (associated with probabilities) Tuple Uncertainty n Each tuple is associated with an existence probability Witnessed Person t. p PID 1 0. 9 PID 2 0. 2 PID 3 0. 1 8

Attribute-Level Uncertain Data n Uncertain object in uncertain databases q q q Each uncertain object o is represented by an uncertainty region, UR(o) Within the uncertainty region, object o can appear anywhere following any distribution The object distribution can be represented by either discrete samples or continuous probabilistic distribution uncertainty region 9

Attribute-Level Uncertain Data (cont'd) n The shape of the uncertainty region can be arbitrary q q Irregular shape Regular shape n n Hypersphere Hyperrectangle 10

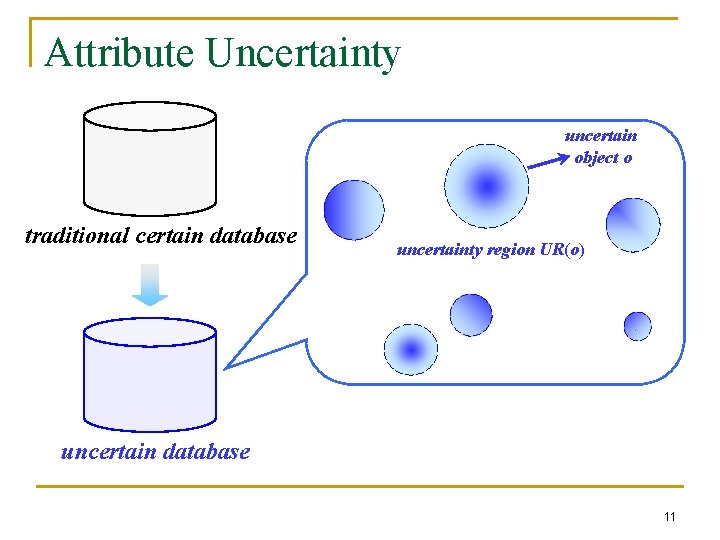
Attribute Uncertainty uncertain object o traditional certain database uncertainty region UR(o) uncertain database 11

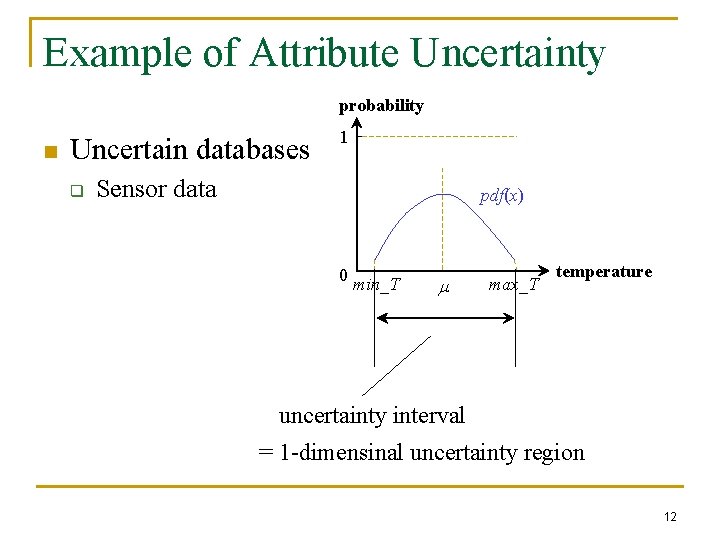
Example of Attribute Uncertainty probability n Uncertain databases q 1 Sensor data pdf(x) 0 min_T m max_T temperature uncertainty interval = 1 -dimensinal uncertainty region 12

Tuple Uncertainty n Block independent disjoint model q A probabilistic database contains a set of x-tuples ti n n q Each x-tuple represents a data entity x-tuples are independent of each other Each x-tuple ti has one or multiple alternatives tij n n n Each alternative tij represents one possible instance of the data entity ti that may appear in reality Each alternative tij is associated with an existence probability tij. p, such that ∑ j tij. p ≤ 1 Alternatives in the same x-tuple are mutually exclusive 13

Example of Tuple Uncertainty n Probabilistic databases q x-tuples n n q Person ID Witness ID Location Prob. a a 1 X 0. 5 a a 2 Y 0. 4 b b Z 0. 8 1 Person IDs a and b probabilistic database a and b are independent of each other Alternatives n n n Person ID a: a 1, a 2 Person ID b: b 1 Each person (e. g. , a) has at most one possible instance (witness person a 1 or a 2) appearing in reality (i. e. , to be true) 14

Outline n n n Introduction Uncertain Data Model Possible Worlds Correlated Uncertain Data Summary 15

Example of Possible Worlds n Previous example q q q In reality, each person, a or b, can be located at one place at a timestamp Thus, for each person ID, at most one witness tuple is true Person Witness Location Prob. ID ID E. g. , a 1 and b 1 a a 1 X 0. 5 a a 2 Y 0. 4 b b 1 Z 0. 8 probabilistic database 16

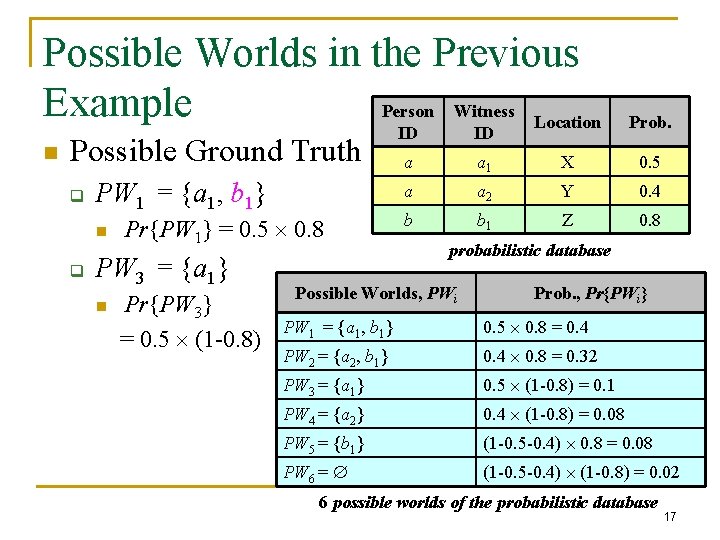
Possible Worlds in the Previous Example Person Witness Location n Possible Ground Truth q PW 1 = {a 1, b 1} n q Pr{PW 1} = 0. 5 0. 8 PW 3 = {a 1} n Pr{PW 3} = 0. 5 (1 -0. 8) Prob. ID ID a a 1 X 0. 5 a a 2 Y 0. 4 b b 1 Z 0. 8 probabilistic database Possible Worlds, PWi Prob. , Pr{PWi} PW 1 = {a 1, b 1} 0. 5 0. 8 = 0. 4 PW 2 = {a 2, b 1} 0. 4 0. 8 = 0. 32 PW 3 = {a 1} 0. 5 (1 -0. 8) = 0. 1 PW 4 = {a 2} 0. 4 (1 -0. 8) = 0. 08 PW 5 = {b 1} (1 -0. 5 -0. 4) 0. 8 = 0. 08 PW 6 = (1 -0. 5 -0. 4) (1 -0. 8) = 0. 02 6 possible worlds of the probabilistic database 17

Possible Worlds Semantics n In the probabilistic database D, q q q Person ID Witness ID Location Prob. a a 1 X 0. 5 a a 2 Y 0. 4 b b 1 Z 0. 8 A possible world is a materialized instance of the database that can appear in the real world Each x-tuple contributes at most one alternative to the possible world Each possible world, pw(D), is associated with an appearance probability, Pr{pw(D)}, indicating the chance that the possible world appears in the real world 18

Possible Worlds on Attribute Uncertainty n Uncertain database q q In a possible world, each uncertain object contributes one possible instance within the uncertainty region The probability of the possible world is given by the multiplication of instance existence probability uncertain object o uncertainty region UR(o) 19

Comments on Possible Worlds In uncertain/probabilistic databases, there can be exponential number of possible worlds w. r. t. database size n Possible world semantics is a natural interpretation of uncertain/probabilistic databases n Query processing under possible worlds semantics is rather costly, and efficient approaches have to be proposed n 20

Exercises x-tuple ti t 1 t 2 Alt. tij Attr. Prob. t 11 4 0. 3 t 12 5 0. 4 t 21 2 0. 7 1. How many possible t 31 11 0. 6 worlds are there in the t 32 15 0. 3 t 33 12 0. 1 probabilistic database? 2. Is {t 11, t 21, t 33} a possible world? Why? What is its appearance probability? 3. Is {t 11, t 33} a possible world? Why? What is its appearance probability? 4. Is {t 21} a possible world? Why? What is its appearance probability? 5. Is a possible world? Why? What is its appearance probability? 21

Outline n n n Introduction Uncertain Data Model Possible Worlds Correlated Uncertain Data Summary 22

In the Last Chapter: Classification of Data Uncertainty n Correlations q Independent Uncertainty n n q Correlated Uncertainty n n q Uncertain objects are independent of each other E. g. , uncertain databases, probabilistic databases Attributes of uncertain objects are correlated with each other E. g. , Bayesian network Uncertainty with Local Correlations n n Uncertain objects from different groups are independent Within each group, uncertain objects are locally correlated 23

Applications of Correlated Uncertain Data n Sensor networks q q n Sensory data collected from spatially close sensors are correlated with each other E. g. , temperature collected from sensors within 1 meter Data integration q q q Data sources may copy from each other Errors and impreciseness may be propagated Thus, uncertain data from different sources can be correlated 24

Model for Correlated Uncertain Data n Graphical Data Model q Directed graph n n q Markovian model Bayesian network Undirected graph n Conditional random fields 25

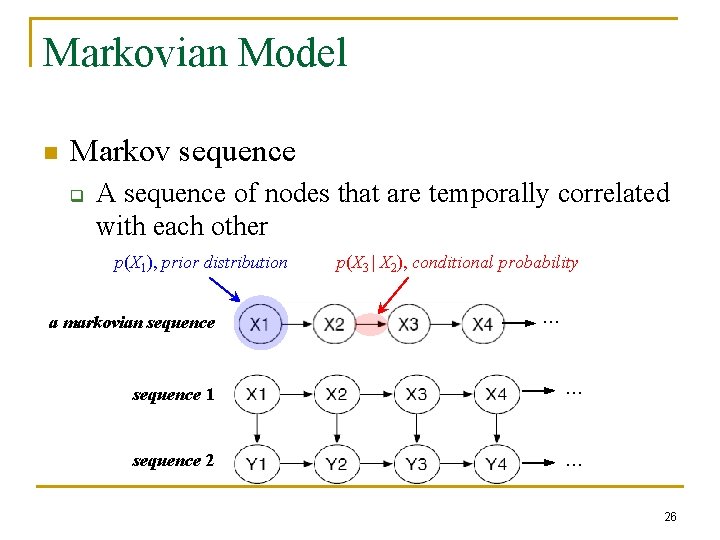
Markovian Model n Markov sequence q A sequence of nodes that are temporally correlated with each other p(X 1), prior distribution a markovian sequence p(X 3 | X 2), conditional probability … sequence 1 … sequence 2 … 26

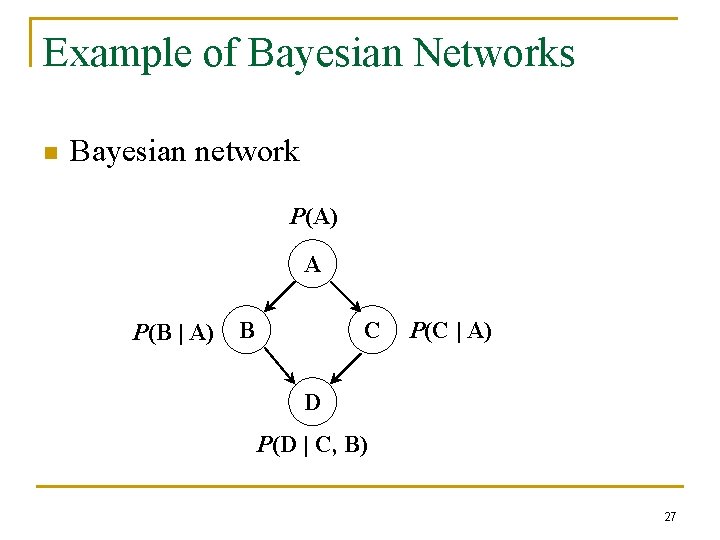
Example of Bayesian Networks n Bayesian network P(A) A P(B | A) B C P(C | A) D P(D | C, B) 27

Bayesian Networks n Bayesian network q q q n Vertices: random variables Directed edges: indicating the dependency between two random variables Conditional probability tables (CPTs): storing prior/conditional probabilities of labels in vertices Possible worlds q Each label assignment to graph corresponds to one possible world vertices 28

Variable Elimination How do we compute P(X 2)? Bayes' formula X 1 X 2 29

Variable Elimination (cont'd) X 1 X 2 X 3 n How do we compute P(X 3)? n We already know how to compute P(X 2). . . 30

Variable Elimination (cont'd) T S V L B A n P(V, S, T, L, A, B, X, D) X D Eliminate: v Compute: 31

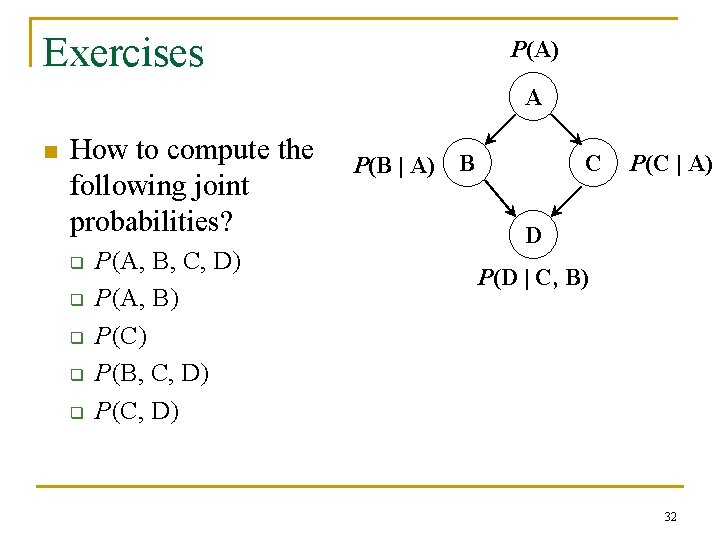
Exercises P(A) A n How to compute the following joint probabilities? q q q P(A, B, C, D) P(A, B) P(C) P(B, C, D) P(B | A) B C P(C | A) D P(D | C, B) 32

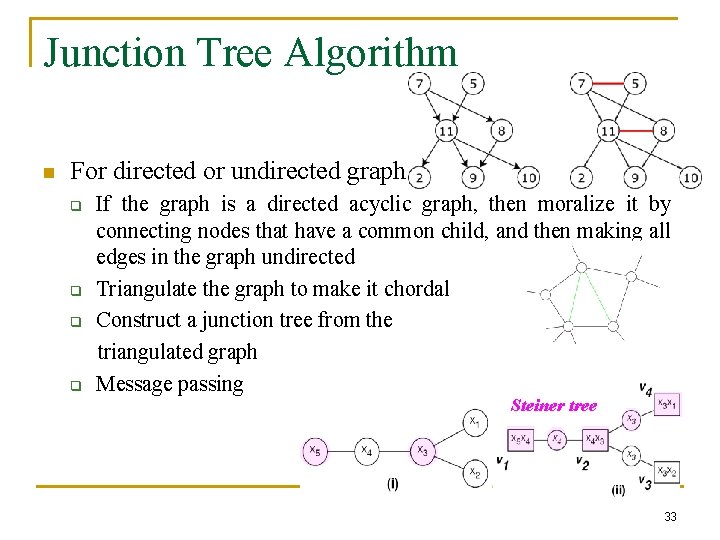
Junction Tree Algorithm n For directed or undirected graph q q If the graph is a directed acyclic graph, then moralize it by connecting nodes that have a common child, and then making all edges in the graph undirected Triangulate the graph to make it chordal Construct a junction tree from the triangulated graph Message passing Steiner tree 33

Undirected Graphical Model n Provided then joint distribution is product of non-negative functions over the cliques of the graph where are the clique potentials, and Z is a normalization constant 34

Undirected Graphical Model (cont'd) n n A graph G=(Y, E) where Y={y 1, y 2, …, yn} are the nodes (vertices) and E={( yi , yj ): i ≠ j} are the undirected edges. The probability distribution is given as: , such that, potential function where c are the cliques in the graph and Z is the partition function defined as: 35

Conditional Random Field (CRF) n n Nodes in Y = {y 1, y 2, …, yn} correspond to hidden (or unknown) states Given some observation X={x 1, x 2, …, xn}, we may want to infer states of xi according to conditional probability Pr{Y | X} q Parameters in Pr{Y | X} are learnt from training data 36

Uncertainty With Local Correlations n In many applications, data are locally correlated q Sensor networks n n Spatially close sensors report correlated data Sensors far away from each other usually report independent data 37

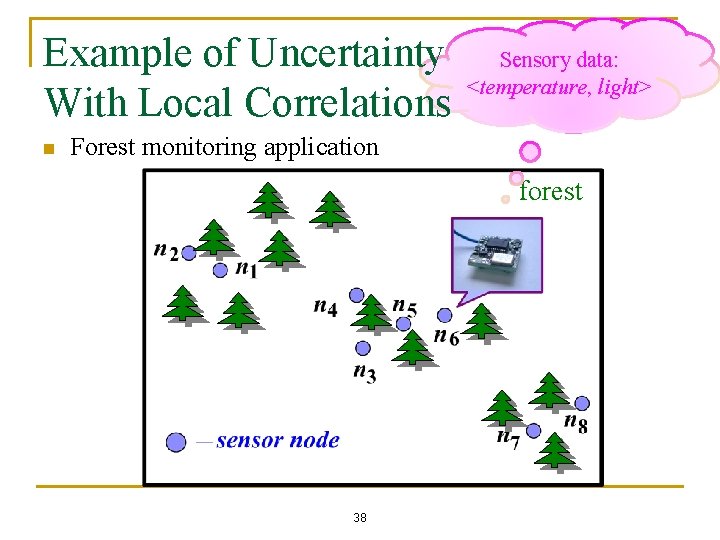
Example of Uncertainty With Local Correlations n Sensory data: <temperature, light> Forest monitoring application forest 38

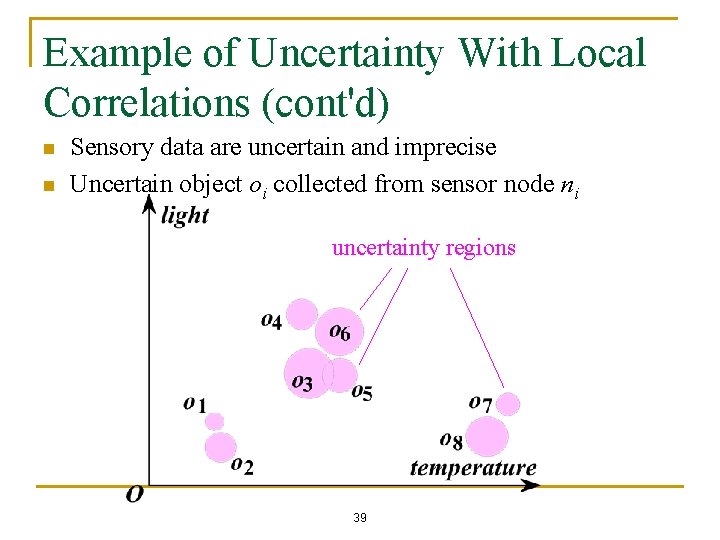
Example of Uncertainty With Local Correlations (cont'd) n n Sensory data are uncertain and imprecise Uncertain object oi collected from sensor node ni uncertainty regions 39

Example of Uncertainty With Local Correlations (cont'd) n 3 monitoring areas forest 40

Example of Uncertainty With Local Correlations (cont'd) n 3 monitoring areas forest sensors far away spatially close sensors 41

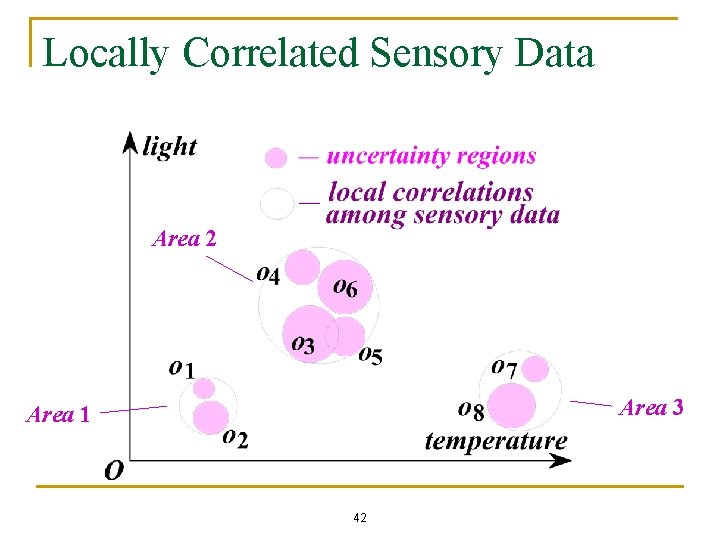
Locally Correlated Sensory Data Area 2 Area 3 Area 1 42

Data Model for Local Correlations n Data Model q Each uncertain object contains several locally correlated partitions (LCPs) n n Uncertain objects within each LCP are correlated with each other Uncertain objects from distinct LCPs are independent of each other 43

Data Model for Local Correlations (cont'd) n Bayesian network q q Each vertex corresponds to a random variable Each vertex is associated with a conditional probability table (CPT) 44

Data Model for Local Correlations (cont'd) n The joint probability of variables q q Join tuples in CPTs and multiply conditional probabilities Variable elimination 45

Outline n n n Introduction Uncertain Data Model Possible Worlds Correlated Uncertain Data Summary 46

Summary n n In different real applications, data uncertainty can have different representations Attribute uncertainty vs. tuple uncertainty q q n Uncertain databases (spatial representation) Probabilistic database (relational representation) Possible worlds semantics q A possible instance of the database that can appear in the real world 47

Summary (cont'd) n Correlated uncertainty q Graphical model n n n q Calculation of the joint probability in graphical model n q Markovian model Bayesian network Conditional random fields Junction tree algorithm Uncertainty with local correlations 48