Probabilistic Context Free Grammars Grant Schindler 8803 MDM

Probabilistic Context Free Grammars Grant Schindler 8803 -MDM April 27, 2006

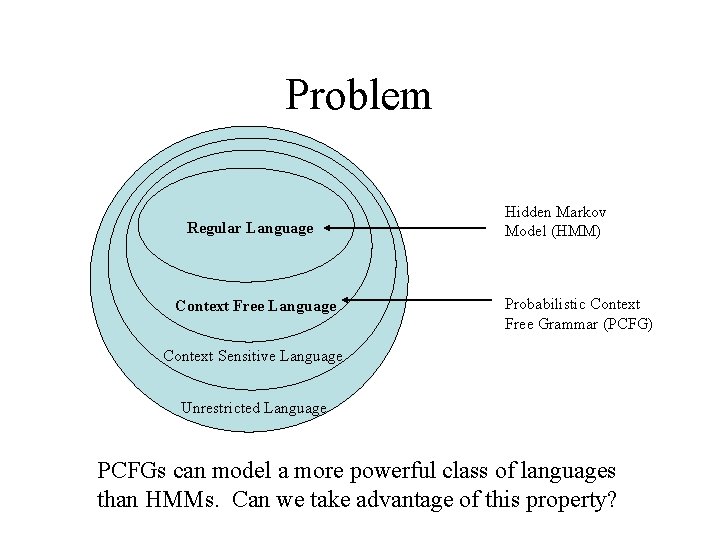
Problem Regular Language Context Free Language Hidden Markov Model (HMM) Probabilistic Context Free Grammar (PCFG) Context Sensitive Language Unrestricted Language PCFGs can model a more powerful class of languages than HMMs. Can we take advantage of this property?

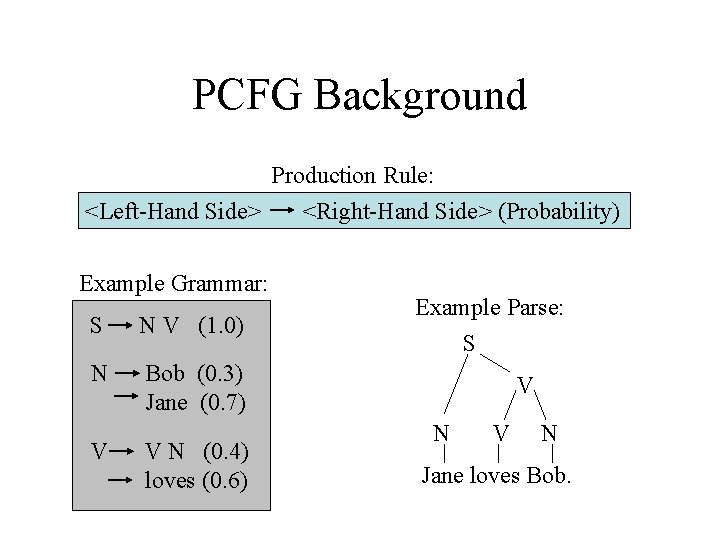
PCFG Background Production Rule: <Left-Hand Side> <Right-Hand Side> (Probability) Example Grammar: S N V (1. 0) N Bob (0. 3) Jane (0. 7) V V N (0. 4) loves (0. 6) Example Parse: S V N Jane loves Bob.

PCFG Applications • Natural Language Processing: parsing written sentences • Bio. Informatics: RNA sequences • Stock Markets: model rise/fall of the Dow Jones (? ) • Computer Vision: parsing architectural scenes

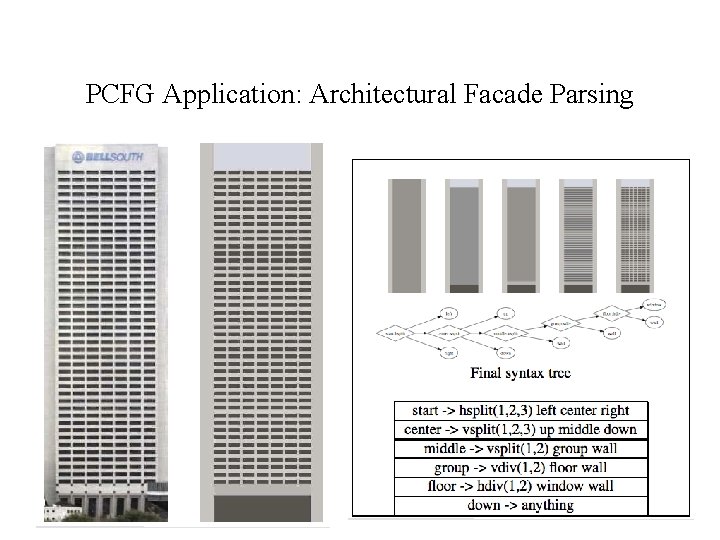
PCFG Application: Architectural Facade Parsing

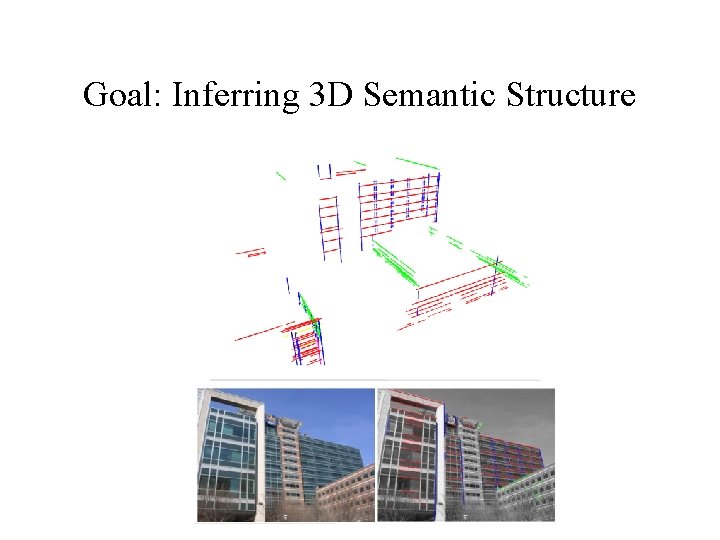
Goal: Inferring 3 D Semantic Structure

Discrete vs. Continuous Observations Discrete Values Continuous Values • Natural Language Processing: parsing written sentences • Bio. Informatics: RNA sequences • Stock Markets: model rise/fall of the Dow Jones (? ) How do we estimate the parameters of PCFGs with continuous observation densities (terminal nodes in the parse tree)?

PCFG Parameter Estimation In the discrete case, there exists an Expectation Maximization (EM) algorithm: E-Step: Compute expected number of times each rule (A-> BC) is used in generating a given set of observation sequences (based on previous parameter estimates). M-Step: Update parameters as normalized counts computed in E-Step. Essentially: P*(N Bob) = #Bobs / #Nouns

Gaussian Parameter Update Equations NEW! Probability that rule A was applied to generate the observed value at location i, computed from Inside-Outside Algorithm via CYK Algorithm

Significance We can now begin applying probabilistic context-free grammars to problems with continuous data (e. g. stock market) rather than restricting ourselves to discrete outputs (e. g. natural language, RNA). We hope to find problems for which PCFGs offer a better model than HMMs.

Questions

Open Problems How do we estimate the parameters of PCFGs with: A. continuous observation densities (terminal nodes in the parse tree)? B. continuous values for both non-terminal and terminal nodes?

CYK Algorithm Inside-Outside Probabilities