Probabilidad Condicional y Bayes Ing Ral Alvarez Guale

Probabilidad Condicional y Bayes Ing. Raúl Alvarez Guale, MPC

Población •

Ejemplo 1: Probabilidad Condicional Si la probabilidad de que un sistema de comunicación tendrá alta fidelidad es 0. 81, así como la probabilidad de que tendrá alta fidelidad y alta selectividad es 0. 18. ¿cuál es la probabilidad de que un sistema con alta fidelidad también tendrá alta selectividad?

Ejemplo 1: Probabilidad Condicional •

TEOREMA •

Ejemplo: Eventos Independientes ¿Cuál es la probabilidad de obtener dos caras en dos lanzamientos de una moneda equilibrada?

Ejemplo: Eventos Independientes •

TEOREMA •

TEOREMA DE BAYES •

Ejemplo 1 : Probabilidades condicionales Una empresa produce por medio de sus maquinas A, B, C, en porcentaje de producción correspondiente a 50%, 40% y 10% respectivamente. Los productos en mal estado de las máquinas A, b y C, son 3%, 2% y 1% respectivamente.
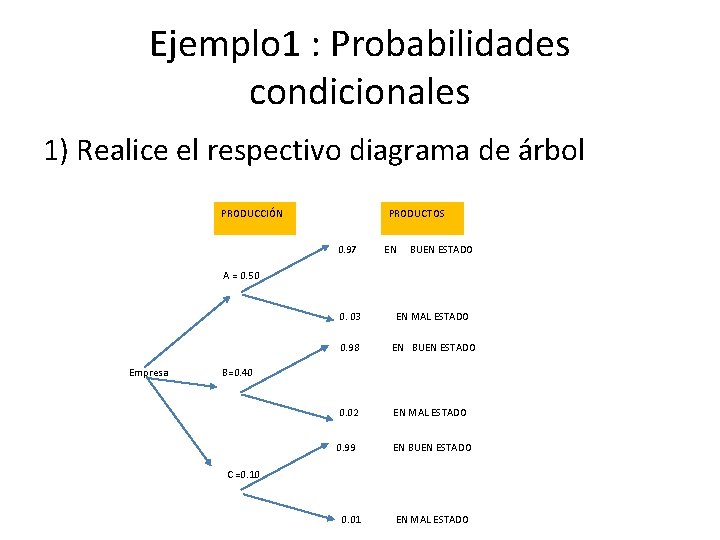
Ejemplo 1 : Probabilidades condicionales 1) Realice el respectivo diagrama de árbol PRODUCCIÓN PRODUCTOS 0. 97 EN BUEN ESTADO A = 0. 50 0. 03 EN MAL ESTADO 0. 98 EN BUEN ESTADO Empresa B=0. 40 0. 02 EN MAL ESTADO 0. 99 EN BUEN ESTADO C =0. 10 0. 01 EN MAL ESTADO

Ejemplo 1 : Probabilidades condicionales 2)¿Cuál es la probabilidad de que al escoger un producto al azar, este se encuentre en mal estado? Solución 1 : Se separan los eventos condicionales de las hojas y se multiplican por sus ramificaciones considerando los espacios muestrales
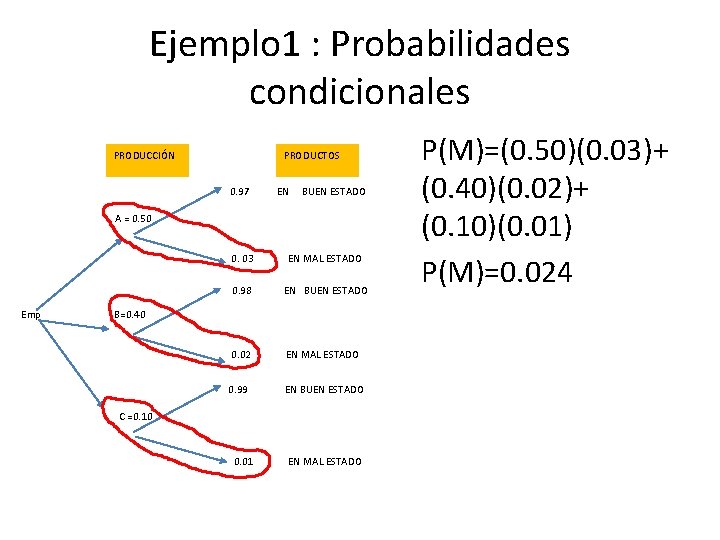
Ejemplo 1 : Probabilidades condicionales PRODUCCIÓN PRODUCTOS 0. 97 EN BUEN ESTADO A = 0. 50 0. 03 EN MAL ESTADO 0. 98 EN BUEN ESTADO Emp B=0. 40 0. 02 EN MAL ESTADO 0. 99 EN BUEN ESTADO C =0. 10 0. 01 EN MAL ESTADO P(M)=(0. 50)(0. 03)+ (0. 40)(0. 02)+ (0. 10)(0. 01) P(M)=0. 024

Ejemplo 1 : Probabilidades condicionales •

Ejemplo 1 : Probabilidades condicionales •

Ejemplo 1 : Probabilidades condicionales 2)¿Cuál es la probabilidad de que al escoger un producto al azar, este se encuentre en buen estado? Solución 1 : Se separan los eventos condicionales de las hojas y se multiplican por sus ramificaciones considerando los espacios muestrales

Ejemplo 1 : Probabilidades condicionales PRODUCCIÓN PRODUCTOS 0. 97 EN BUEN ESTADO A = 0. 50 0. 03 EN MAL ESTADO 0. 98 EN BUEN ESTADO Emp B=0. 40 0. 02 EN MAL ESTADO 0. 99 EN BUEN ESTADO C =0. 10 0. 01 EN MAL ESTADO P(B)=(0. 50)(0. 97) +(0. 40)(0. 98)+ (0. 10)(0. 99) P(B)=0. 976

Ejemplo 1 : Probabilidades condicionales •

Ejemplo 1 : Probabilidades condicionales •

Ejemplo 1 : Probabilidades condicionales 3) Se escoge un producto al azar, y se nota que se encuentra en buen estado. ¿Cuál es la probabilidad de que es producto haya sido producido por la máquina A?

Ejemplo 1 : Probabilidades condicionales 3) Se escoge un producto al azar, y se nota que se encuentra en buen estado. ¿Cuál es la probabilidad de que es producto haya sido producido por la máquina A? Solución 1: Se separan los eventos condicionales de las hojas y se multiplican por sus ramificaciones considerando los espacios muestrales
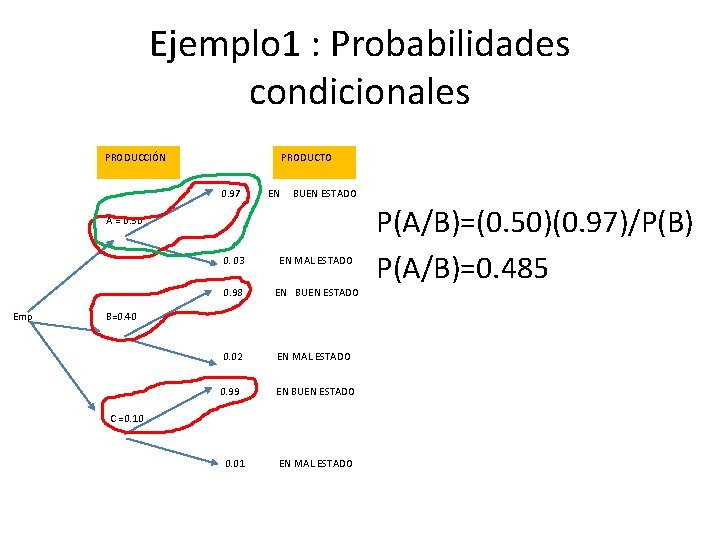
Ejemplo 1 : Probabilidades condicionales PRODUCCIÓN PRODUCTO 0. 97 EN BUEN ESTADO A = 0. 50 0. 03 EN MAL ESTADO 0. 98 EN BUEN ESTADO Emp B=0. 40 0. 02 EN MAL ESTADO 0. 99 EN BUEN ESTADO C =0. 10 0. 01 EN MAL ESTADO P(A/B)=(0. 50)(0. 97)/P(B) P(A/B)=0. 485

Ejemplo 1 : Probabilidades condicionales •

Ejemplo 1 : Probabilidades condicionales •

Ejemplo 1 : Probabilidades condicionales 4) Se escoge un producto al azar, y se nota que se encuentra en mal estado. ¿Cuál es la probabilidad de que es producto haya sido producido por la máquina B? Solución 1: Se separan los eventos condicionales de las hojas y se multiplican por sus ramificaciones considerando los espacios muestrales
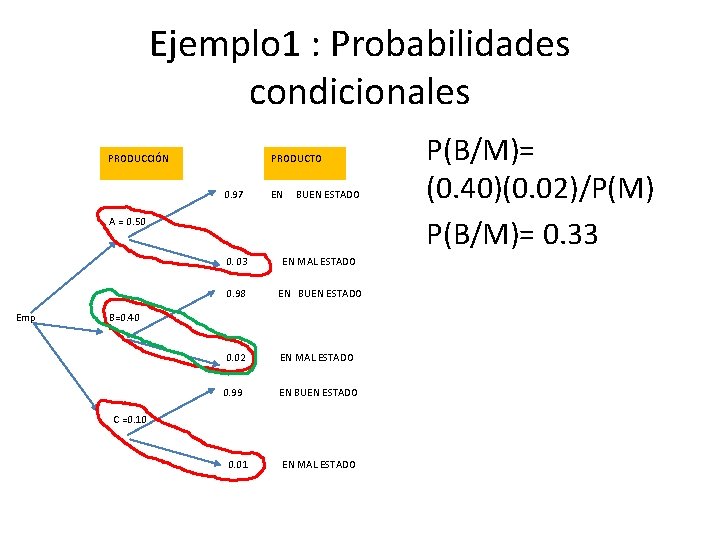
Ejemplo 1 : Probabilidades condicionales PRODUCCIÓN PRODUCTO 0. 97 EN BUEN ESTADO A = 0. 50 0. 03 EN MAL ESTADO 0. 98 EN BUEN ESTADO Emp B=0. 40 0. 02 EN MAL ESTADO 0. 99 EN BUEN ESTADO C =0. 10 0. 01 EN MAL ESTADO P(B/M)= (0. 40)(0. 02)/P(M) P(B/M)= 0. 33

Ejemplo 1 : Probabilidades condicionales •

Ejemplo 1 : Probabilidades condicionales •

Ejemplo 1 : Probabilidades condicionales 5) Se escoge un producto al azar, y se nota que se encuentra en buen estado. ¿Cuál es la probabilidad de que es producto haya sido producido por la máquina A? Solución 1: Se separan los eventos condicionales de las hojas y se multiplican por sus ramificaciones considerando los espacios muestrales
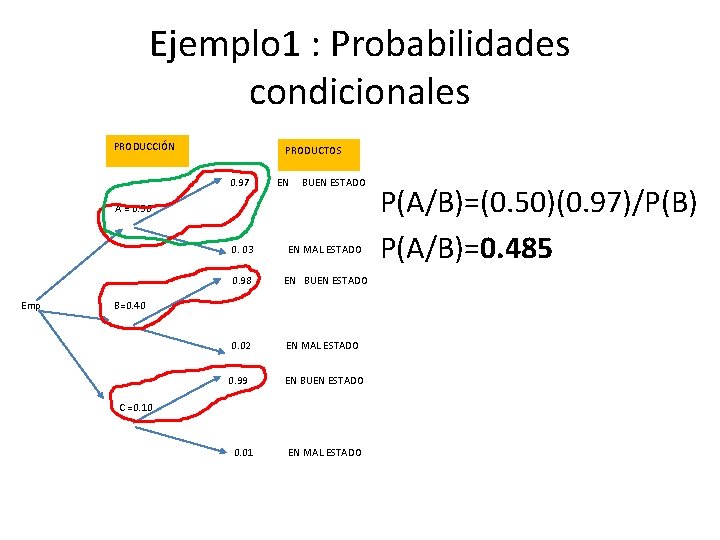
Ejemplo 1 : Probabilidades condicionales PRODUCCIÓN PRODUCTOS 0. 97 EN BUEN ESTADO A = 0. 50 0. 03 EN MAL ESTADO 0. 98 EN BUEN ESTADO Emp B=0. 40 0. 02 EN MAL ESTADO 0. 99 EN BUEN ESTADO C =0. 10 0. 01 EN MAL ESTADO P(A/B)=(0. 50)(0. 97)/P(B) P(A/B)=0. 485

Ejemplo 1 : Probabilidades condicionales 6) ¿Qué máquina produce con mayor eficiencia? PRODUCCIÓN PRODUCTOS 0. 97 EN BUEN ESTADO A = 0. 50 0. 03 EN MAL ESTADO 0. 98 EN BUEN ESTADO Emp B=0. 40 0. 02 EN MAL ESTADO 0. 99 EN BUEN ESTADO C =0. 10 0. 01 EN MAL ESTADO P(A/B)=(0. 50)(0. 97)/P(B) P(A/B)=0. 485 P(B/B)=(0. 40)(0. 98)/P(B) P(B/B)=0. 392 P(C/B)=(0. 10)(0. 99)/P(B) P(C/B)=0. 099

Ejemplo 1 : Probabilidades condicionales Una firma de consultoría renta automóviles de tres agencias, 20% de la agencia D, 20% de la agencia E y 60% de agencia F. Si 105 de los autos de D, 12% de los autos de E y 4% de los autos de F tienen neumáticos en mal estado, 1) ¿cuál es la probabilidad de que la firma tendrá un vehículo con neumáticos en mal estado?
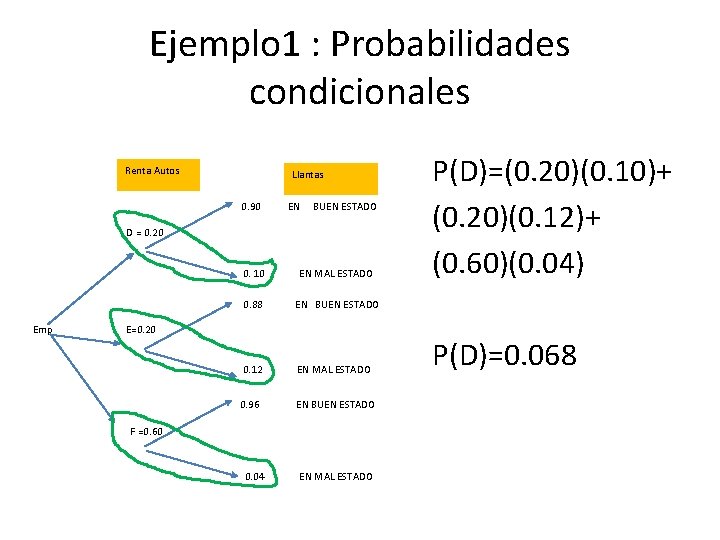
Ejemplo 1 : Probabilidades condicionales Renta Autos Llantas 0. 90 EN BUEN ESTADO D = 0. 20 0. 10 EN MAL ESTADO P(D)=(0. 20)(0. 10)+ (0. 20)(0. 12)+ (0. 60)(0. 04) 0. 88 EN BUEN ESTADO Emp E=0. 20 0. 12 EN MAL ESTADO 0. 96 EN BUEN ESTADO F =0. 60 0. 04 EN MAL ESTADO P(D)=0. 068

Ejemplo 2 : Probabilidades condicionales •

Ejemplo 2 : Probabilidades condicionales •

Ejemplo 2 : Probabilidades condicionales Si se alquila un vehículo con neumáticos en mal estado, ¿cuál es la probabilidad de que haya sido alquilado de E?
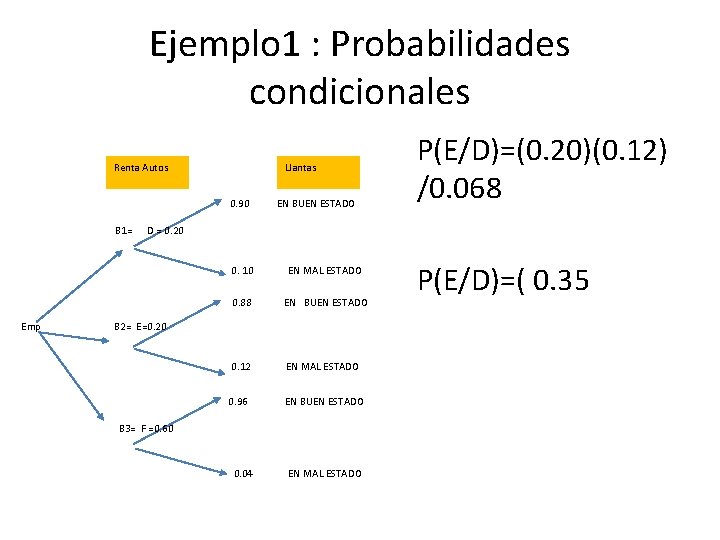
Ejemplo 1 : Probabilidades condicionales Renta Autos Llantas 0. 90 EN BUEN ESTADO P(E/D)=(0. 20)(0. 12) /0. 068 B 1= D = 0. 20 0. 10 EN MAL ESTADO 0. 88 EN BUEN ESTADO Emp B 2= E=0. 20 0. 12 EN MAL ESTADO 0. 96 EN BUEN ESTADO B 3= F =0. 60 0. 04 EN MAL ESTADO P(E/D)=( 0. 35

Ejemplo 1 : Probabilidades condicionales •
- Slides: 38