Privacy Enhancing Technologies ZeroKnowledge Proofs George Danezis g

Privacy Enhancing Technologies Zero-Knowledge Proofs George Danezis (g. danezis@ucl. ac. uk) With help from: Luca Melis (luca. melis. 14@ucl. ac. uk) Steve Dodier-Lazaro (s. dodier-lazaro. 12@ucl. ac. uk)

The GA 17 story so far … • Communications Confidentiality: • End-to-end encryption – protects content • Anonymous communications – protect meta-data • Computations Confidentiality: • SMPC: Homomorphic encryption & Secret sharing – protect private inputs and intermediate results of computations on private data. • Topic 4 & 5: Protect Integrity / authenticity & Privacy • Zero-knowledge proofs: protect integrity without revealing private data. • Credentials: protect authenticity without revealing private data. • Part 2 of GA 17: a bit less crypto; legal compliance; & various topics. • Labs 4 (& possibly 5) will be on ZK / Credentials.

A gentle introduction to Zero-Knowledge • Gentle definition: A zero-knowledge proof is • a protocol between a prover and a verifier; • that allows the prover to convince the verifier of a statement on secret(s); (integrity / soundness) • without revealing anything about the secret; (privacy / zero-knowledge) • A few caveats: • The properties may rely on the verifier being computationally bound (i. e. cannot break the Diffie-Hellman problem). • Some proof offer unconditional privacy! • Real-world equivalent: • I give you a sealed envelope, and wish to prove to you that I know the secret inside it, without revealing it. As a result of the protocol, you are convinced and have learned nothing about the secret in the envelope. • Is that even possible?

The Cave Analogy Locked door with keypad. • The prover wishes to convince a verifier that they have the code for opening the door. • A Zero Knowledge protocol: • The verifier stands by the entrance (and closes their eyes), while the prover choses at random to enter the cave left or right. • The verifier pick at random left or right and asks the prover to exit from this direction. • The prover comes out from the requested direction. • Three phases: Cave Entrance • Commit witness, Challenge, Respond. • Probability of cheating ½ • Repeat many times!

Why do we need Zero-Knowledge • This is the last time we talk about envelopes or caves. • Motivating example 1: • Signature schemes: “The signer needs to convince the verifier that they know the signature key (sk), and use it to sign a message, without revealing this secret key. All have the verification key (vk) and are convinced of the this statement”. • In practice: Signature key: sk = x in Zq Verification key: vk = gx where g is a public fixed generator of group G in which the DH problem is hard (eg. an appropriate EC group) • That sounds like a Zero-knowledge proof? (Convince you know the x such that vk = gx and public message)

Securing homomorphic encryption … • Motivating example 2: • Remember how homomorphic encryption works: (assume g, h public generators of G where the DH problem is hard) • Gen. Key(): priv = random x, pub=gx output (priv, pub) • Encrypt(m, pub): random k; output (gk, pubkhm) • Decrypt((a, b), priv): output (b·a-priv) • Two problems (from previous lecture): • How do you ensure the m is a valid vote? (m either 0 or 1)? • How to secure threshold decryption?

An attack on threshold decryption. • Threshold decryption in the honest-but-curious model: • Each authority runs the key generation and publish pubi (privi, pubi) = Gen. Key() • The global public key is: Global Pub = i pubi = g i xi • What is the last authority (say n) is actively malicious? • • • It does not follow the correct protocol steps. It derives privn, pubn = Gen. Key() It gives to the others: pubn’ = pubn / i/not n pubi Result: Global Pub = pubn = gprivn The corrupt authority n may decrypt all cipher texts on its own! • Solution: • Each authority publishes pubi and … • … a zero-knowledge proof they know a private priv such that pub = gpriv

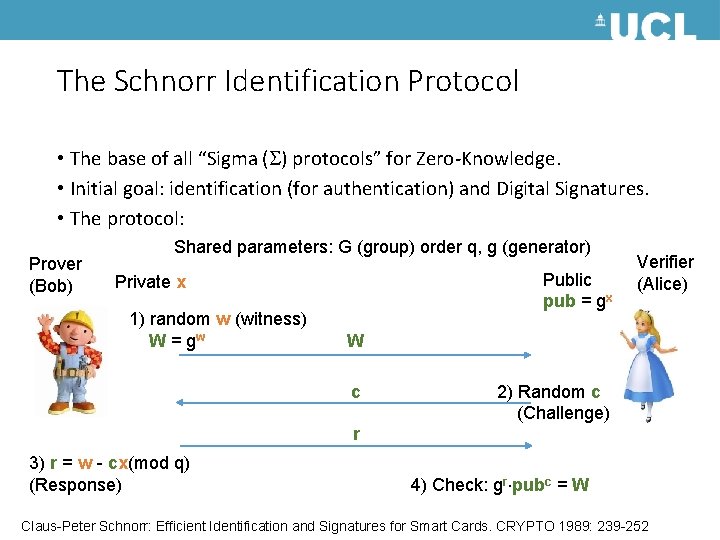
The Schnorr Identification Protocol • The base of all “Sigma ( ) protocols” for Zero-Knowledge. • Initial goal: identification (for authentication) and Digital Signatures. • The protocol: Prover (Bob) Shared parameters: G (group) order q, g (generator) Public pub = gx Private x 1) random w (witness) W = gw Verifier (Alice) W c 2) Random c (Challenge) r 3) r = w - cx(mod q) (Response) 4) Check: gr pubc = W Claus-Peter Schnorr: Efficient Identification and Signatures for Smart Cards. CRYPTO 1989: 239 -252

Key questions 1. Does the verification work? (soundness) 2. Does that prove Bob knows x? (Integrity / soundness) 3. Are we leaking any information about x? (privacy / zero-knowledge)

Does Schnorr verification work? • Check: gr pubc = W • Remember: r = w – cx (mod q) pub = gx W = gw • Do the algebra: • gr pubc = gw-cx gxc = gwgxc-xc = gw = W • OK that works! Note to help you remember: Focus on r = w – cx. Then raise g to the r.

Does Schnorr prove Bob knows x? • We prove this (sketch here) through a “rewinding argument”. • Insight into the argument: • Image there were only 2 challenges the verifier could chose from, c and c’. • However the prover cannot guess which is going to be used. • To be able to convince the verifier with prob > ½ it should be able to produce a correct answer for both c and c’ (given a fixed witness!). • i. e. if the prover chose c the prover should be able to produce: r = w – cx if the prover chose c’ the prover should be able to produce r’ = w – c’x Note: w stays same, everything after c, c’ changes. • Note: r = w – cx and r’ = w – c’x are 2 linear equations with two unknowns. • Therefore if the prover is able to convince the verifier with more than ½ probability they are able to extract the secret x – i. e. they know it.

Schnorr leaks no information about x? • We show this through a “simulation argument” (sketch here). • Insight: • ZK-proof is the transcript (W, c, r). • If anyone could make / forge such triplets, that pass the verification equation, then they cannot possibly leak any information about x! • Lets try: • Select a random r’’ • Select a random c’’ • Compute W’’ = gr’’ pubc’’ Note: We are not using the secret x! • The triplet (W’’, c’’, r’’) satisfies the verification equation, and is indistinguishable from the real protocol run. • So how comes the prover cannot cheat? • CAUSALITY: they need to commit to W before knowing c.

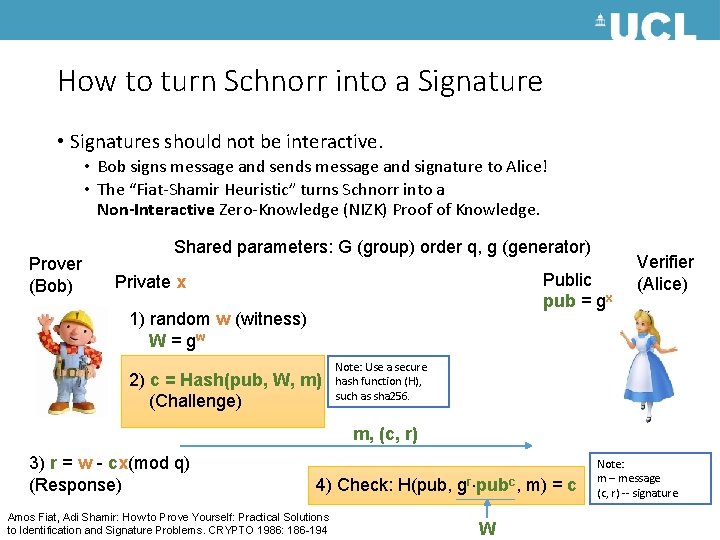
How to turn Schnorr into a Signature • Signatures should not be interactive. • Bob signs message and sends message and signature to Alice! • The “Fiat-Shamir Heuristic” turns Schnorr into a Non-Interactive Zero-Knowledge (NIZK) Proof of Knowledge. Prover (Bob) Shared parameters: G (group) order q, g (generator) Public pub = gx Private x 1) random w (witness) W = gw 2) c = Hash(pub, W, m) (Challenge) Verifier (Alice) Note: Use a secure hash function (H), such as sha 256. m, (c, r) 3) r = w - cx(mod q) (Response) 4) Check: H(pub, gr pubc, m) = c Amos Fiat, Adi Shamir: How to Prove Yourself: Practical Solutions to Identification and Signature Problems. CRYPTO 1986: 186 -194 W Note: m – message (c, r) -- signature

Why does the Fiat-Shamir Heuristic work? • Fiat-Shamir is a heuristic based on the security of the hash function H (say sha 256). • Cannot find pre-images (one-wayness / pre-image resistance) i. e. given Y = H(… y …), difficult to find a y what satisfies this equation. • Remember, to build a fake proof a simulator determines • first r’’ and c’’ • then W’’ • However, because c = H(…, W, …), the prover cannot first set c’’ and then W’’. • Insight: the use of the hash function forces causality. • Prover must first set W, and then c.

Summary of Schnorr • Identification Scheme: • Alice knows pub, and Bob may interactively prove he knows the private key x such that pub = gx. • Security arguments: • Soundness based on verification equation and extraction of the secret under rewinding. • Privacy based on the existence of a simulator algorithm that produces statistically indistinguishable proofs without knowledge of the secret. • Causality ensures proof is sound. • Signature scheme: • Same as Identification, but hash function used to derive challenge. • Hash function properties preserve causality. • No need to send the witness (W) to the verifier! • Know the Schnorr protocols! • They form the basis for very practical ZK proofs of more than knowledge!

Back to “why we care? ” … • Motivating example 1: Signatures • Hey, now we know how to build an efficient signature scheme based on the DL problem! • Motivating example 2 b: Proof of knowledge of the key pubi=gprivi • We can use a the Schnorr protocol (or NIZK) to prove this! • But: Can we do more than “Proofs of Knowledge”? • Examples from previous week (private computations) • The total of my votes is 1. • Each ciphertext is either 0 or 1. • More general: • The secret z = 3 x + 4 y – 10 • Or secret z = xy

We can prove “any” statement about encrypted / committed secrets! • Theory: • Is we can prove addition and multiplication … • E. g. for secrets x and y • The secret z = 3 x + 4 y – 10 • Or secret z = xy • … then we can prove all the inputs and the intermediate values the inputs and outputs of a network of NAND gates. • Therefore we can prove “any logic circuit” • Practice: • There are more efficient proofs for interesting statements.

Roadmap 1. 2. 3. 4. 5. First non-knowledge statement: equality! Pedersen Commitments. Proofs of discrete logarithm representations (extended Schnorr). Proofs of linear statements. Proofs of multiplication of secrets.

Proof of Equality of Discrete Logarithms • As ever g, h are generators of G or order q (in which DL is hard). • Consider P 1 = gx and P 2 = hx • Bob wants to prove the statement: NIZK{(x): P 1=gx and P 2=hx} • Protocol: Secrets Statement • Compose 2 Schnorr with the same witness / response. • Prover (Bob) computes: • • Random w; W 1 = gw; W 2 = hw Compute c = H(g, h, P 1, P 2, W 1, W 2) Compute r = w – cx Send (c, r) to Verifier (Alice) Note: keep w/r the same for values that are to be proved equal! Alice’s Verification: H(h, g, P 1, P 2, gr P 1 c, hr P 2 c) == c

Encryption vs. Commitments • Encryption / Decryption: • Allows Bob to encrypt a secret under the public key of Alice. • Running Example: Benaloh Additive homomorphic scheme. • Zero-knowledge proofs may prove some statements about the encrypted values! (e. g. they are 0/1, they add to 1, etc) • Commitments: • Insight: like an safe that can only be opened by the person with the key. • 2 operations: • C, o = Commit(v) • Reveal(C, v, o) • 2 properties: • Hiding: a commitment reveals nothing about the committed value. • Binding: one can only open the commitment and reveal the committed value (cannot pretend it was a commitment to another value. )

Chaum-Pedersen Commitments • Shared parameters: • A group G with order q (with hard DL) • A generator g and h of G. • Define the terms: • v – value to be committed; • Commit(v): • Random o in Zq • C = g v ho • Output (C, o) • Reveal(C, v, o): • Return gvho == C • C – the commitment; • o – a random nonce (in Zq) called “the opening” (kept secret until “reveal”) Instead of proving statements about encrypted values, we can prove statements about committed values without revealing them.

Proof of Knowledge of DL representations How can we prove we know the value committed within a Pedersen Commitment (without revealing it)? • Reminder: Commitment representation C = gvho Variant of Schnorr (due to Brands / Camenisch): • Prover (Bob) produces: Note: Witness W has the same “shape” random w 1, w 2; W = gw 1 hw 2 as Commitment. c = H(g, h, C, W) r 1 = w 1 – c v r 2 = w 2 – c o Send (c, r 1, r 2) • Verifier (Alice) checks: Why? : gr 1 hr 2 Cc H(g, h, C, gr 1 hr 2 Cc) == c = gw 1 -cvhw 2 -co. Cc =(gw 1 hw 2)(gvho)-c. Cc = W C-c. Cc =W See Chapter 3 of Stefan Brands “Rethinking Public Key Infrastructures and Digital Certificates; Building in Privacy” (available online)

DL representations proofs in general • Assuming: • Prover (Bob): random … wi …; W = i giw c = H(… gi …, C, W) ri = w i – c v Send (c, … ri …) • gi generators of G • xi secrets • C = i gixi • We can prove the statement: NIZK{(xi): C = i g i xi } • Important: • If you can reduce a ZK proof to a DL representation proof, you have a recipe to prove it! • Remember: equality can be proven by simply using the same w/r for equal values. i • Verifier (Alice) checks: H(… gi …, C, ( i giri)Cc) == c? Exercise: ensures this check succeeds.

Proof of linear relations • Consider 3 commitments on secrets x, y and z = a x + b y + d (mod q): • Cx = gxho 1 • Cy = gyho 2 • Cz = gzho 3 • How can we prove in Zero-Knowledge this statement? • NIZK{(x, y, z, oi): Cx = gxho 1 and Cy = gyho 2 and Cz = gzho 3 and z = a x + b y + d } • Solution: substitute the linear relationship for z: • Cz = gzho 3 = g(a x + b y + d)ho 3 (Cz g-d) = (ga)x (gb)y ho 3 • Thus it is sufficient to prove: NIZK{(x, y, z, oi): Cx = gxho 1 and Cy = gyho 2 and (Cz g-d) = (ga)x (gb)y ho 3} Using DL representation & equality proofs. Note: there will be no w/r for the dependent z value!

Exercise on proving linear relations • Given the commitment on secrets x, y, z, o: C = g 1 x g 2 y g 3 z g 4 o • 1) What is the procedure to prove and verify non-interactively the statement: NIZK{(x, y, z, o): C = g 1 x g 2 y g 3 z g 4 o and z = 10 x - 5 y - 1} • 2) What is the procedure to prove and verify non-interactively the statement: NIZK{(x, y, z, o): C = g 1 x g 2 y g 3 z g 4 o and x=y and z=10}

Proof of products of secret values • Assume we have commitments on secrets x, y, z, oi: • Cx = gxho 1 • Cy = gyho 2 • Cz = gzho 3 • We wish to prove the statement: NIZK{(x, y, z, oi): Cx = gxho 1 and Cy = gyho 2 and Cz = gzho 3 and z = x y (mod q)} • A naïve protocol: Define D = Cxy hs ( = gxy h(o 1 y+s) ) Prove NIZK{(x, y, z, oi, s, o’’): Cx = gxho 1 and Cy = gyho 2 and Cz = gzho 3 and D=Cxy hs and D=gzho’’} • Inefficient, but it works!

Exercises • The prover has just: • • encrypted a ciphertext of m with random number r under public key pub as Encpub(m; r) (A = gr, B = pubr hm) • Construct the proof / verification procedures for the following statements: 1. NIZK{(r, m): A = gr and B = pubr hm} (Proof of knowledge of the plaintext, i. e. Enc(m; r) = (A, B) ). 2. NIZK{(r, m): A = gr and B = pubr hm and m(1 -m) = 0} (Proof that m is either 0 or 1)

Exercise: Securing the Polling example • The prover has encrypted 2 ciphertexts of m 1 and m 2 under pub • Enc(m 1; r 1) = (A 1, B 1) and Enc(m 2; r 2) =(A 2, B 2). • Which set of DL representation proofs would allow you to prove the following statement? • NIZK{(m 1, m 2, r 1, r 2): Enc(m 1; r 1) = (A 1, B 1) and Enc(m 2; r 2) =(A 2, B 2) and (m 1 = 0 or m 1 = 1) and (m 2 = 0 or m 2 = 1) and m 1 + m 2 = 1} Note: use the proofs from the previous exercises to prove correct encryption, as well as m(1 -m) =0.

Conclusions • Zero-knowledge • a key building block to achieve privacy and integrity. • Interactive: proofs of extraction (integrity) and simulation (privacy) are key! • Non-interactive: can be used to build signatures / Heuristic. • Schnorr protocols compose well • • • Knowledge Equality DL representations Linear relations Multiplication … • Since we can prove linear relations and multiplicative relations between secrets, we can prove the correctness of any hidden digital circuit (NAND). • More efficient protocols are usually available.