Priority Search Trees Modified Prof Sahnis notes Priority

Priority Search Trees • Modified Prof. Sahni’s notes

Priority Search Trees • Keys are distinct ordered pairs (xi, yi). • Basic operations. § get(x, y) … return element whose key is (x, y). § delete(x, y) … delete and return element whose key is (x, y). § insert(x, y, e) … insert element e, whose key is (x, y). • Rectangle operations.

min. Xin. Rectangle(x. L, x. R, y. T) • Return element with min x-coordinate in the rectangle defined by the lines, x= x. L, x= x. R, y = 0, y = y. T, x. L <= x. R, 0 <= y. T x. L x. R • I. e. , return element with min x such that x. L <= x. R and 0 <= y. T.

max. Xin. Rectangle(x. L, x. R, y. T) • Return element with max x-coordinate in the rectangle defined by the lines, x= x. L, x= x. R, y = 0, y = y. T, x. L <= x. R, 0 <= y. T x. L x. R • I. e. , return element with max x such that x. L <= x. R and 0 <= y. T.

min. Yin. Xrange(x. L, x. R) • Return element with min y-coordinate in the rectangle defined by the lines, x= x. L, x= x. R, y = 0, y = infinity, x. L <= x. R. x. L x. R • I. e. , return element with min y such that x. L <= x. R.

enumerate. Rectangle(x. L, x. R, y. T) • Return all elements in the rectangle defined by the lines, x= x. L, x= x. R, y = 0, y = y. T, x. L <= x. R, 0 <= y. T x. L x. R • I. e. , return all elements such that x. L <= x. R and 0 <= y. T.

Complexity • O(log n) for each operation except for enumerate. Rectangle, where n is the number of elements in the tree. • Complexity of enumerate. Rectangle is O(log n + s), where s is the number of elements in the rectangle.

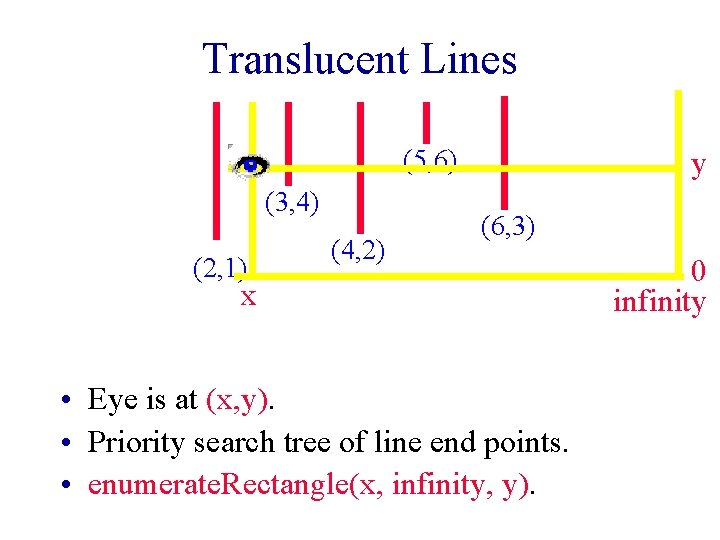
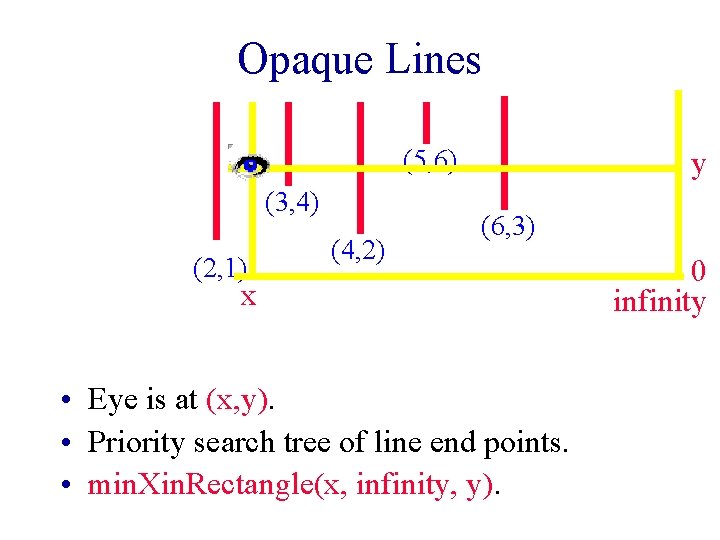
Applications – Visibility • Dynamic set of semi-infinite vertical line segments. § Vertical lines with end points (xi, infinity) and (xi, yi). (5, 6) (3, 4) (2, 1) (4, 2) (6, 3) Opaque/translucent lines.

Translucent Lines (5, 6) (3, 4) (2, 1) (4, 2) y (6, 3) x • Eye is at (x, y). • Priority search tree of line end points. • enumerate. Rectangle(x, infinity, y). 0 infinity

Opaque Lines (5, 6) (3, 4) (2, 1) (4, 2) y (6, 3) x • Eye is at (x, y). • Priority search tree of line end points. • min. Xin. Rectangle(x, infinity, y). 0 infinity

Online Intersection Of Linear Intervals • Intervals are of the form [i, j], i < j. • [i, j] may, for example represent the fact that a machine is busy from time i to time j. • Answer queries of the form: which intervals intersect/overlap with a given interval [u, v], u < v. § List all machines that are busy at any time between u and v.

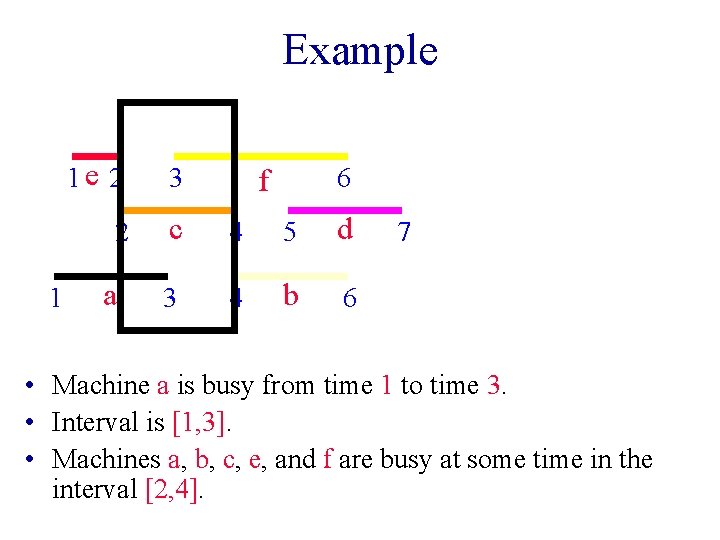
Example 1 1 e 2 3 2 c 4 5 d 3 4 b 6 a 6 f 7 • Machine a is busy from time 1 to time 3. • Interval is [1, 3]. • Machines a, b, c, e, and f are busy at some time in the interval [2, 4].

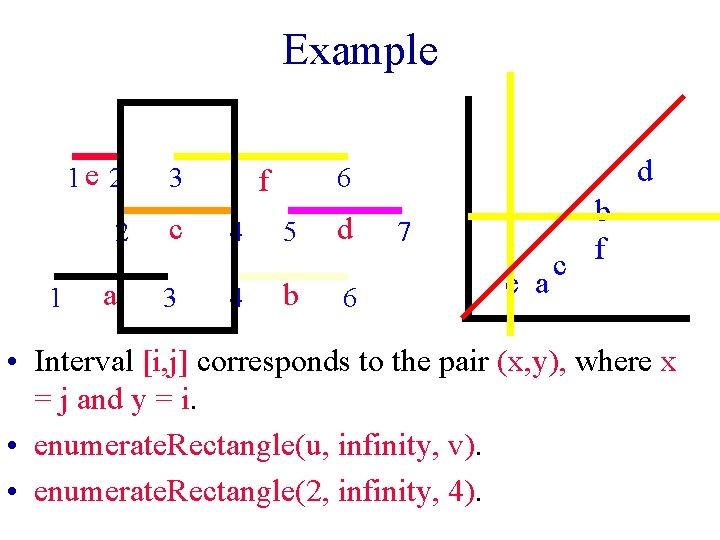
Example 1 1 e 2 3 2 c 4 5 d 3 4 b 6 a d 6 f 7 e a b f c • Interval [i, j] corresponds to the pair (x, y), where x = j and y = i. • enumerate. Rectangle(u, infinity, v). • enumerate. Rectangle(2, infinity, 4).

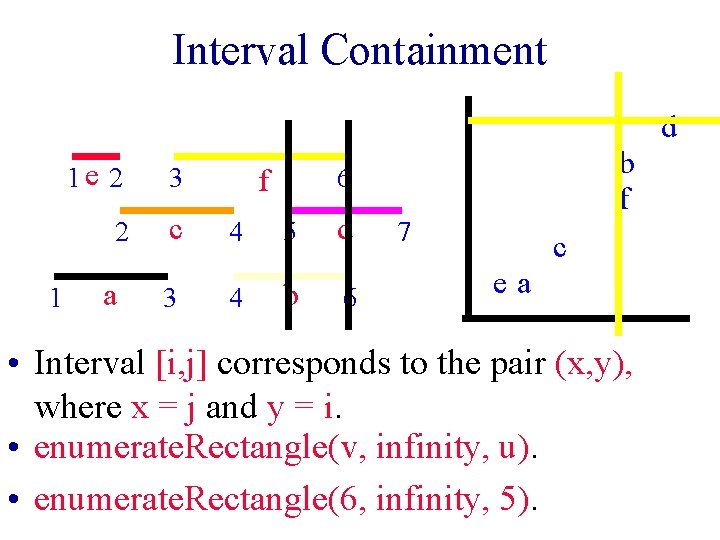
Interval Containment • List all intervals [i, j] that contain the interval [u, v]. § [i, j] contains [u, v] iff i <= u <= v <= j. 1 1 e 2 3 2 c 4 5 d 3 4 b 6 a 6 f 7 [u, v] = [5, 6]

Interval Containment d 1 1 e 2 3 2 c 4 5 d 3 4 b 6 a b f 6 f 7 c ea • Interval [i, j] corresponds to the pair (x, y), where x = j and y = i. • enumerate. Rectangle(v, infinity, u). • enumerate. Rectangle(6, infinity, 5).

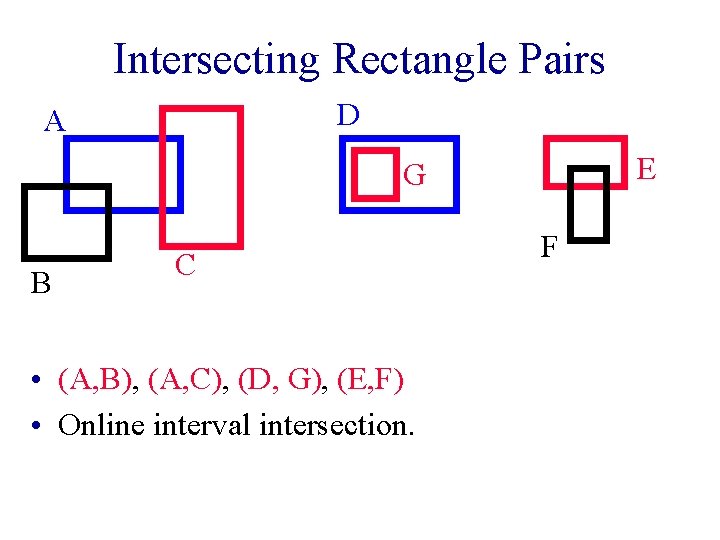
Intersecting Rectangle Pairs D A E G B C • (A, B), (A, C), (D, G), (E, F) • Online interval intersection. F

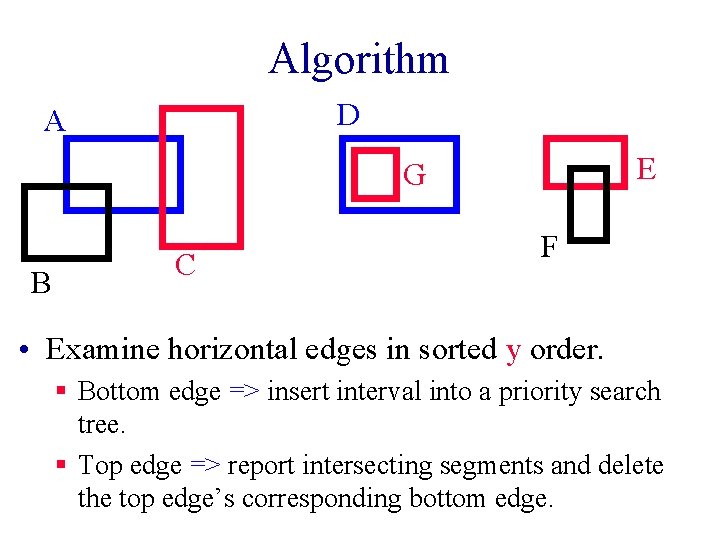
Algorithm D A E G B C F • Examine horizontal edges in sorted y order. § Bottom edge => insert interval into a priority search tree. § Top edge => report intersecting segments and delete the top edge’s corresponding bottom edge.

Complexity • Examine edges in sorted order. § Bottom edge => insert interval into a priority search tree. § Top edge => report intersecting segments and delete the top edge’s corresponding bottom edge. • O(n log n) to sort edges by y, where n is # of rectangles. § Insert n intervals … O(n log n). § Report intersecting segments … O(n log n + s). § Delete n intervals … O(n log n).

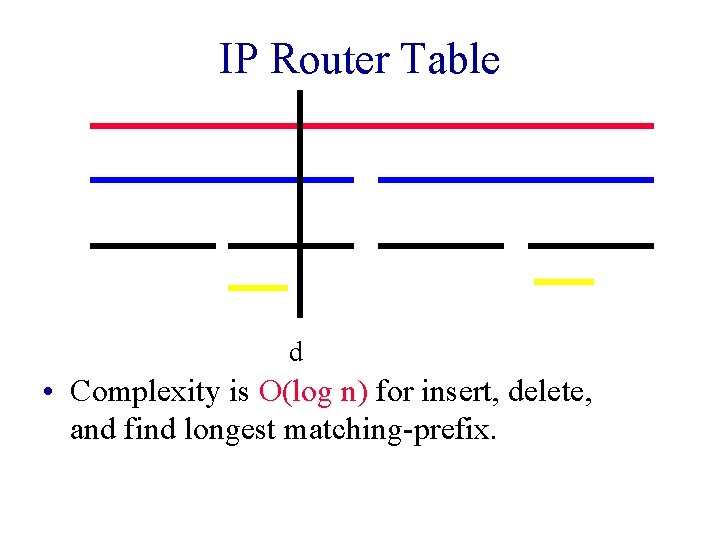
IP Router Table • Longest-prefix matching § 10*, 101*, 1001* § Destination address d = 10100 § Longest matching-prefix is 101* • Prefix is an interval § d is 5 bits => 101* = [10100, 10111] = [20, 23] • 2 prefixes may nest but may not have a proper intersection

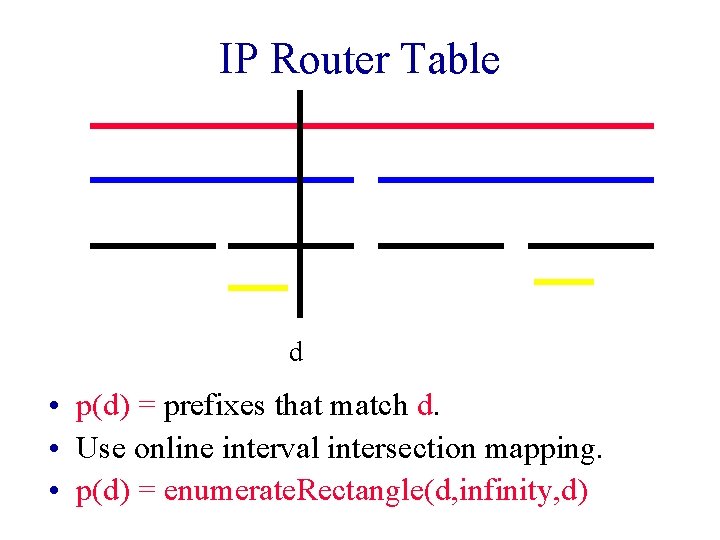
IP Router Table d • p(d) = prefixes that match d. • Use online interval intersection mapping. • p(d) = enumerate. Rectangle(d, infinity, d)

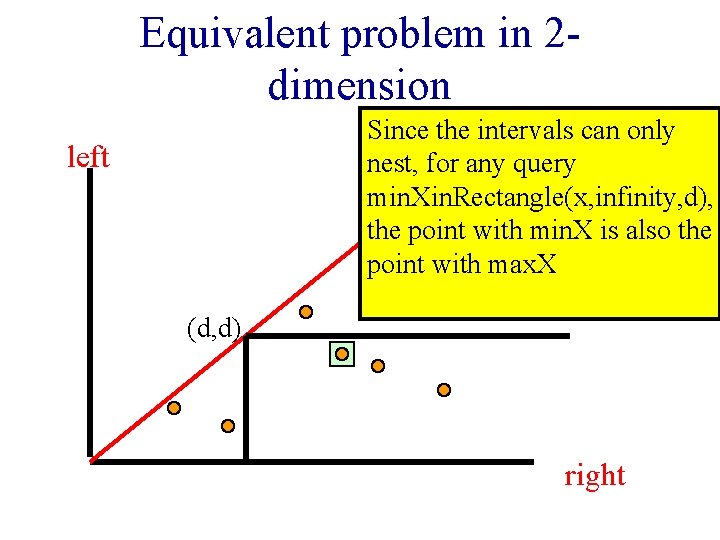
Equivalent problem in 2 dimension Since the intervals can only nest, for any query min. Xin. Rectangle(x, infinity, d), the point with min. X is also the point with max. X left (d, d) right

IP Router Table d • Complexity is O(log n) for insert, delete, and find longest matching-prefix.