Priority Queues Heaps Sections 6 1 to 6





![Heap example § § § Parent of v[k] = v[k/2] Left child of v[k] Heap example § § § Parent of v[k] = v[k/2] Left child of v[k]](https://slidetodoc.com/presentation_image_h2/a661da41da0040cc9697d684228eadb1/image-8.jpg)












- Slides: 26

Priority Queues (Heaps) § Sections 6. 1 to 6. 5 1

The Priority Queue ADT § Delete. Min – log N time § Insert – log N time § Other operations – Find. Min § Constant time – Initialize § N time 2

Applications of Priority Queues § Any event/job management that assign priority to events/jobs § In Operating Systems – Scheduling jobs § In Simulators – Scheduling the next event (smallest event time) 3

Priority Queue Implementation § Implemented as adaptor class around – Linked lists § O(N) worst-case time on either insert() or delete. Min() – Binary Search Trees § O(log(N)) average time on insert() and delete() § Overkill: all elements are sorted – However, we only need the minimum element – Heaps § This is what we’ll study and use to implement Priority Queues § O(log. N) worst case for both insertion and delete operations 4

Partially Ordered Trees § A partially ordered tree (POT) is a tree T such that: – There is an order relation <= defined for the vertices of T – For any vertex p and any child c of p, p <= c § Consequences: – The smallest element in a POT is the root – No conclusion can be drawn about the order of children 5

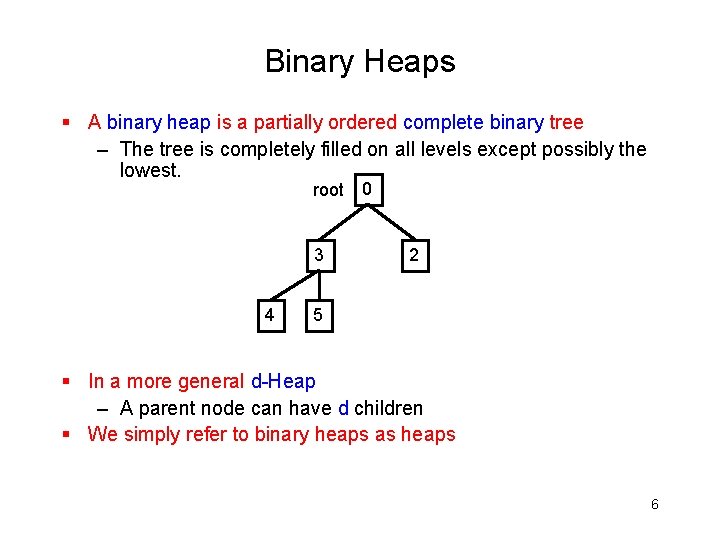
Binary Heaps § A binary heap is a partially ordered complete binary tree – The tree is completely filled on all levels except possibly the lowest. root 3 4 0 2 5 § In a more general d-Heap – A parent node can have d children § We simply refer to binary heaps as heaps 6

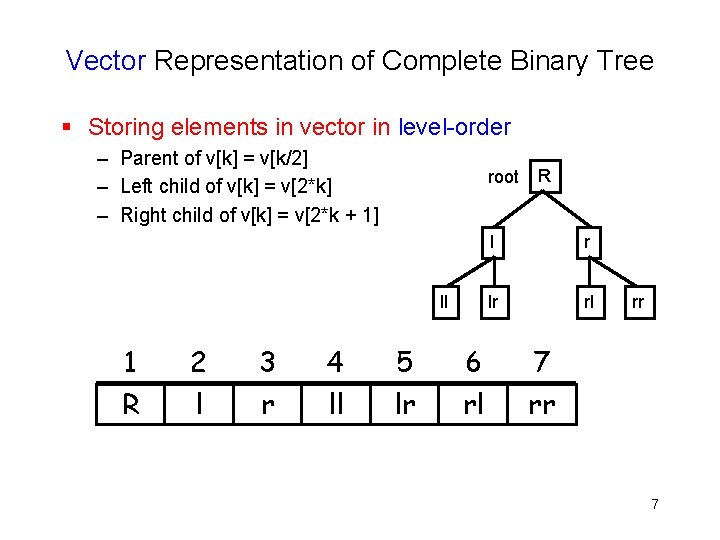
Vector Representation of Complete Binary Tree § Storing elements in vector in level-order – Parent of v[k] = v[k/2] – Left child of v[k] = v[2*k] – Right child of v[k] = v[2*k + 1] root ll 1 R 2 l 3 r 4 ll 5 lr 6 rl R l r lr rl rr 7
![Heap example Parent of vk vk2 Left child of vk Heap example § § § Parent of v[k] = v[k/2] Left child of v[k]](https://slidetodoc.com/presentation_image_h2/a661da41da0040cc9697d684228eadb1/image-8.jpg)
Heap example § § § Parent of v[k] = v[k/2] Left child of v[k] = v[2*k] Right child of v[k] = v[2*k + 1] 8

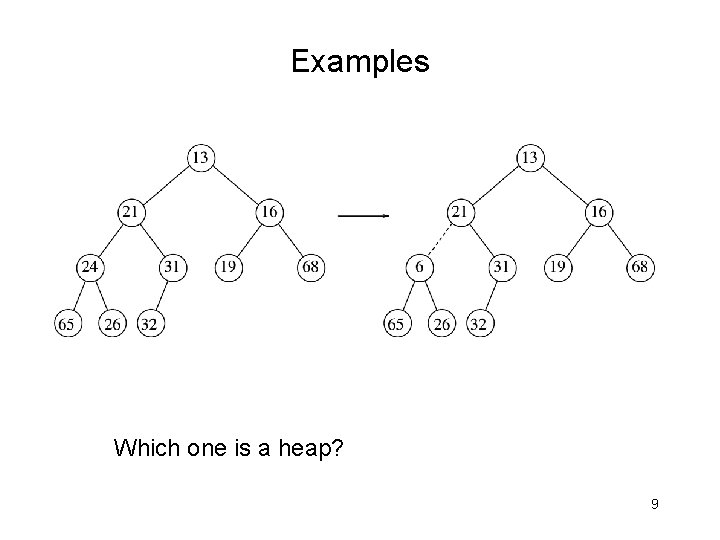
Examples Which one is a heap? 9

Implementation of Priority Queue (heap) 10

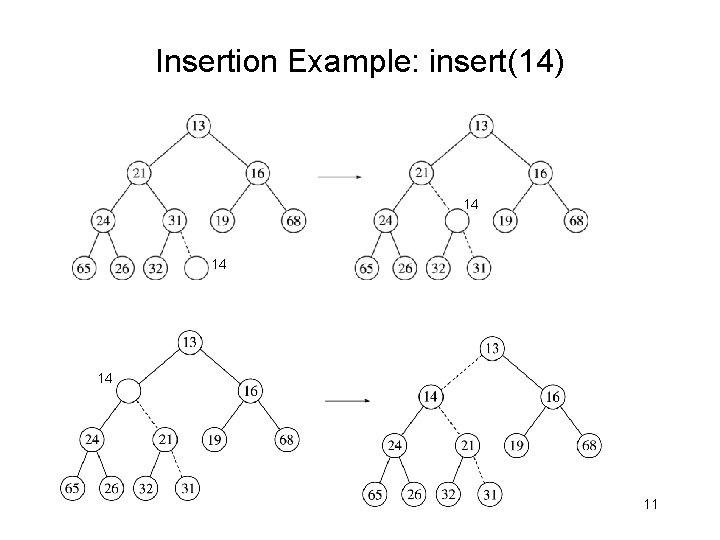
Insertion Example: insert(14) 14 14 14 11

Basic Heap Operations: insert(x) § Maintain the complete binary tree property and fix any problem with the partially ordered tree property – Create a leaf at the end – Repeat § Locate parent § if POT not satisfied – Swap with parent § else – Stop – Insert x into its final location 12

Implementation of insert 13

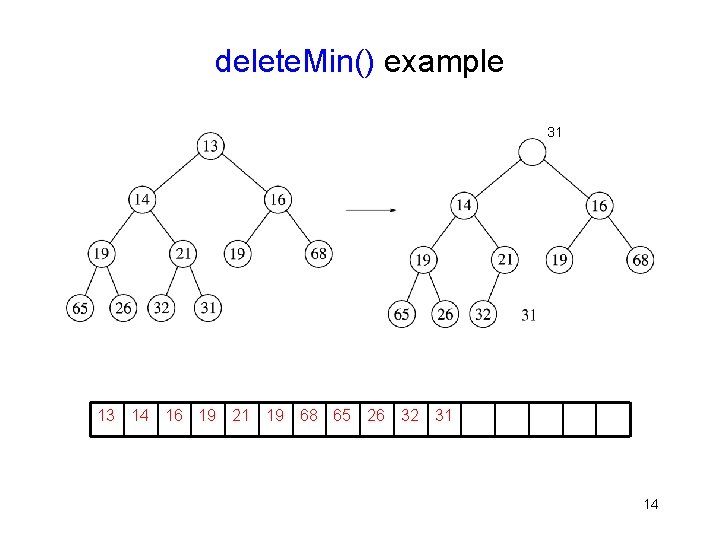
delete. Min() example 31 13 14 16 19 21 19 68 65 26 32 31 14

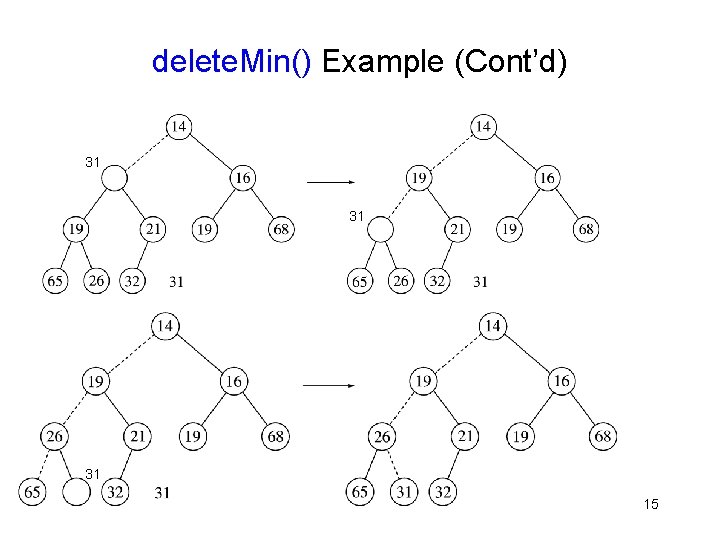
delete. Min() Example (Cont’d) 31 31 31 15

Basic Heap Operations: delete. Min() § Replace root with the last leaf ( last element in the array representation – This maintains the complete binary tree property but may violate the partially ordered tree property § Repeat – Find the smaller child of the “hole” – If POT not satisfied § Swap hole and smaller child – else § Stop 16

Implementation of delete. Min() 17

Implementation of delete. Min() 18

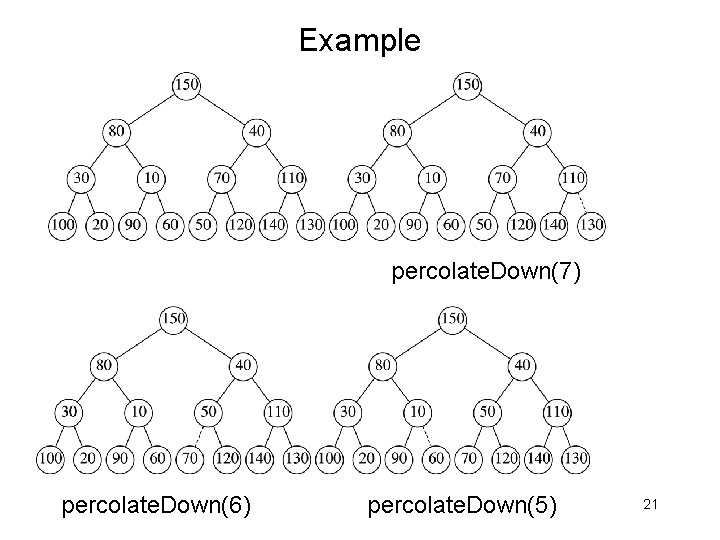
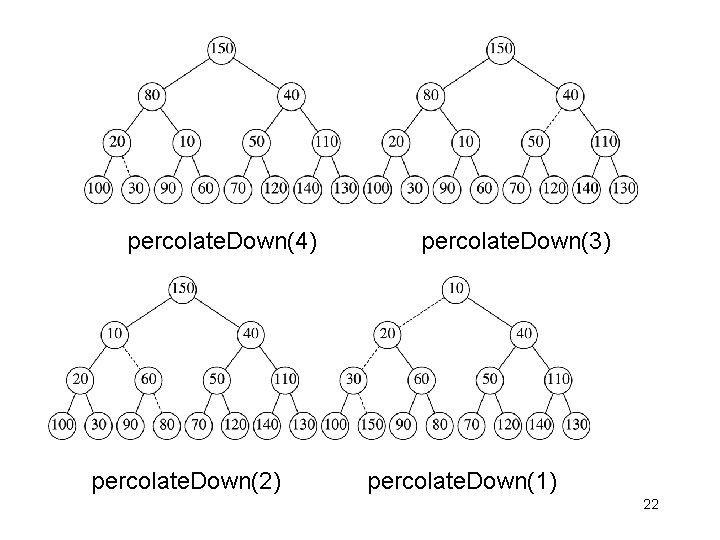
Constructor § Construct heap from a collection of item § How to? – – Naïve methods Insert() each element Worst-case time: O(N(log. N)) We show an approach taking O(N) worst-case § Basic idea – First insert all elements into the tree without worrying about POT – Then, adjust the tree to satisfy POT, starting from the bottom 19

Constructor 20

Example percolate. Down(7) percolate. Down(6) percolate. Down(5) 21

percolate. Down(4) percolate. Down(2) percolate. Down(3) percolate. Down(1) 22

Complexity Analysis § Consider a tree of height h with 2 h-1 nodes – Time = 1 • (h) + 2 • (h-1) + 4 • (h-2) +. . . + 2 h-1 • 1 – = i=1 h 2 h-i i = 2 h i=1 h i/2 i – = 2 h O(1) = O(2 h) = O(N) § Proof for i=1 h i/2 i = O(1) – i/2 i ≤ ∫i-1 i (x+1)/2 x dx – i=1 h i/2 i ≤ i=1∞ i/2 i ≤ ∫ 0∞ (x+1)/2 x dx § Note: ∫u dv = uv - ∫v du, with dv = 2 x and u = x and ∫ 2 -x dx = 2 -x/ln 2 – ∫ 0∞ (x+1)/2 x dx = -x 2 -x/ln 2|0∞ + 1/ln 2 ∫ 0∞ 2 -x dx + ∫ 0∞ 2 -x dx – = -2 -x/ln 2 2|0∞ - 2 -x/ln 2|0∞ = (1 + 1/ln 2)/ln 2 = O(1) 23

Alternate Proof § Prove i=1 h i/2 i = O(1) – – – i=0∞ xi = 1/(1 -x) when |x| < 1 Differentiating both sides with respect to x we get i=0∞ i xi-1 = 1/(1 -x)2 So, i=0∞ i xi = x/(1 -x)2 Substituting x = 1/2 above gives i=0∞ i 2 -i = 0. 5/(1 -0. 5)2 = O(1) 24

C++ STL Priority Queues § priority_queue class template – Implements delete. Max instead of delete. Min in default – Max. Heap instead of Min. Heap § Template – Item type – container type (default vector) – comparator (default less) § Associative queue operations – Void push(t) – void pop() – T& top() – void clear() – bool empty() 25

26