Priority Queues Heaps CS 202 Fundamental Structures of

Priority Queues (Heaps) CS 202 – Fundamental Structures of Computer Science II Bilkent University Computer Engineering Department CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 1

Need for priority based retrievel n Some applications require different treatments for items n Printer queue q n OS scheduler q n Items (files to be printed) can be prioritized depending on their size. It may be better to schedule smaller sized programs before larger sized programs. Priority queue structure can be used to model these kind of applications n So that some operations (like finding the highest priority item) can be implemented very efficiently. CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 2

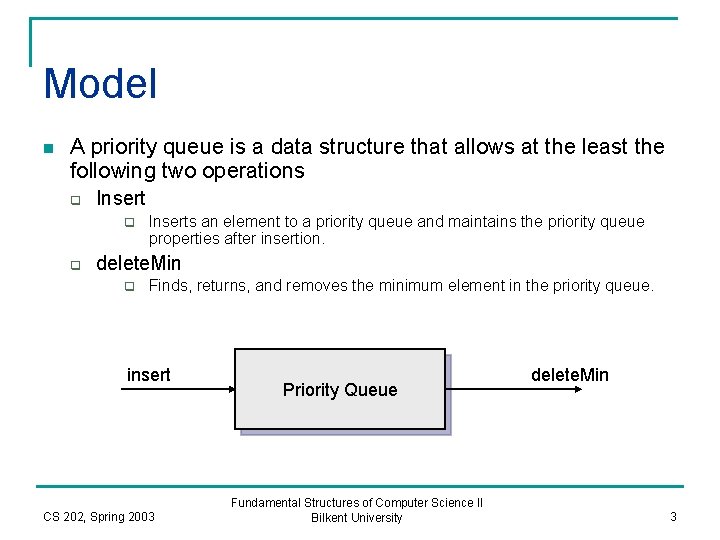
Model n A priority queue is a data structure that allows at the least the following two operations q Insert q q Inserts an element to a priority queue and maintains the priority queue properties after insertion. delete. Min q Finds, returns, and removes the minimum element in the priority queue. insert CS 202, Spring 2003 Priority Queue Fundamental Structures of Computer Science II Bilkent University delete. Min 3

Simple Implementations of priority queues n Use a simple linked list q q n Insert to the head of the list (O(1)) Search for an item by traversing the list from start to end or until item found (O(N)). Use a binary search tree q q Insert into the tree. (O(log. N)) Remove from the tree (O(log. N)). CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 4

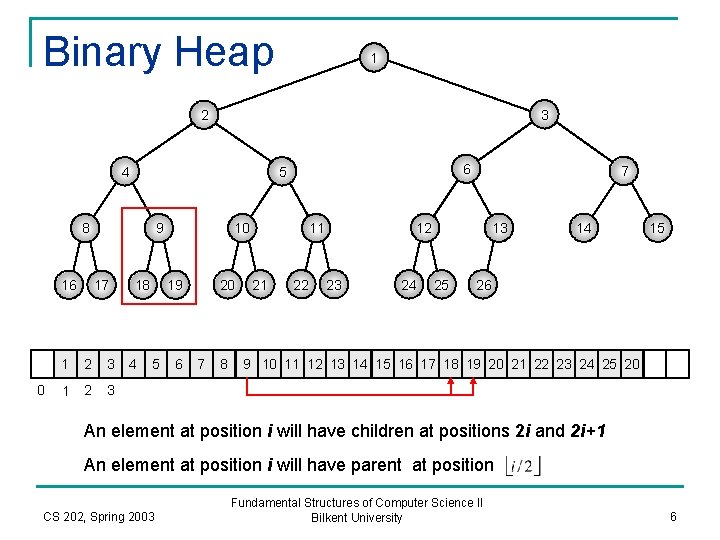
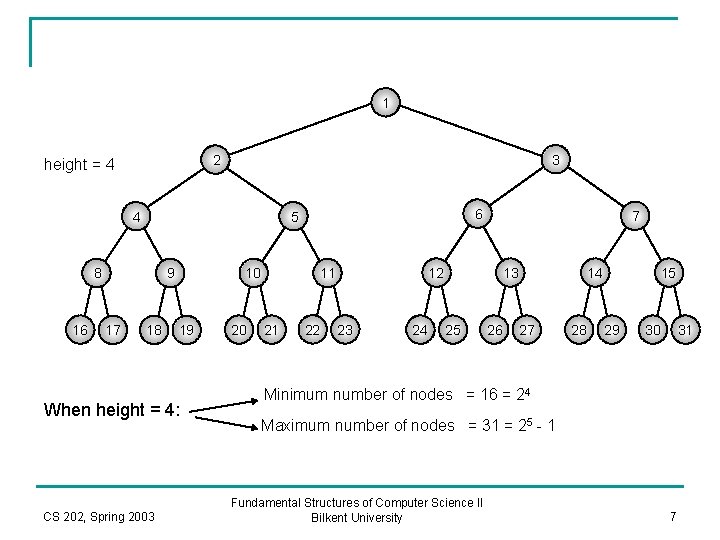
Binary Heap (or Heap) n It is a complete binary tree. q n n A tree that is completely filled except the bottom level, which is strictly filled from left to right. A complete binary tree of height h has between 2 h and 2 h+1 – 1 nodes. The height of a complete binary tree is: CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 5

Binary Heap 1 3 2 4 8 16 0 9 17 1 2 3 6 5 18 4 10 20 19 5 6 7 8 12 11 21 22 7 23 24 13 25 14 15 26 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 20 An element at position i will have children at positions 2 i and 2 i+1 An element at position i will have parent at position CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 6

1 3 2 height = 4 4 8 16 9 17 6 5 18 10 19 When height = 4: CS 202, Spring 2003 20 12 11 21 22 7 23 24 13 25 26 14 27 28 15 29 30 31 Minimum number of nodes = 16 = 24 Maximum number of nodes = 31 = 25 - 1 Fundamental Structures of Computer Science II Bilkent University 7

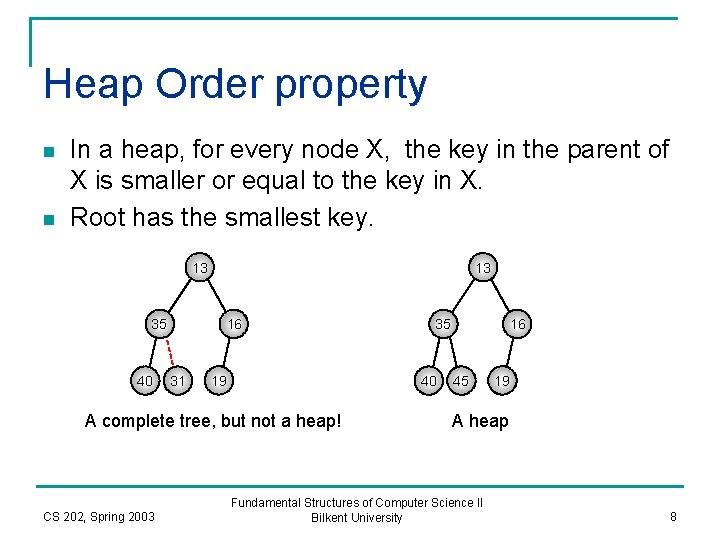
Heap Order property n n In a heap, for every node X, the key in the parent of X is smaller or equal to the key in X. Root has the smallest key. 13 13 35 40 16 31 19 40 A complete tree, but not a heap! CS 202, Spring 2003 35 16 45 19 A heap Fundamental Structures of Computer Science II Bilkent University 8

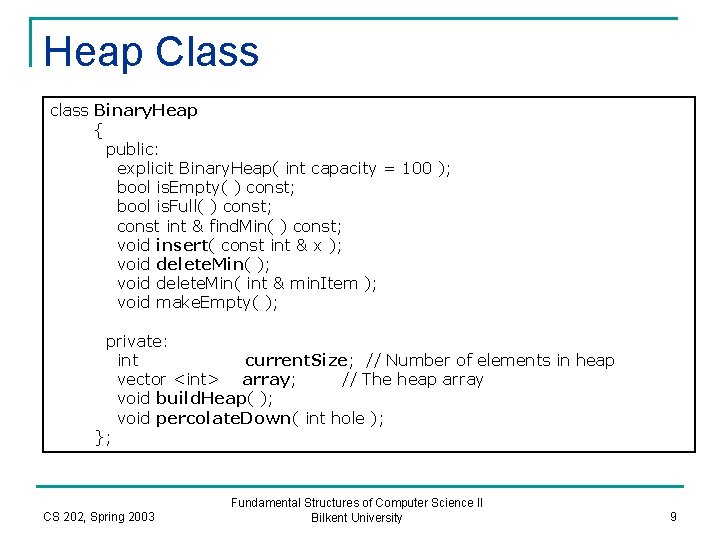
Heap Class class Binary. Heap { public: explicit Binary. Heap( int capacity = 100 ); bool is. Empty( ) const; bool is. Full( ) const; const int & find. Min( ) const; void insert( const int & x ); void delete. Min( int & min. Item ); void make. Empty( ); private: int current. Size; // Number of elements in heap vector <int> array; // The heap array void build. Heap( ); void percolate. Down( int hole ); }; CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 9

Heap Insert void Binary. Heap: : insert( const int & x ) { if( is. Full( ) ) throw Overflow( ); } // Percolate up int hole = ++current. Size; for( ; hole > 1 && x < array[ hole / 2 ]; hole /= 2 ) array[ hole ] = array[ hole / 2 ]; array[ hole ] = x; CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 10

Heap Delete Minimum void Binary. Heap: : delete. Min( ) { if( is. Empty( ) ) throw Underflow( ); } array[ 1 ] = array[ current. Size-- ]; percolate. Down( 1 ); CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 11

Heap Delete Minimum void Binary. Heap: : percolate. Down( int hole ) { int child; int tmp = array[ hole ]; } for( ; hole * 2 <= current. Size; hole = child ) { child = hole * 2; if( child != current. Size && array[ child + 1 ] < array[ child ]) child++; if( array[ child ] < tmp ) array[ hole ] = array[ child ]; else break; } array[ hole ] = tmp; CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 12

Other Heap Operations n Heap provides fast access to minimum element n n n But heap does not store any other ordering information. Searching for an arbitrary item is not easy q n O(long. N) worst case Requires O(N)) time. An other data structure needs to be kept if we want to do other operations also. CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 13

Other Heap Operations n If we assume that the position of other elements (other than minimum) is also known by some other methods, several operations become cheap q decrease. Key (p. D) q q increse. Key (p, D) q q Increases the value of the item at position p by D amount § Requires perculate down remove (p) q q Lowers the value of the item at position p by D amount. § Requires percolate up Removes the item at position p § decrease. Key(p, ∞) and delete. Min(); Build. Heap q Take N items and place them into an empty heap. CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 14

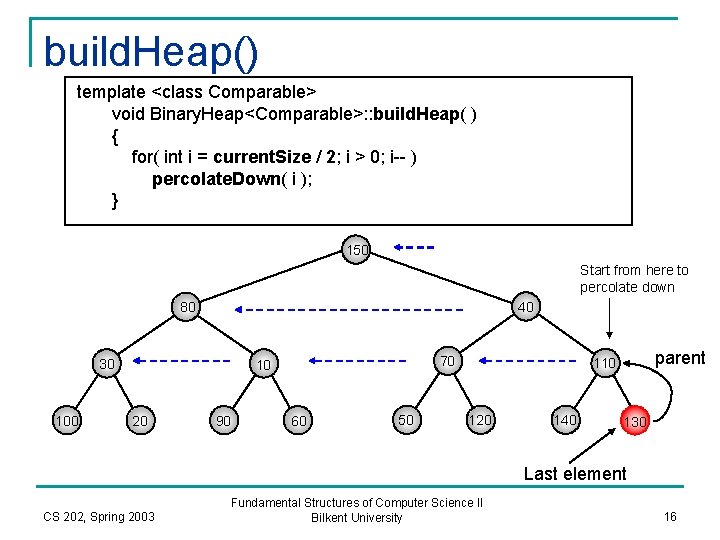
build. Heap() n Takes N items and builds a heap. q n A more efficient method exists. q n Simple method is: Insert N items successively. O(N) running time. Sketch of Algorithm q q 1. Position = lowerbound(heap. Siz/2); // initial position 2. perculate. Down item at that position. 3. Decrement position by one. 4. Repeat steps 2, 3, 4 until position is 0. CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 15

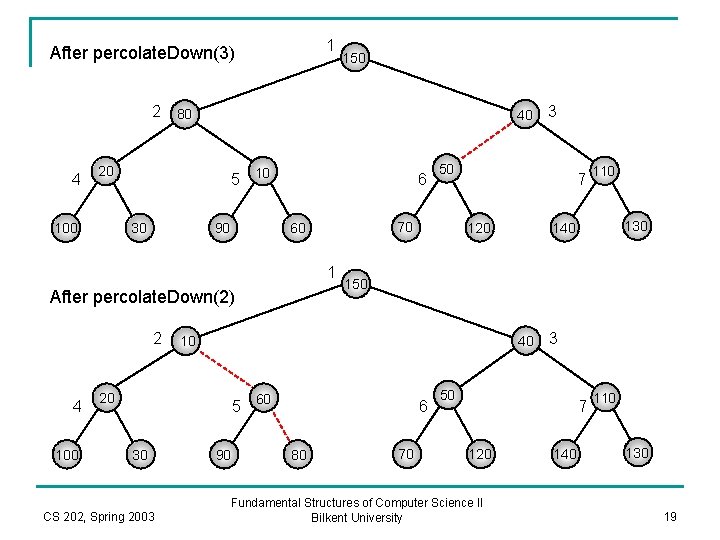
build. Heap() template <class Comparable> void Binary. Heap<Comparable>: : build. Heap( ) { for( int i = current. Size / 2; i > 0; i-- ) percolate. Down( i ); } 150 Start from here to percolate down 80 40 30 100 70 10 20 90 60 50 parent 110 120 140 130 Last element CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 16

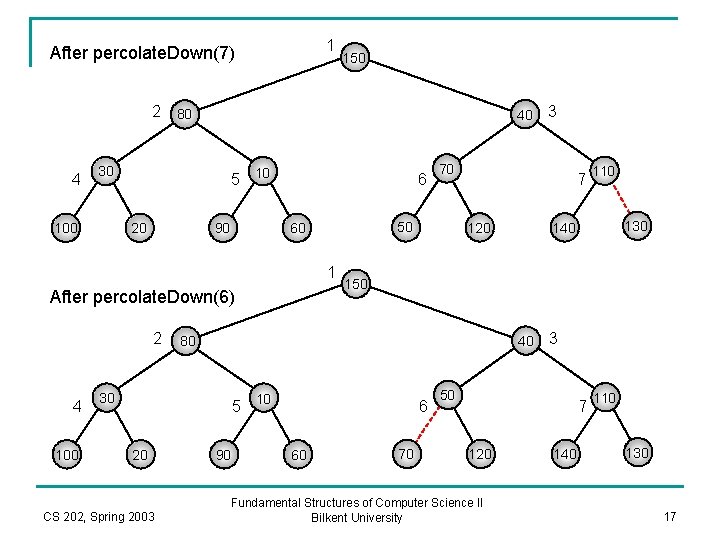
1 After percolate. Down(7) 150 2 80 4 40 30 100 5 10 20 90 6 1 After percolate. Down(6) 2 4 100 120 6 60 130 140 40 90 110 150 5 10 CS 202, Spring 2003 7 80 30 20 70 50 60 3 70 3 50 7 120 Fundamental Structures of Computer Science II Bilkent University 140 110 130 17

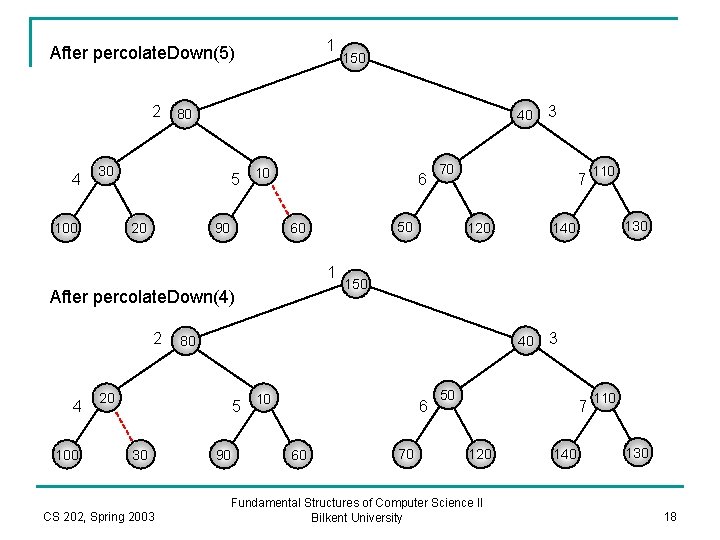
1 After percolate. Down(5) 150 2 80 4 40 30 100 5 10 20 90 6 1 After percolate. Down(4) 2 4 100 120 6 60 130 140 40 90 110 150 5 10 CS 202, Spring 2003 7 80 20 30 70 50 60 3 70 3 50 7 120 Fundamental Structures of Computer Science II Bilkent University 140 110 130 18

1 After percolate. Down(3) 150 2 80 4 40 20 100 5 10 30 90 6 1 After percolate. Down(2) 2 4 100 120 6 80 130 140 40 90 110 150 5 60 CS 202, Spring 2003 7 10 20 30 50 70 60 3 70 3 50 7 120 Fundamental Structures of Computer Science II Bilkent University 140 110 130 19

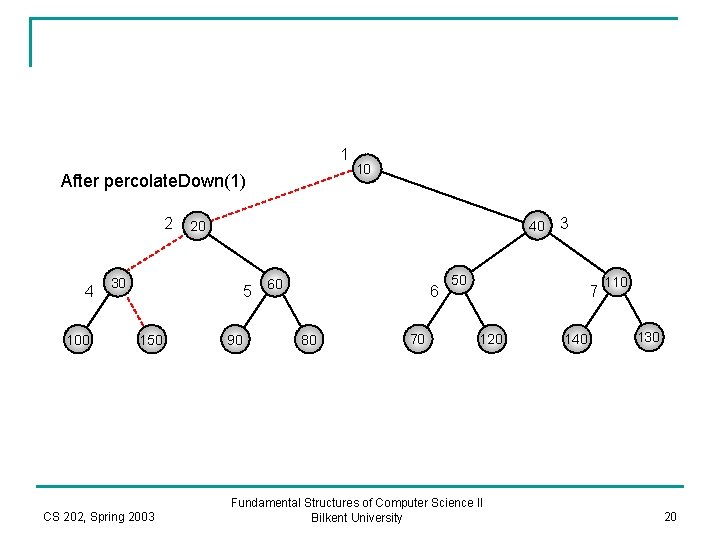
1 After percolate. Down(1) 2 4 100 10 20 40 30 5 60 150 CS 202, Spring 2003 90 6 80 70 3 50 7 120 Fundamental Structures of Computer Science II Bilkent University 140 110 130 20

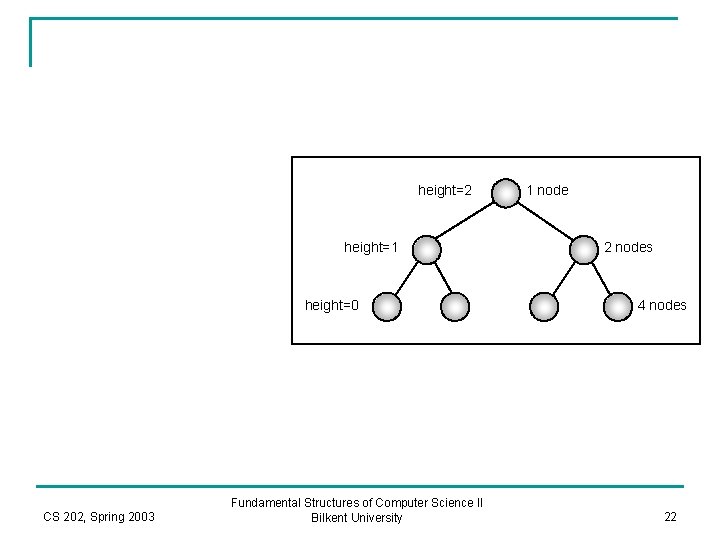
Analysis of Build. Heap n n The cost of Build. Heap is bounded by the number of dashed red lines, which is bounded by the sum of heights of all nodes of the heap. We will show that this sum is O(N), where N is the number of nodes in the heap. CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 21

height=2 height=1 height=0 CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 1 node 2 nodes 4 nodes 22

CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 23

n A complete tree is not a perfect binary tree, but number of nodes in a complete tree of height h is: q n 2 h <= N < 2 h+1 The sum we came up is an upperbound on the sum of height of all nodes in a complete tree. CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 24

Application of Priority Queues n We have talked about application in q q n Operating Systems – scheduling Printer queue Some more applications q Implementation of several graph algorithms n n q Selection Problem … Discrete event simulation CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 25

The Selection Problem n Given a list of N elements and an integer k (1 <= k <= N) q n Find out the kth largest element in the list. Example: q List of elements: 4, 9, 0, 3, 5, 7, 10, 12, 2, 8 n n n 1 st largest element is: 12 10 th largest element is: 0 6 th largest element is: 6 q 12 10 9 8 7 5 4 3 2 0 (sorted order of items) CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 26

The Selection Problem n Some solutions q Alg-1) n n q Sort N elements: O(N 2) (for a simple sort algorithm) Retrieve the kth largest element: O(1) Alg-2) n n n 1. Read k elements into an array: O(k) 2. Sort the elements in the array: O(k 2) 3. For each of the remaining elements: (N-k) q n 3. 1 Compare it to the last element in array, if it is larger than the last element in the array, replace it with the last element and put it into correct spot in the array: O(k) Total Running time: O(k + k 2 + (N-k) * k) = O(Nk). CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 27

The Selection Problem n New algorithms q n They will make use of heaps. A 1 q Assume we want to find the kth smallest element. n n n 1. Read N elements into an array O(N) 2. Apply Build. Heap to the array O(N) 3. Perform k delete. Min operations. O(klog. N) q q q Last operation will five us the kth smallest one. The solution is symmetric for finding kth largest element The total running time is O(N + klog. N) CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 28

The Selection Problem n A 2 q q q Use the idea of Alg-2 At any time maintain a set S of k largest element. We want to find the kth largest element. 1. Read k elements into a heap S (of size k). O(k) 2. For each remaining element (N-k) elements n n n q 2. 1 Compare it with the smallest element (root) in heap S 2. 2 If element is larger than root, then put it into S instead of root. 2. 3 Percolate down the root if necessary. O(logk) Running time = O(k+(N-k)logk) = O(Nlogk). CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 29

d-Heaps n Exactly like a binary heap, except that all nodes have d children 1 q A binary heap is a 2 -heap. 2 5 14 15 CS 202, Spring 2003 6 3 7 8 9 4 10 11 12 13 A 3 -Heap Fundamental Structures of Computer Science II Bilkent University 30

Other Heap Operations n Merge q q Combining two heaps into one. Is not a very simple operation n n O(log. N) cost We will discuss three data structure that will support merge operation efficiently q q q Leftist Heaps Skew Heaps Binomial Queues CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 31

Leftist Heaps n If we use arrays to implement heaps: q q n We will have two input arrays (two heaps). Combining them requires copying one array into an other: O(N) time for equal-sized heaps Therefore, we use a linked data structure (like a binary) to perform merge operation more efficiently. CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 32

Leftist Heaps n A leftist heap has q q n n A structural property An order property Order property is the same with ordinary binary heaps. Structural property is little bit different. CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 33

Leftist Heap Property n Definition: q q q n Null path length, npl(X), of any node X is defined as the length of the shortest path from X to a node without two children. Null path length of a node with zero or one child is 0. Null path length of a NULL node is defined to be -1. Null path length of a node is 1 more than the minimum of the null path lengths of its children. A 1 npl(A) = 1 + min{npl(B), npl(C)} = 1 + min{1, 0} =1+0=1 B 1 D 0 E 0 C 0 F 0 0 G CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 34

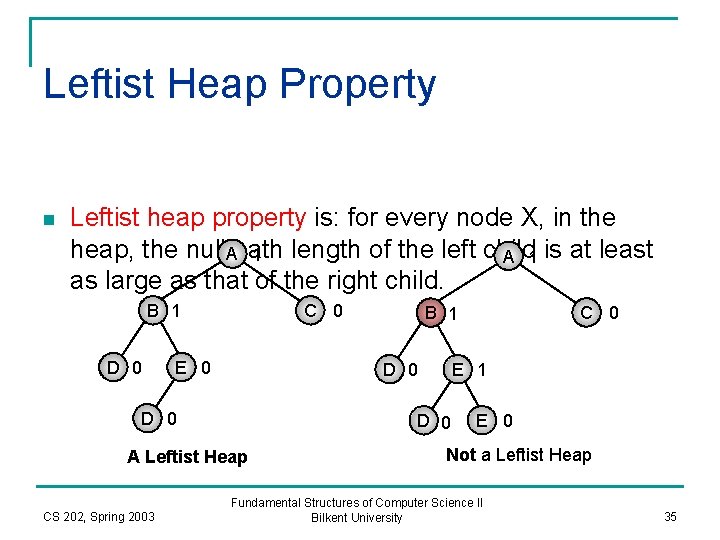
Leftist Heap Property n Leftist heap property is: for every node X, in the heap, the null. Apath length of the left child 1 A 1 is at least as large as that of the right child. B 1 D 0 C 0 E 0 D 0 CS 202, Spring 2003 E 1 D 0 A Leftist Heap C 0 B 1 E 0 Not a Leftist Heap Fundamental Structures of Computer Science II Bilkent University 35

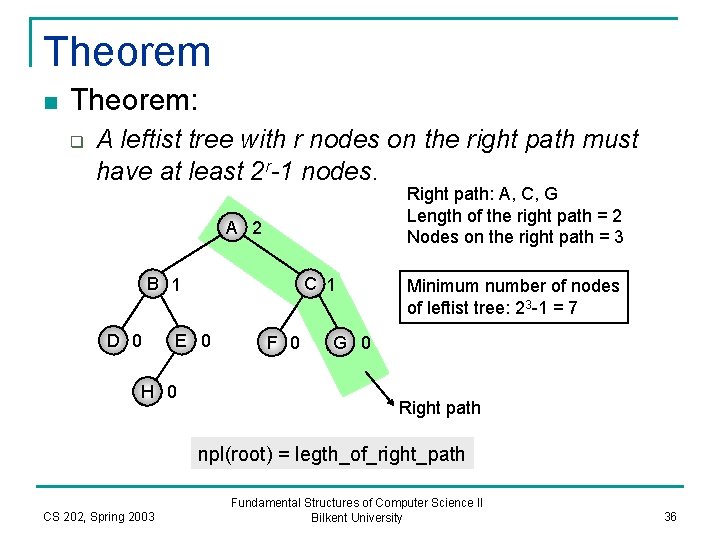
Theorem n Theorem: q A leftist tree with r nodes on the right path must have at least 2 r-1 nodes. Right path: A, C, G Length of the right path = 2 Nodes on the right path = 3 A 2 B 1 D 0 C 1 E 0 H 0 F 0 Minimum number of nodes of leftist tree: 23 -1 = 7 G 0 Right path npl(root) = legth_of_right_path CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 36

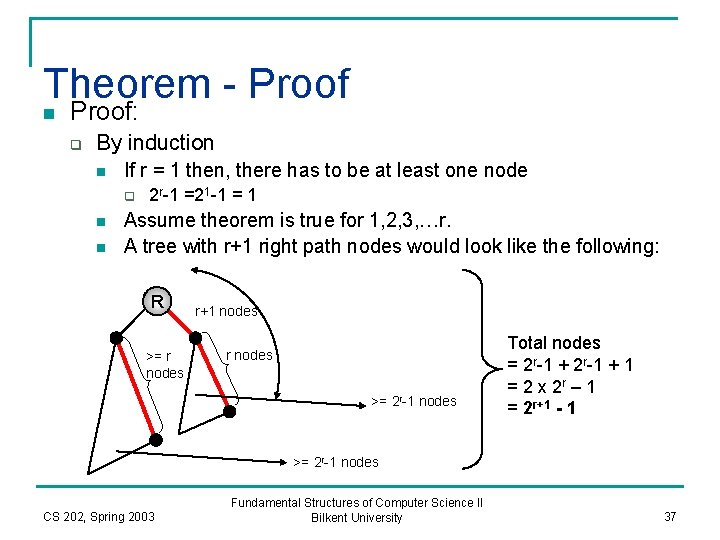
Theorem - Proof n Proof: q By induction n If r = 1 then, there has to be at least one node q n n 2 r-1 =21 -1 = 1 Assume theorem is true for 1, 2, 3, …r. A tree with r+1 right path nodes would look like the following: R >= r nodes r+1 nodes r nodes >= 2 r-1 nodes Total nodes = 2 r-1 + 1 = 2 x 2 r – 1 = 2 r+1 - 1 >= 2 r-1 nodes CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 37

From the previous theorem it follows that the maximum number of nodes in the right path of a leftist heap of size N nodes is: General idea for leftist heap operations is to perform all the work on the right path, which is the shortest. Since, inserts and merges on the right path could destroy the Leftist heap property, we need to restore the property. CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 38

Operations n We will see the following leftist heap operations q Merge n q q Merges two leftist heaps into a single one. Insert Delete. Min CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 39

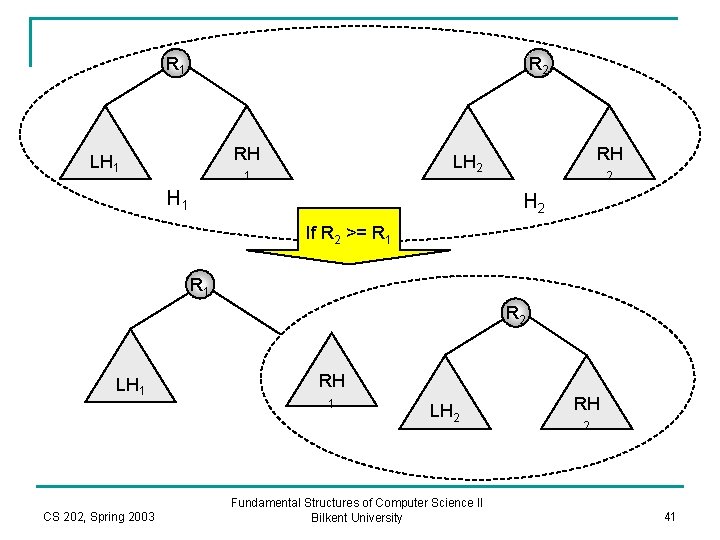
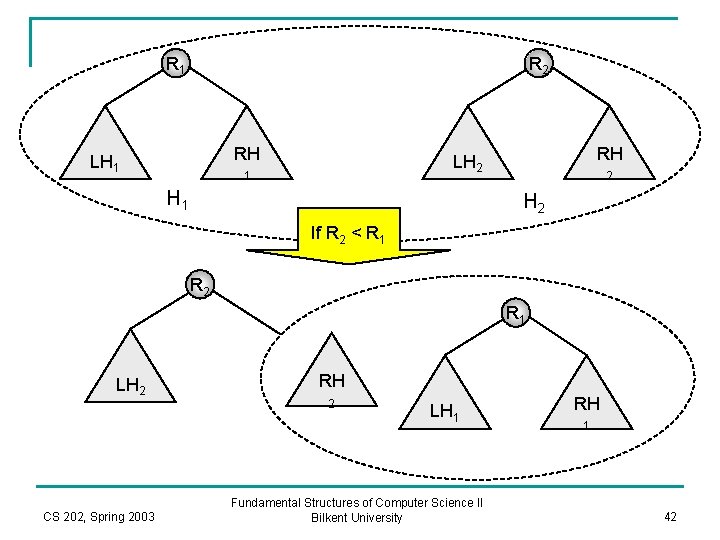
Merge n n Merge two heaps H 1 and H 2. A recursive algorithm q q 1. If either one is empty than it is trivial to merge: return the non-empty heap as the result of merge. 2. Else: n n 2. 1 Merge the heap with the larger root with the right subheap of the heap with the smaller root. (this is ca recursive call) 2. 2 Make the resulting heap as the right child of the heap with the smaller root. Swap the children of the root of the new heap, if npl(rightchild) is greater than npl(left-child). Update npl(root): npl(root) = npl(right-child) + 1; CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 40

R 1 R 2 RH LH 1 RH LH 2 1 H 1 2 H 2 If R 2 >= R 1 R 2 LH 1 CS 202, Spring 2003 RH 1 LH 2 Fundamental Structures of Computer Science II Bilkent University RH 2 41

R 1 R 2 RH LH 1 RH LH 2 1 H 1 2 H 2 If R 2 < R 1 R 2 R 1 LH 2 CS 202, Spring 2003 RH 2 LH 1 Fundamental Structures of Computer Science II Bilkent University RH 1 42

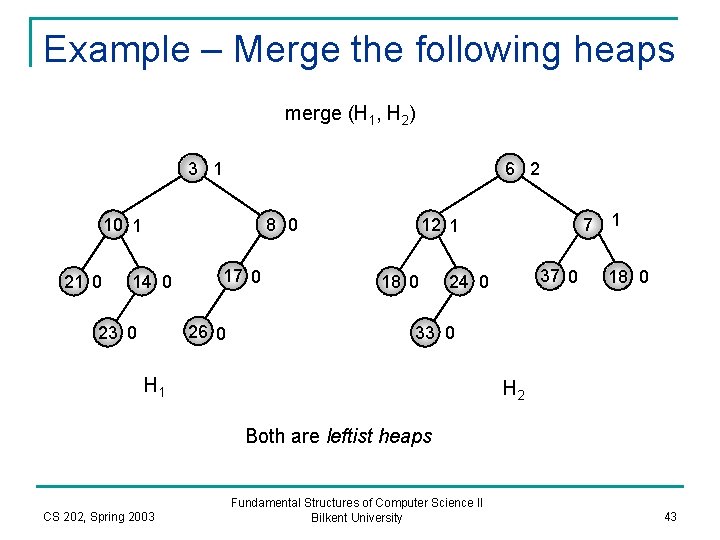
Example – Merge the following heaps merge (H 1, H 2) 3 1 6 2 8 0 10 1 21 0 14 0 17 0 26 0 23 0 7 1 12 1 18 0 37 0 24 0 18 0 33 0 H 1 H 2 Both are leftist heaps CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 43

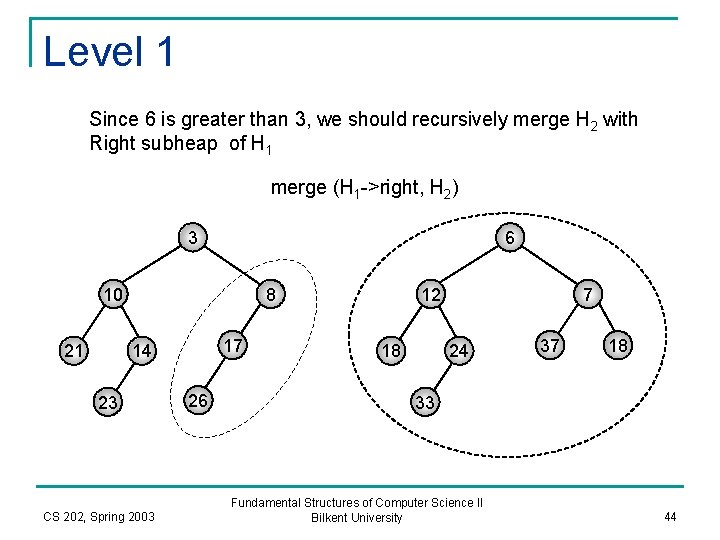
Level 1 Since 6 is greater than 3, we should recursively merge H 2 with Right subheap of H 1 merge (H 1 ->right, H 2) 3 6 10 21 8 17 14 23 CS 202, Spring 2003 26 12 18 7 24 37 18 33 Fundamental Structures of Computer Science II Bilkent University 44

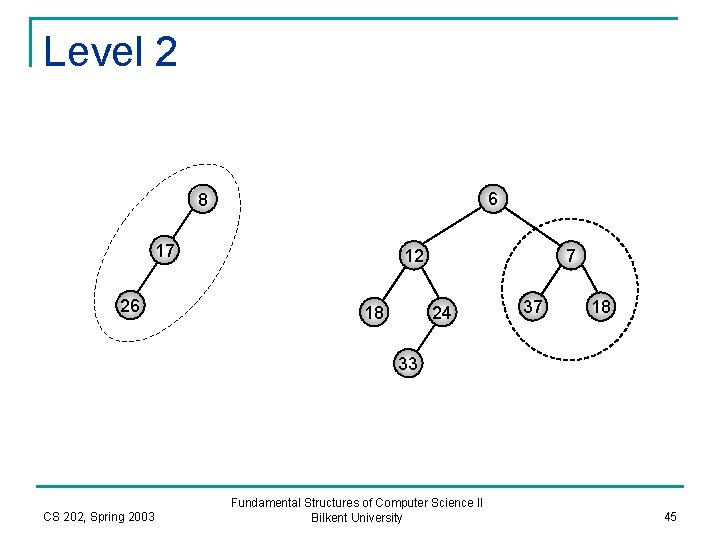
Level 2 6 8 17 26 12 18 7 24 37 18 33 CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 45

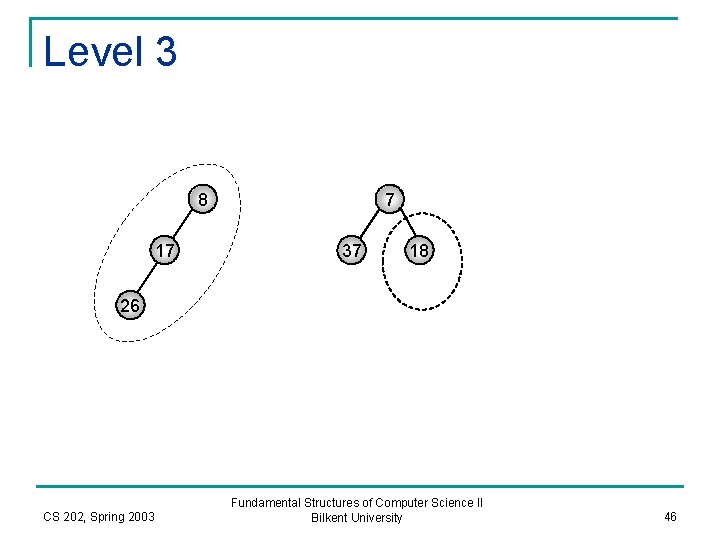
Level 3 8 17 7 37 18 26 CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 46

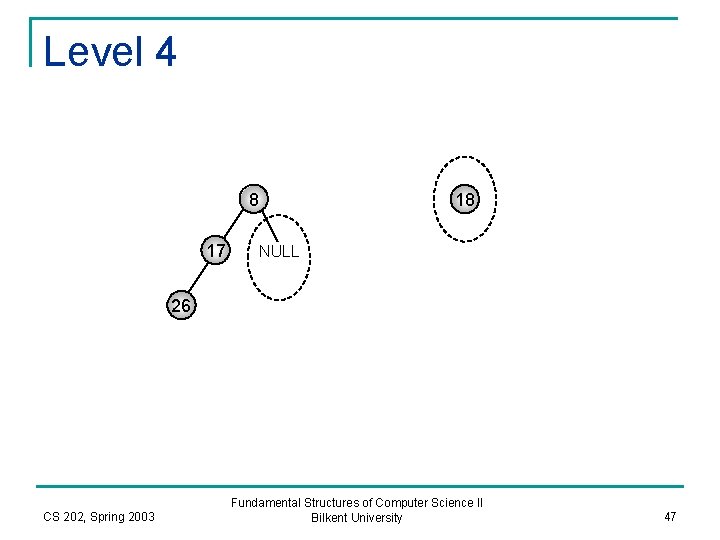
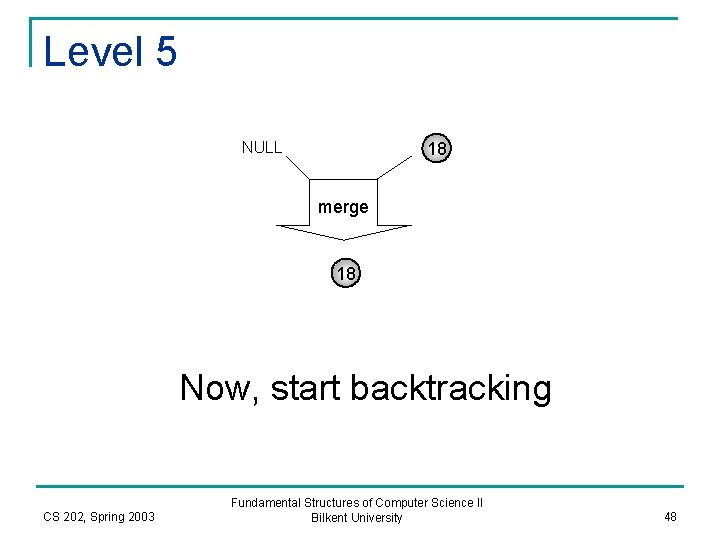
Level 4 8 17 18 NULL 26 CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 47

Level 5 18 NULL merge 18 Now, start backtracking CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 48

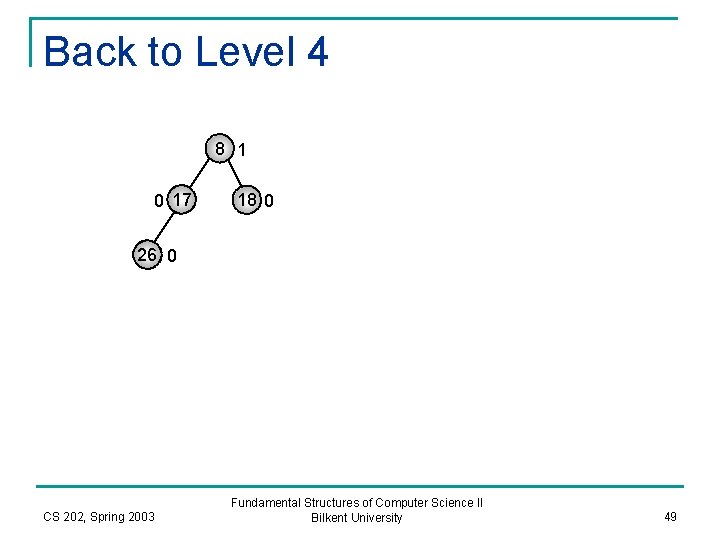
Back to Level 4 8 1 0 17 18 0 26 0 CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 49

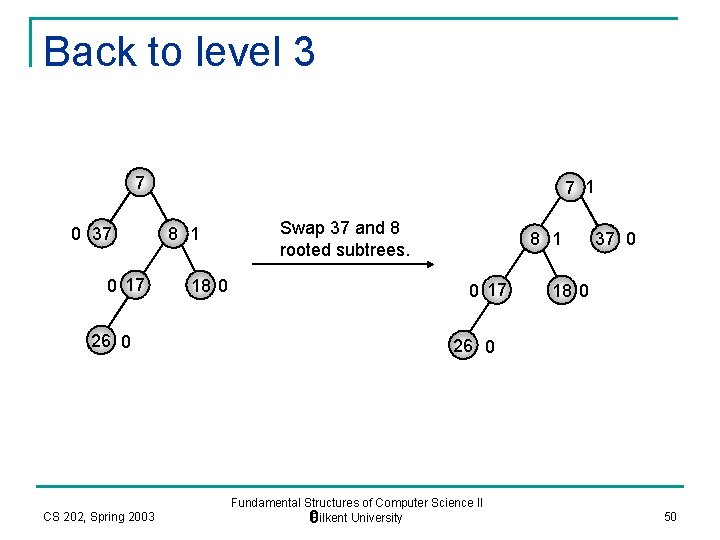
Back to level 3 7 0 37 0 17 26 0 CS 202, Spring 2003 7 1 8 1 18 0 Swap 37 and 8 rooted subtrees. 8 1 0 17 37 0 18 0 26 0 Fundamental Structures of Computer Science II 0 Bilkent University 50

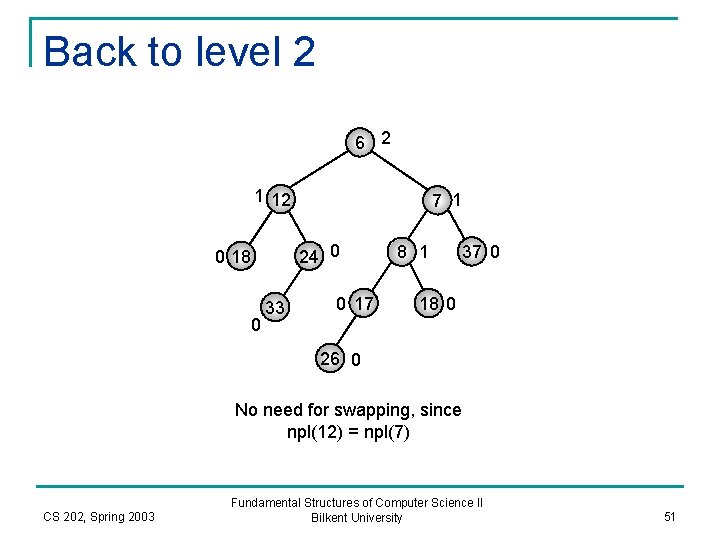
Back to level 2 6 2 1 12 24 0 0 18 0 7 1 33 0 17 8 1 37 0 18 0 26 0 No need for swapping, since npl(12) = npl(7) CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 51

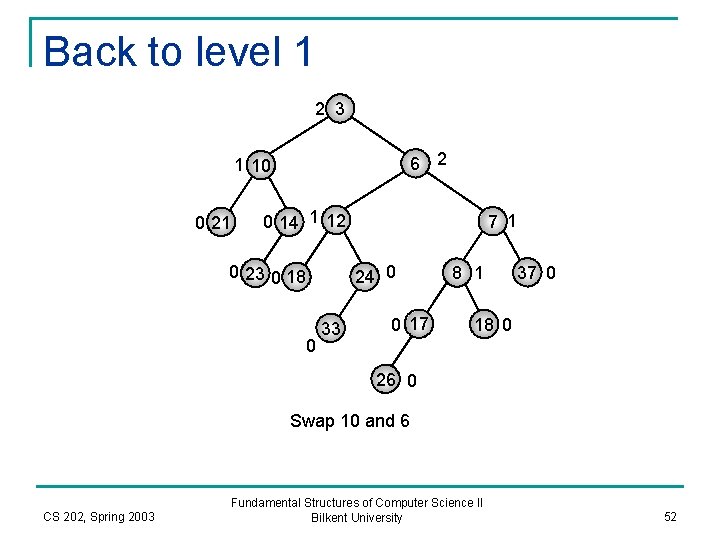
Back to level 1 2 3 6 2 1 10 0 21 0 14 1 12 0 23 0 18 0 7 1 24 0 33 0 17 8 1 37 0 18 0 26 0 Swap 10 and 6 CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 52

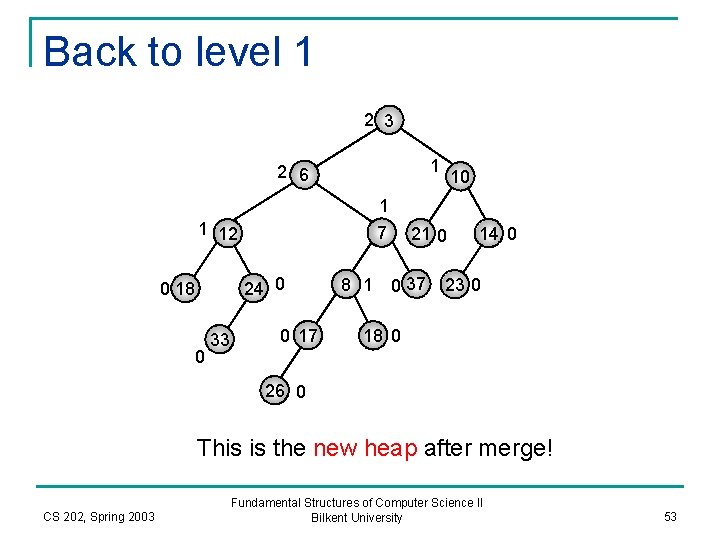
Back to level 1 2 3 1 2 6 10 1 1 12 7 24 0 0 18 0 33 0 17 21 0 8 1 0 37 14 0 23 0 18 0 26 0 This is the new heap after merge! CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 53

Implementation template <class Comparable> class Leftist. Node { Comparable element; Leftist. Node *left; Leftist. Node *right; int npl; }; Leftist. Node( const Comparable & the. Element, Leftist. Node *lt = NULL, Leftist. Node *rt = NULL, int np = 0 ) : element( the. Element ), left( lt ), right( rt ), npl( np ) { } friend class Leftist. Heap<Comparable>; CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 54

template <class Comparable> class Leftist. Heap { public: Leftist. Heap( ); Leftist. Heap( const Leftist. Heap & rhs ); ~Leftist. Heap( ); bool void }; is. Empty( ) const; is. Full( ) const; insert( const Comparable & x ); delete. Min( Comparable & min. Item ); merge( Leftist. Heap & rhs ); private: Leftist. Node<Comparable> *root; /* data member */ Leftist. Node<Comparable> * merge( Leftist. Node<Comparable> *h 1, Leftist. Node<Comparable> *h 2 ) const; Leftist. Node<Comparable> * merge 1( Leftist. Node<Comparable> *h 1, Leftist. Node<Comparable> *h 2 ) const; void swap. Children( Leftist. Node<Comparable> * t ) const; CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 55

// Merge right handside heap into this heap. rhs becomes empty. template <class Comparable> void Leftist. Heap<Comparable>: : merge( Leftist. Heap & rhs ) { if( this == &rhs ) // Avoid aliasing problems return; } root = merge( root, rhs. root ); rhs. root = NULL; CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 56

// calls merge 1 to to actual merge. Makes sure that when merge 1 is called, // h 1 is the node that has smaller root than h 2. template <class Comparable> Leftist. Node<Comparable> * Leftist. Heap<Comparable>: : merge( Leftist. Node<Comparable> * h 1, Leftist. Node<Comparable> * h 2 ) const { if( h 1 == NULL ) return h 2; if( h 2 == NULL ) return h 1; if( h 1 ->element < h 2 ->element ) return merge 1( h 1, h 2 ); else return merge 1( h 2, h 1 ); } CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 57

// assumes heaps are not empty // assumes that h 1 has smaller root. template <class Comparable> Leftist. Node<Comparable> * Leftist. Heap<Comparable>: : merge 1( Leftist. Node<Comparable> * h 1, Leftist. Node<Comparable> * h 2 ) const { if( h 1 ->left == NULL ) // Single node h 1 ->left = h 2; // Other fields in h 1 already accurate else { h 1 ->right = merge( h 1 ->right, h 2 ); if( h 1 ->left->npl < h 1 ->right->npl ) swap. Children( h 1 ); h 1 ->npl = h 1 ->right->npl + 1; } return h 1; } CS 202, Spring 2003 Fundamental Structures of Computer Science II Bilkent University 58