Priority Queue and Binary Heap Neil Tang 02122008

Priority Queue and Binary Heap Neil Tang 02/12/2008 CS 223 Advanced Data Structures and Algorithms 1

Class Overview Ø Priority queue Ø Binary heap Ø Heap operations: insert, delete. Min, de/increase. Key, delete, build. Heap Ø Application CS 223 Advanced Data Structures and Algorithms 2

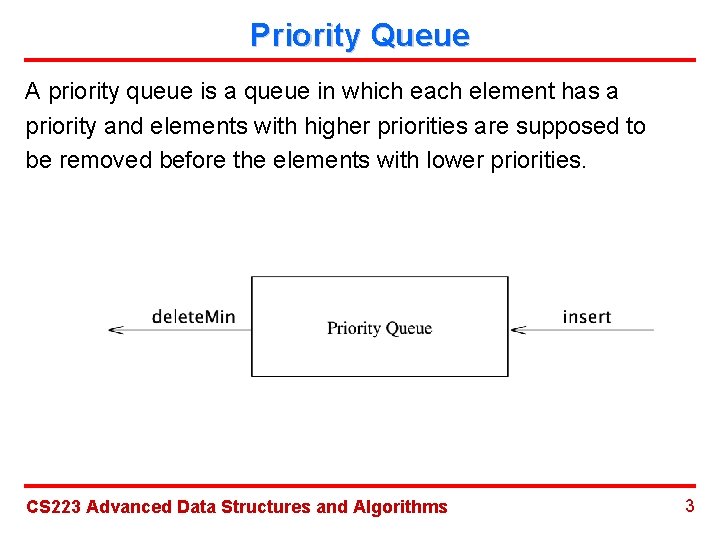
Priority Queue A priority queue is a queue in which each element has a priority and elements with higher priorities are supposed to be removed before the elements with lower priorities. CS 223 Advanced Data Structures and Algorithms 3

Possible Solutions Ø Linked list: Insert at the front (O(1)) and traverse the list to delete (O(N)). Ø Linked list: Keep it always sorted. traverse the list to insert (O(N)) and delete the first element (O(1)). Ø Binary search tree CS 223 Advanced Data Structures and Algorithms 4

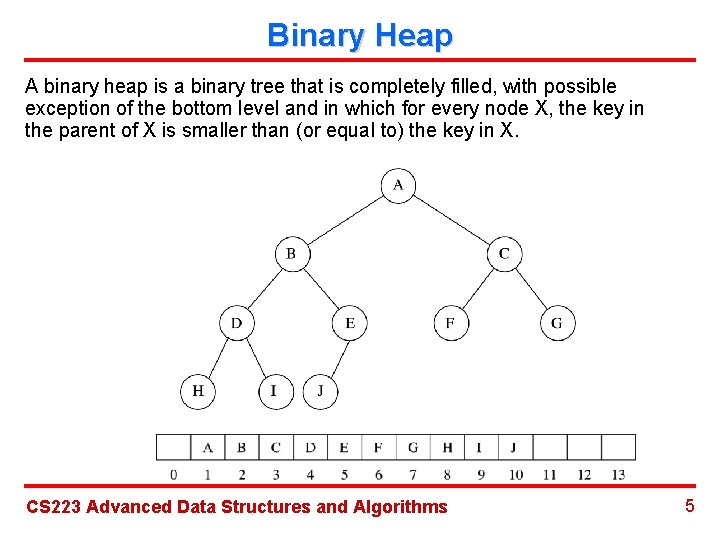
Binary Heap A binary heap is a binary tree that is completely filled, with possible exception of the bottom level and in which for every node X, the key in the parent of X is smaller than (or equal to) the key in X. CS 223 Advanced Data Structures and Algorithms 5

Binary Heap Ø A complete binary tree of height h has between 2 h and 2 h+1 -1 nodes. So h = log. N. Ø For any element in array position i, its left child in position 2 i and the right child is in position (2 i+1), and the parent is in i/2. CS 223 Advanced Data Structures and Algorithms 6

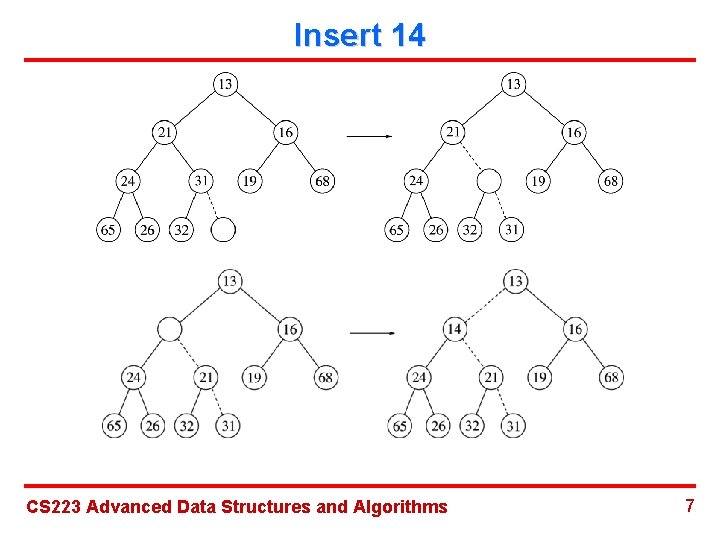
Insert 14 CS 223 Advanced Data Structures and Algorithms 7

Insert (Percolate Up) Time complexity: O(log. N) CS 223 Advanced Data Structures and Algorithms 8

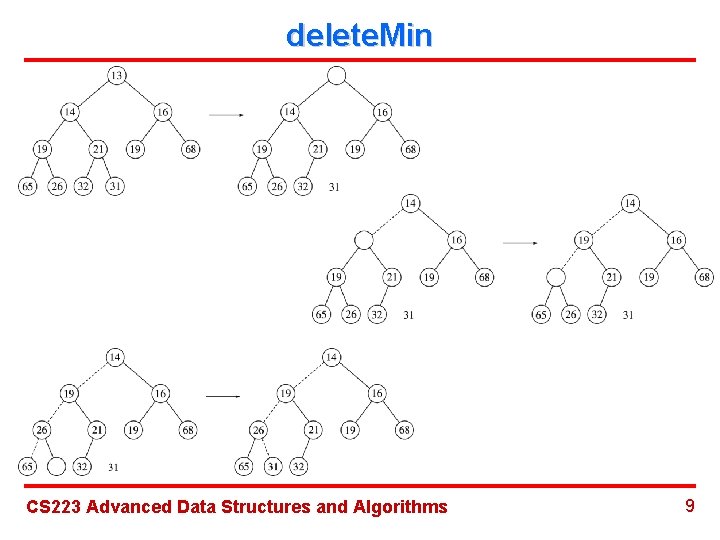
delete. Min CS 223 Advanced Data Structures and Algorithms 9

delete. Min (Percolate Down) Time complexity: O(log. N) CS 223 Advanced Data Structures and Algorithms 10

Other Operations Ø decrease. Key(p, ) Ø increase. Key(p, ) Ø delete(p)? Ø delete(p)=decrease. Key(p, )+delete. Min() CS 223 Advanced Data Structures and Algorithms 11

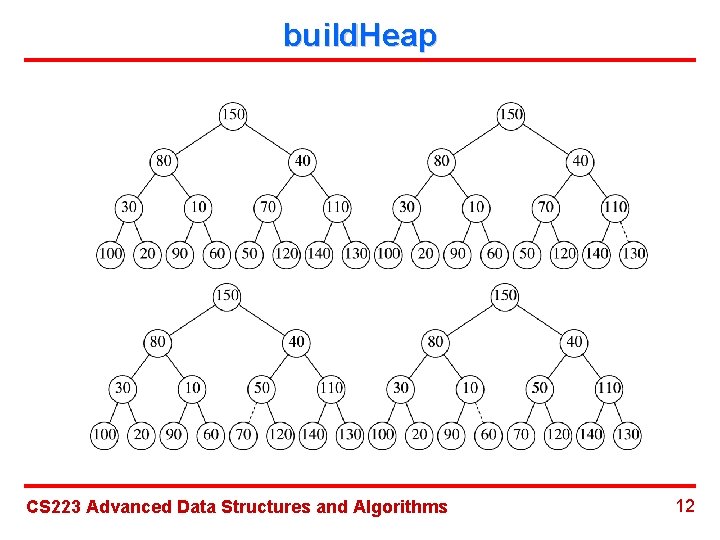
build. Heap CS 223 Advanced Data Structures and Algorithms 12

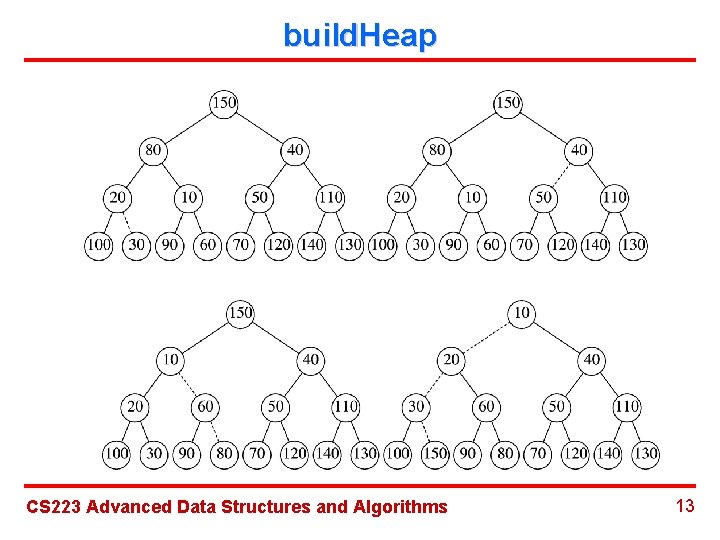
build. Heap CS 223 Advanced Data Structures and Algorithms 13

build. Heap CS 223 Advanced Data Structures and Algorithms 14

build. Heap Ø Theorem: For the perfect binary tree of height 2 h+1 -1 nodes the sum of the heights of the nodes is 2 h+1 -1 -(h+1). Ø Time complexity: 2*(2 h+1 -1 -(h+1)) = O(N). CS 223 Advanced Data Structures and Algorithms 15

Applications Ø Problem: find the kth smallest element. Ø Algorithm: build. Heap, then delete. Min k times. Ø Time complexity: O(N+klog. N) = O(Nlog. N). CS 223 Advanced Data Structures and Algorithms 16

Applications Ø Problem: find the kth largest element. Ø Algorithm: build. Heap with the first k elements, check the rest one by one. In each step, if the new element is larger, delete. Min and insert the new one. Ø Time complexity: O(k+(N-k)logk) = O(Nlog. N). CS 223 Advanced Data Structures and Algorithms 17