Principles to Actions Effective Mathematics Teaching Practices The

Principles to Actions Effective Mathematics Teaching Practices The Case of Kelly Polosky and the Triangle Task Fifth Grade Developed by Michael D. Steele at the University of Wisconsin-Milwaukee. Video courtesy of the Wilkinsburg School District and the Institute for Learning. These materials are part of the Principles to Actions Professional Learning Toolkit: Teaching and Learning created by the project team that includes: Margaret Smith (chair), Victoria Bill (co-chair), Melissa Boston, Fredrick Dillon, Amy Hillen, De. Ann Huinker, Stephen Miller, Lynn Raith, and Michael Steele.

Overview of the Session • Solve and Discuss the Triangle Task • Watch video clips and discuss what the teacher does to support her students’ engagement in and understanding of mathematics • Discuss the effective mathematics teaching practices of procedural fluency from conceptual understanding

The Triangle Task Using the triangles shown above and the grid paper, construct a formula for the area of a right triangle. You may cut your triangles out and manipulate them in any way that might help you make your argument. After you explore with your particular triangle, make a general mathematical argument using words, symbols, and diagrams about the formula for the area of any right triangle. Task adapted from Everyday Mathematics Grade 5, Copyright © 2007 by Wright Group/Mc. Graw-Hill, Chicago.

The Triangle Task Video School District: School: Coach: Teacher: Class: Curriculum: Wilkinsburg Kelly Elementary School Darin Cole Ms. Kelly Polosky 5 th grade Everyday Mathematics This small district is adjacent to the City of Pittsburgh and features a diverse student body. A coach, Mr. Cole, is also present in the video interacting with students. The students have just begun the geometry unit. Prior to the day’s lesson, the students sorted polygons and non-polygons and they identified the characteristics of polygons. They have also found the formulas for the area of rectangles and squares.

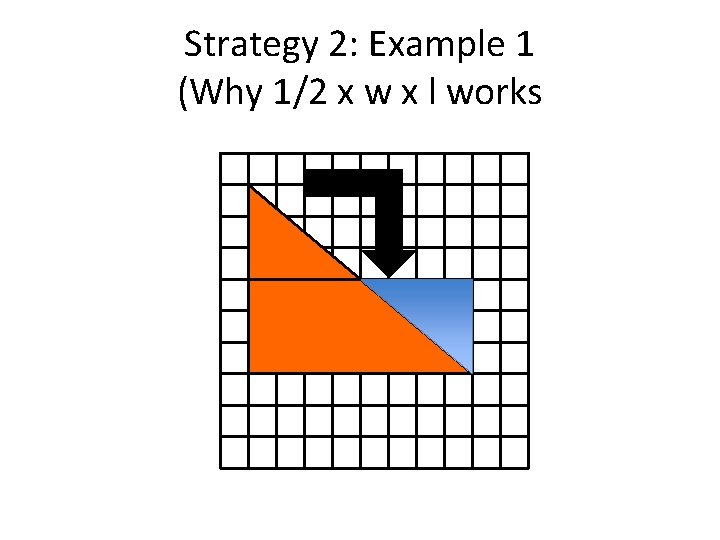
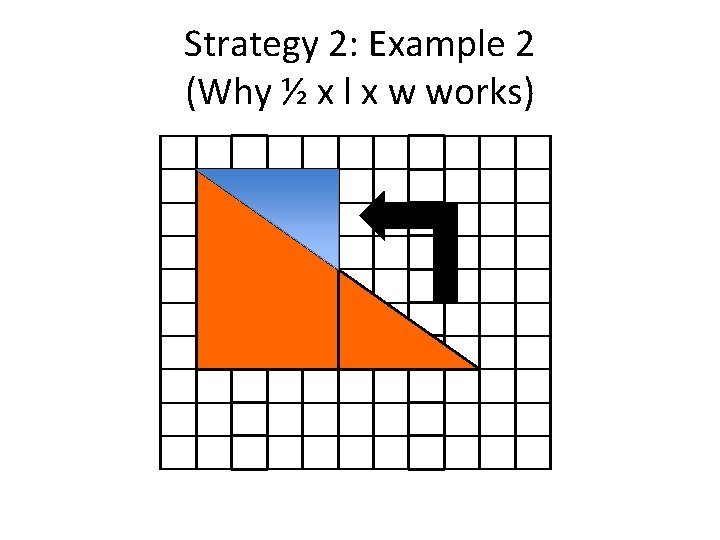
Ms. Polosky’s Mathematics Learning Goals Students will understand that: 1. The area of a triangle is ½ of its length times its width. 2. The relationship between area, length and width of a triangle can be generalized to a formula. 3. There are several equivalent ways of writing the formula for the area of a triangle and each can be related to a physical model.

Connections to the CCSS Content Standards Geometry★ 6. G Solve real-world and mathematical problems involving area, surface area, and volume. 1. Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems. National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards for mathematics. Washington, DC: Authors.

Connections to the CCSS Standards for Mathematical Practice 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. 8. Look for and express regularity in repeated reasoning.

The Triangle Task: Video Context Prior to this clip: • Ms. Polosky launched the task, ensuring that students understood what they were being asked to do • Ms. Polosky provided students with cardboard triangles and other tools such as scissors and grid paper In this clip, we see Ms. Polosky facilitating a wholeclass discussion that focused on comparing two possible formulas for the area of a right triangle generated by students.

Lens for Watching the Video Time 1 As you watch the video, make note of what the teacher does to support student learning and engagement as they work on the task. In particular, identify any of the Effective Mathematics Teaching Practices that you notice Ms. Polosky using. Be prepared to give examples and to cite line numbers from the transcript to support your claims.

Effective Mathematics Teaching Practices 1. 2. 3. 4. 5. 6. 7. 8. Establish mathematics goals to focus learning. Implement tasks that promote reasoning and problem solving. Use and connect mathematical representations. Facilitate meaningful mathematical discourse. Pose purposeful questions. Build procedural fluency from conceptual understanding. Support productive struggle in learning mathematics. Elicit and use evidence of student thinking.

Procedural Fluency from Conceptual Understanding Mathematics classrooms should: • Provide students opportunities to use their own reasoning strategies and methods to solve problems; • Press students to explain and discuss why the procedures they are using work for particular problems; • Use visual models to support students’ understandings of general methods To use mathematics effectively, students must be able to do much more than carry out mathematical procedures. They must know which procedure is appropriate and most productive in a given situation, what a procedure accomplishes, and what kind of results to expect. Mechanical execution of procedures without understanding their mathematical basis often leads to bizarre results. (Martin, 2009, p. 165)

Lens for Watching the Video: Time 2 As you watch the video a second time, make note specifically of how you see Ms. Polosky supporting students in developing procedural fluency from conceptual understanding. Be prepared to give examples and to cite line numbers from the transcript to support your claims.

Effective Mathematics Teaching Practices 1. 2. 3. 4. 5. 6. 7. 8. Establish mathematics goals to focus learning. Implement tasks that promote reasoning and problem solving. Use and connect mathematical representations. Facilitate meaningful mathematical discourse. Pose purposeful questions. Build procedural fluency from conceptual understanding. Support productive struggle in learning mathematics. Elicit and use evidence of student thinking.

Connecting Conceptual and Procedural Knowledge Imagine that following the this lesson, Ms. Polosky engages her students in solving real-world tasks using area. For Tasks A-D, consider: • • Which tasks might support Ms. Polosky’s students in advancing from a generalization for right triangles to a generalization for all triangles? What aspects of the tasks provided might be challenging for her students to solve, and why?

Connecting Conceptual and Procedural Knowledge Consider Task B. If Task B were the type of task that Ms. Polosky would want students to be procedurally fluent in solving as a part of an assessment, what aspects of conceptual understanding would help support that fluency? How might a teacher foster those aspects of understanding?

Consider the Teacher and Student Actions Related to Developing Procedural Fluency from Conceptual Understanding • What will you need to work on in order to develop procedural fluency from conceptual understanding in your own classroom? • Where will you start?

Build Procedural Fluency from Conceptual Understanding Teacher and Student Actions What are teachers doing? • Using visual models to support students’ understanding of general methods. • Providing students with opportunities for distributed practice of procedures. What are students doing? • Striving to use procedures appropriately and efficiently.

Strategy 2: Example 1 (Why 1/2 x w x l works

Strategy 2: Example 2 (Why ½ x l x w works)