Principles of Radar Tracking Using the Kalman Filter

Principles of Radar Tracking Using the Kalman Filter to locate targets copyright 2006 free template from brainybetty. com

Abstract Problem-Tracking moving targets, minimize radar noise Solution-Use the Kalman Filter to largely eliminate noise when determining the velocities and distances

Noise • Error (noise) is described by an ellipse – Defined by variance and covariance in x and y • Two kinds of error – State – Measurement

Teams Reciproverse Brian Dai Joshua Newman Michael Sobin Lexten Stephen Chan Adam Lloyd Jonathan Mac. Millan Alex Morrison

History of the Kalman Filter • Problem: 1960’s, Apollo command capsule • Dr. Kalman and Dr. Bucy – Make highly adaptable iterative algorithm – No previous data storage – Estimates non-measured quantities (velocity) • Later found to be useful for other applications, such as air traffic control Dr. Kalman

Model xykk: : position and velocity of the target measurement at time(state) k at (k+1 gets is next time step) in X H: time termkthat rid of velocity Φ: state transitionnoise, matrixdictated by our devices r: measurement qk: uncertainty in the state due to “noise” (e. g. wind variation and pilot error)

Other Important Matrices • P: error covariance matrix – Describes estimate accuracy • K: Kalman gain matrix – Intermediate weighting factor between measured and predicted • I: identity matrix

Some Matrices

Kalman Filter: Predict

Kalman Filter: Correct

Tools: Visual Basic • Matlib- an external matrix operations library • Input format – text files, simulated radar data • Console- data output

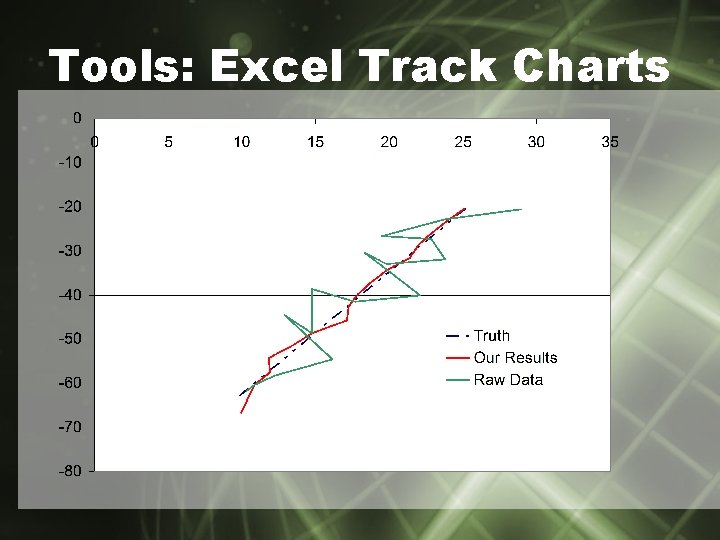
Tools: Excel Track Charts

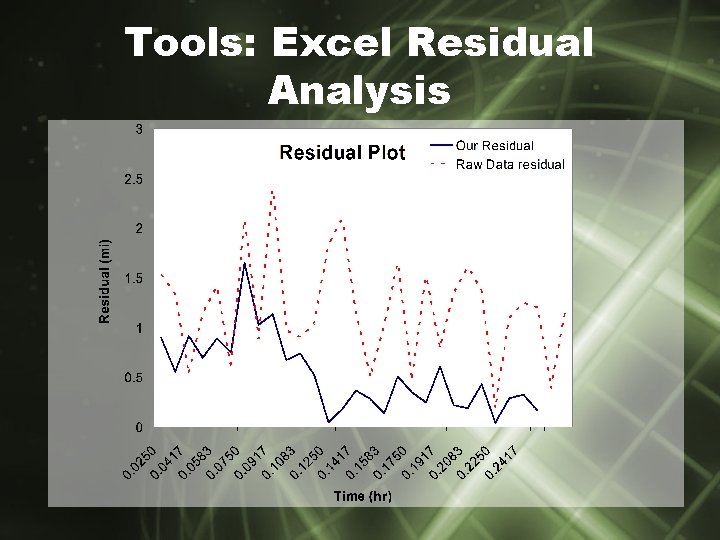
Tools: Excel Residual Analysis

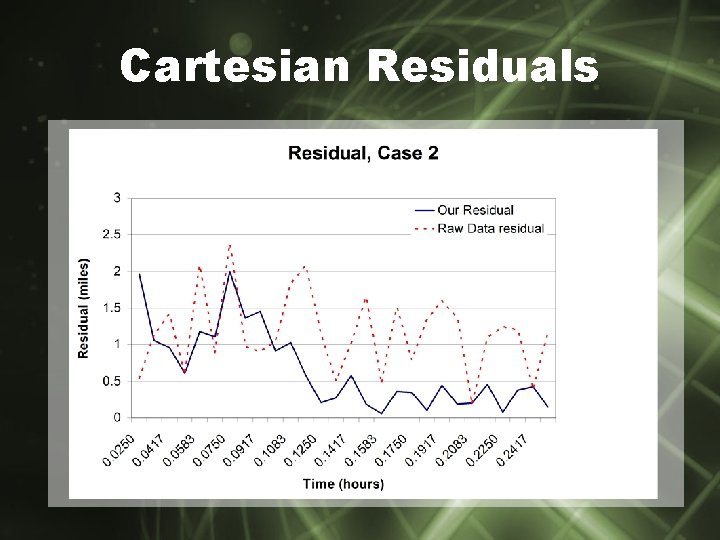
Filter Development: Cartesian Coordinates • Filter Implemented • Test: Residual Analysis • Does it work?

Cartesian Residuals

Filter Development: Polar Coordinates • Prefiltering • Polar to Cartesian conversion • More appropriate data feed • Error matrices – Redefine R

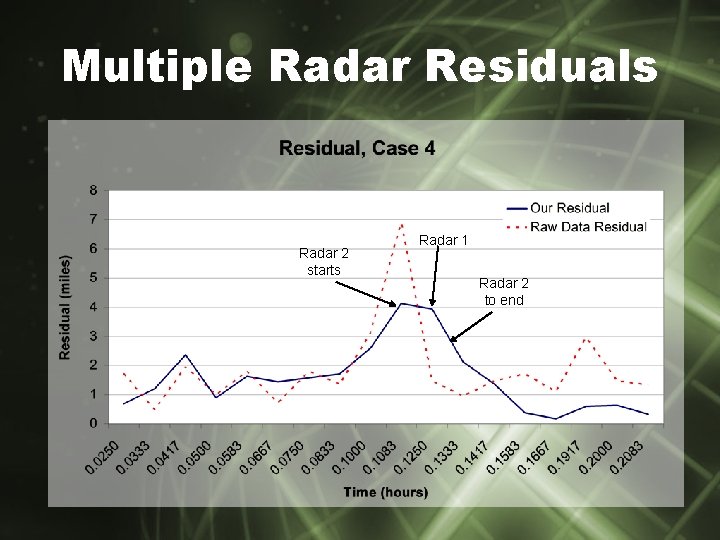
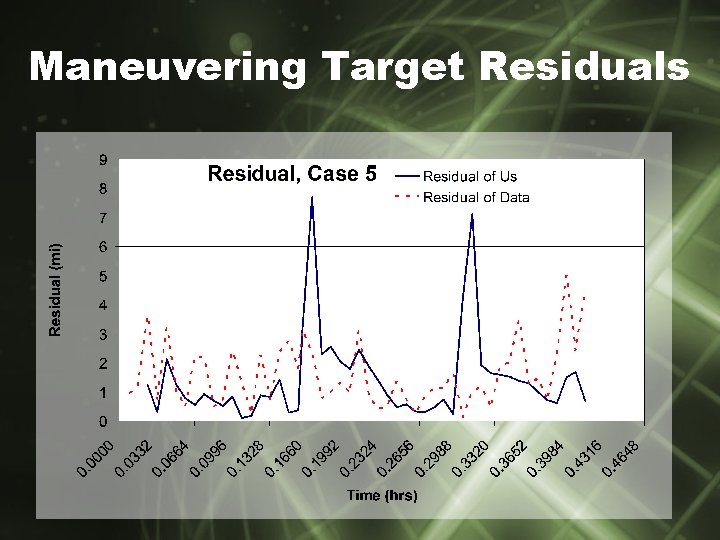
Filter Development: Multiple Radars • Mapping coordinates to absolute coordinate plane • Two radars means a smaller error ellipse • Note drop in residual – Switch to second radar

Multiple Radar Residuals Radar 2 starts Radar 1 Radar 2 to end

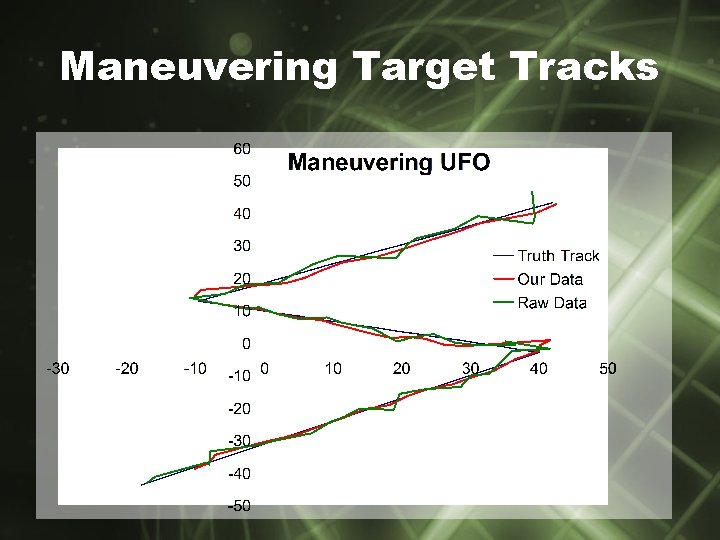
Maneuvering Targets • Filter Reinitialization – 3σ error ellipse (~98%) – If three consecutive data points outside ellipse, reinitialize filter – Should happen upon maneuvering • Prevents biased prediction matrix 3σ GOOD Predicted point BAD

Maneuvering Target Tracks

Maneuvering Target Residuals

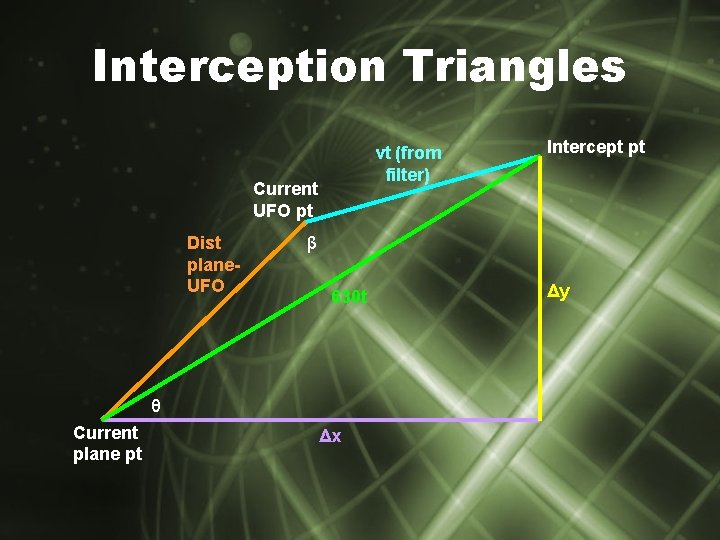
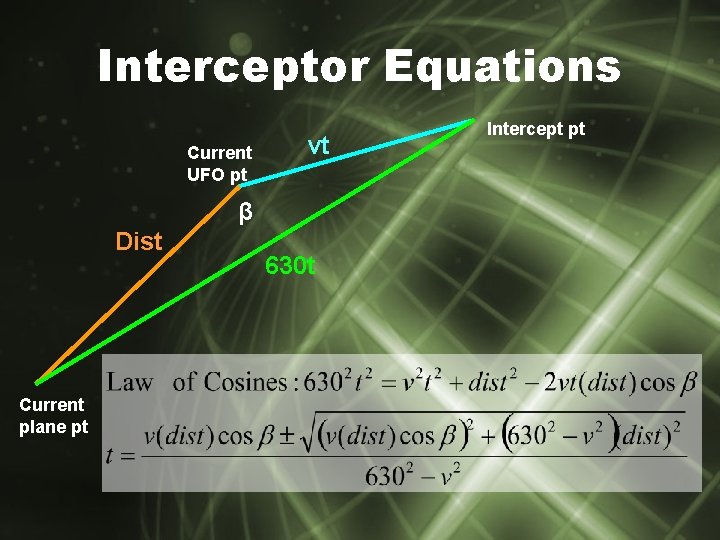
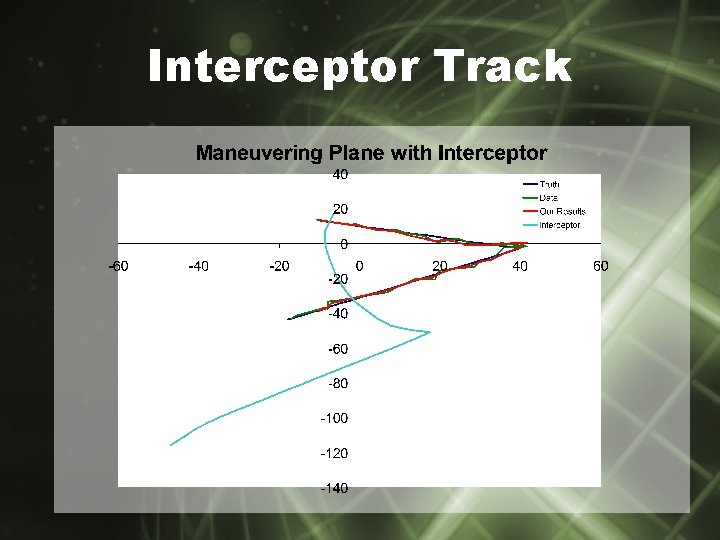
Interception • Give interceptor path using filter – Interceptor: constant velocity – Intercept UFO • Cross target path before designated time • Solve using Law of Cosines

Interception Triangles vt (from filter) Current UFO pt Dist plane. UFO β 630 t θ Current plane pt Intercept pt Δx Δy

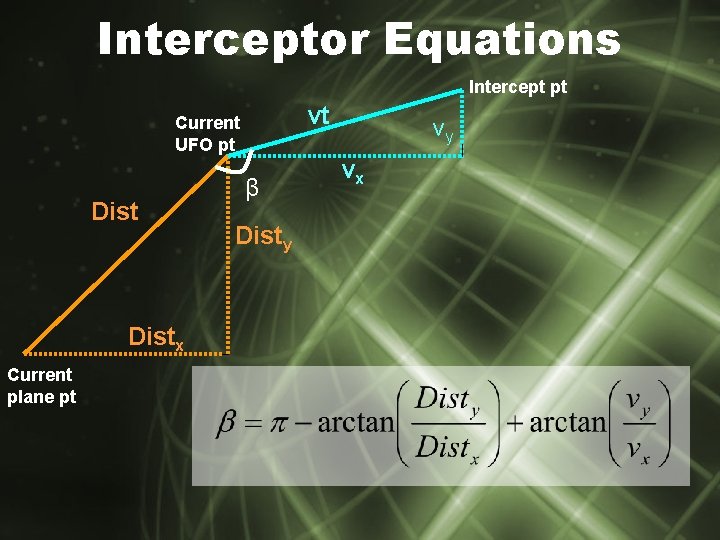
Interceptor Equations Intercept pt vt Current UFO pt Distx Current plane pt β Disty vy vx

Interceptor Equations Current UFO pt vt β Dist Current plane pt 630 t Intercept pt

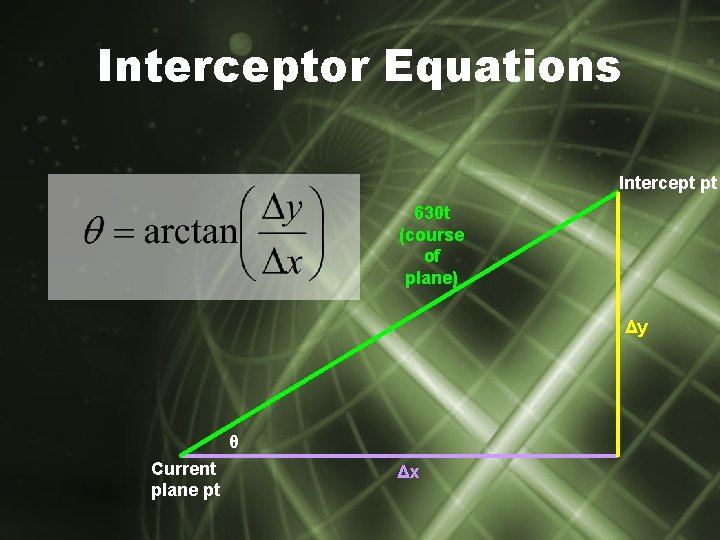
Interceptor Equations Intercept pt 630 t (course of plane) Δy θ Current plane pt Δx

Interceptor Track

Multiple Targets • Tracking multiple targets lends itself to an object oriented approach • Why is it useful? Collision avoidance Target Class Methods: Matrices • Initialize • X • Predict • Y • Correct • P • R Target Object

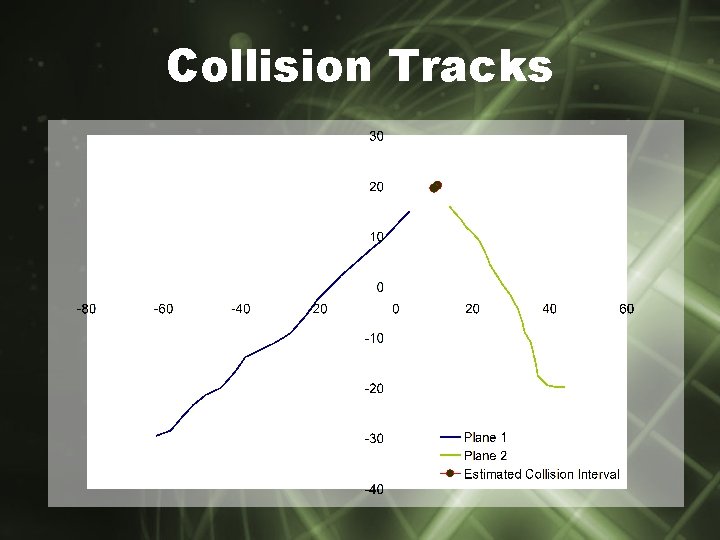
Collision Avoidance

Collision Avoidance Math Express position at a future time t: Plane 1: Plane 2:

Collision Avoidance Math Determine if planes will be within one mile at any such time: Make some substitutions to simplify the expression:

Collision Avoidance Math Arrive at inequality describing dangerous time interval: The solution to this inequality is the time interval when the planes will be in danger

Collision Tracks

Conclusion • Using the Kalman filter, we were able to minimize radar noise and analyze target tracking scenarios. • We solved: plane collision avoidance, interception, tracking multiple aircraft • Still relevant today: several space telescopes use the Kalman Filter as a low powered tracking device

Acknowledgements • • • Mr. Randy Heuer Zack Vogel Dr. Paul Quinn Dr. Miyamoto Ms. Myrna Papier NJGSS ’ 07 Sponsors

Works Cited • http: //www. physics. utah. edu/~detar/phy cs 6720/handouts/curve_fit/img 147. gif • http: //www. afrlhorizons. com/Briefs/Mar 02/OSR 0106. html • http: //www. cs. unc. edu/~welch/kalman/ media/images/kalman-new. jpg • http: //www. combinatorics. org/Surveys/ ds 5/gifs/5 -VD-ellipses-labelled. gif