Principles of Radar Target Tracking The Kalman Filter

Problems with Radar n n Radar can’t measure velocity Radar has measurement error: “noise”

Purpose of Kalman Filter Transform data input from radar trackers into usable form n

Rudolph Kalman n n Rudolph E. Kalman was the “inventor” of the Kalman Filter

Overview of Kalman Filter Initialize Matrices Read Data Predict Correct Measurement Covariance Update Output

Introduction to Project n Part 1 n n 2 Team Scenario, competing for government

Problems Getting Started Problems Solutions n New programming language n Looked at help files

Kalman Model n State Model n Measurement Model

Programming Made using Visual Basic. NET n Read data file n Convert coordinates n

Case Studies: Basic Kalman Filter noise from a basic, linear data n Limited functionality,

Case Studies: How to Read Graphs n Data Analysis n n n Comparison of

Case Studies: Filter with Polar Coordinates Data inputted in range and bearing n Challenges

Case Studies: Filter with Polar Coordinates n n n Filter incorporates past and current

Case Studies: Filter with Polar Coordinates

Case Studies: Multiple Targets n n n Code rewrite necessary Object-oriented rather than structured

Case Studies: Collision Avoidance n n n Use data on multiple targets Predict collisions

Case Studies: Maneuver Detection n Comparison of projected path and measured data When target

Case Studies: Interceptor n n n Includes maneuver detection algorithms Direct interceptor towards earliest

Conclusion Visual Basic. NET successfully handled the Kalman equations n Kalman Filter successfully reduced

References n n n [IEEE] Institute of Electrical and Electronics Engineers. 2003 Jan 23.

Slides: 31

Download presentation

Principles of Radar Target Tracking The Kalman Filter: Mathematical Radar Analysis

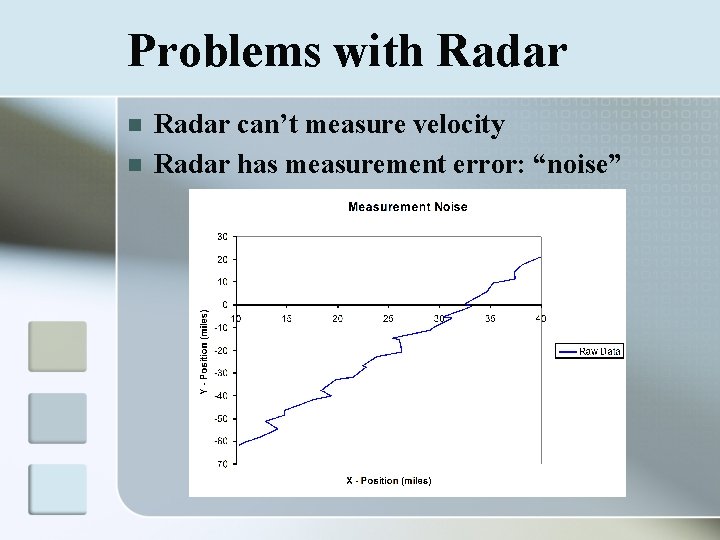
Problems with Radar n n Radar can’t measure velocity Radar has measurement error: “noise”

Purpose of Kalman Filter Transform data input from radar trackers into usable form n Reduce measurement error (“noise”) of target’s position and velocity n Predict future state of target using previous state estimate and new data n Lightweight, robust, and expandable program n

Rudolph Kalman n n Rudolph E. Kalman was the “inventor” of the Kalman Filter Began research on control theory in 1958 Blended earlier works Worked with partner R. S. Bucy http: //www. rpi. edu/~kracua/seminar/det. html

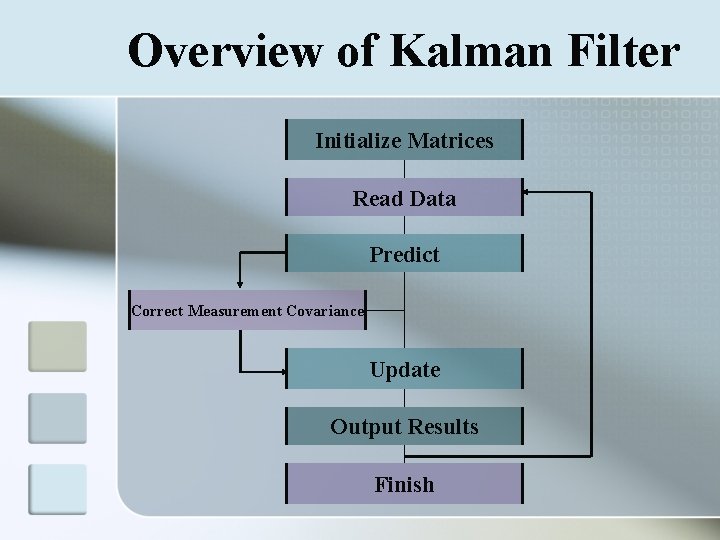
Overview of Kalman Filter Initialize Matrices Read Data Predict Correct Measurement Covariance Update Output Results Finish

Introduction to Project n Part 1 n n 2 Team Scenario, competing for government contract Similar Projects Individual Programs, Analyses, Graphs required Part 2 n n Teams Merge Written Component

Problems Getting Started Problems Solutions n New programming language n Looked at help files and API’s n Unfamiliar algorithm n Teamwork in research n Matrix Algebra n Matrix library

Kalman Model n State Model n Measurement Model

Steps of Kalman Filter n Predict

Steps of Kalman Filter n Correct

Programming Made using Visual Basic. NET n Read data file n Convert coordinates n Predict location n Output to Excel n Graph flight path n

Case Studies: Basic Kalman Filter noise from a basic, linear data n Limited functionality, based solely on Cartesian coordinates n Built to be expandable, adaptable n Challenges n n First experience with Kalman Filter tracking

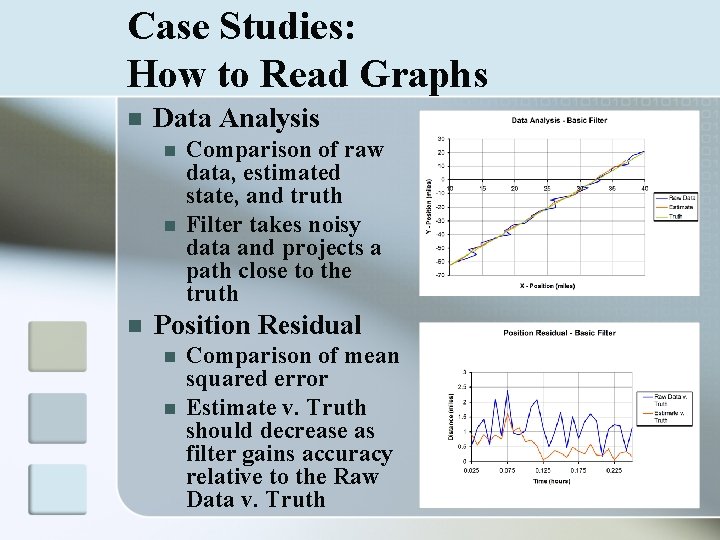
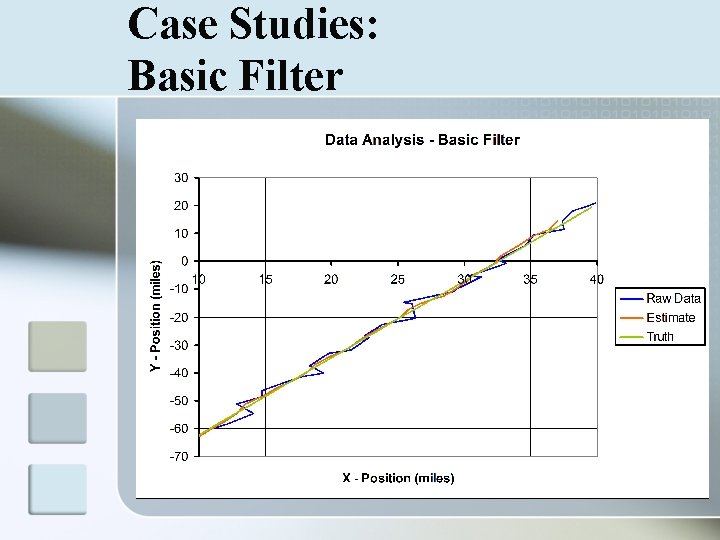
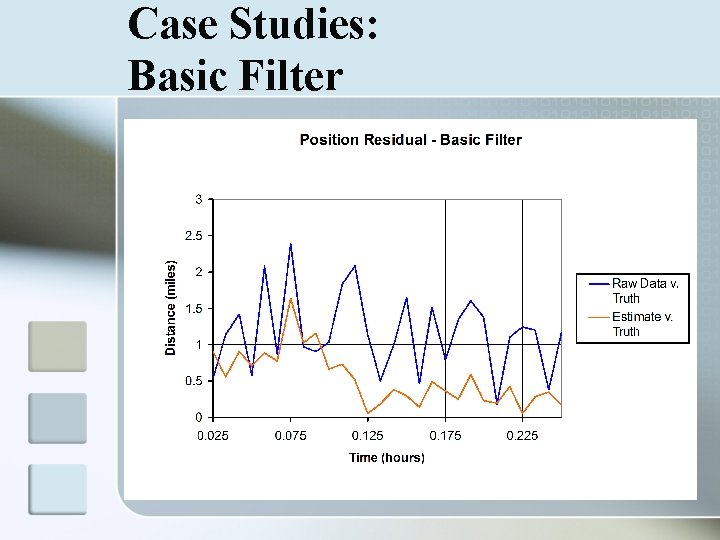
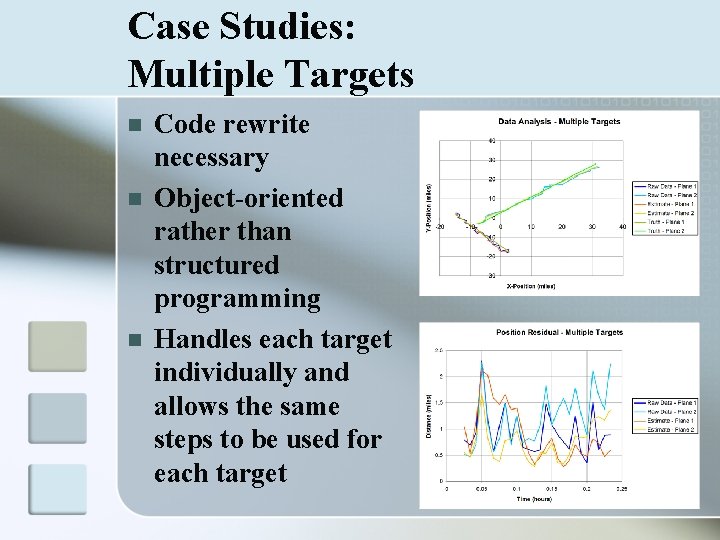
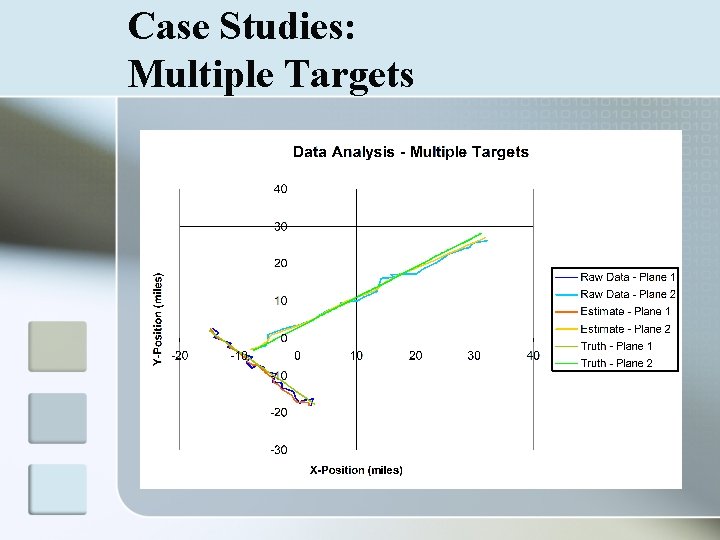
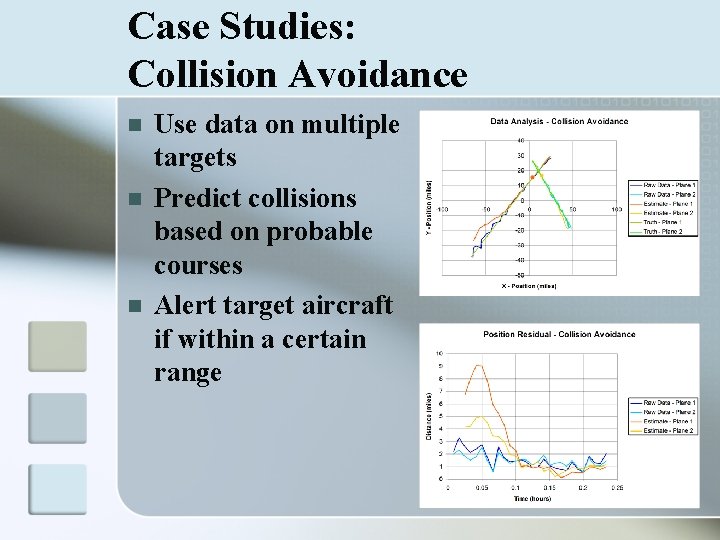
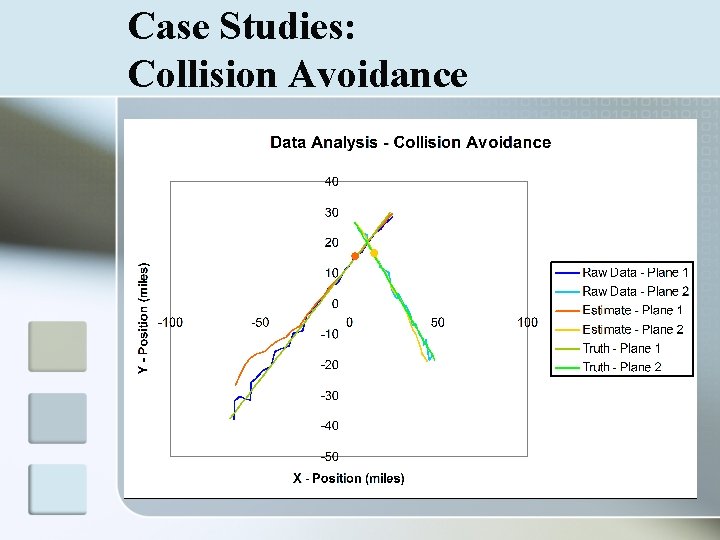
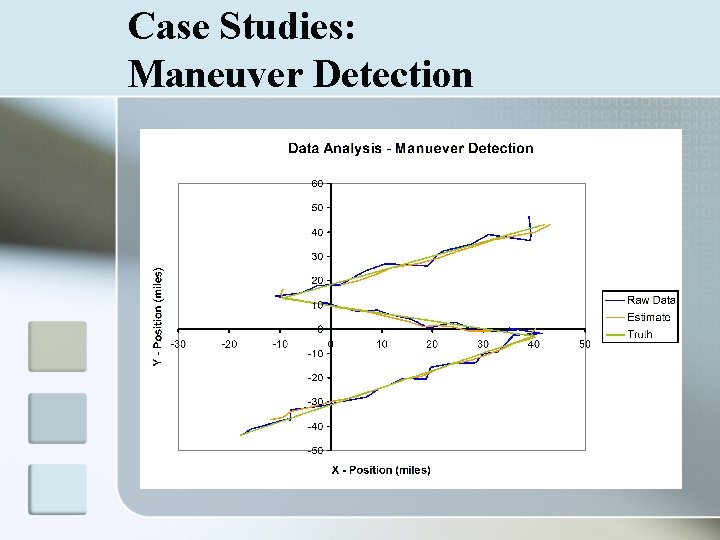
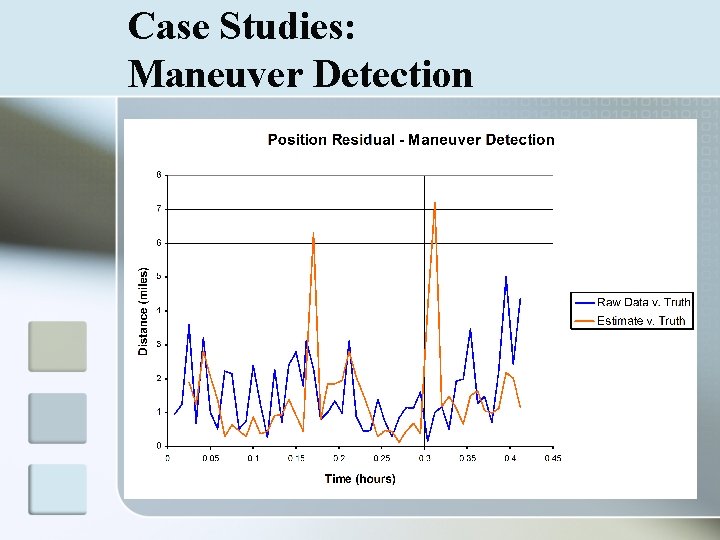
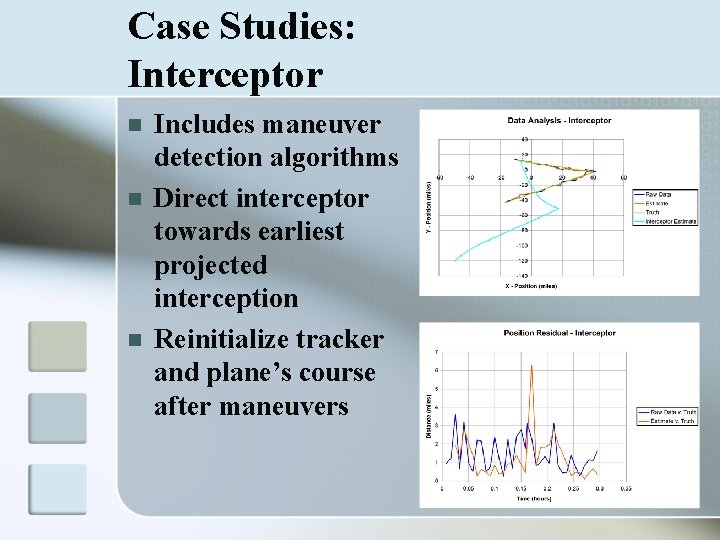
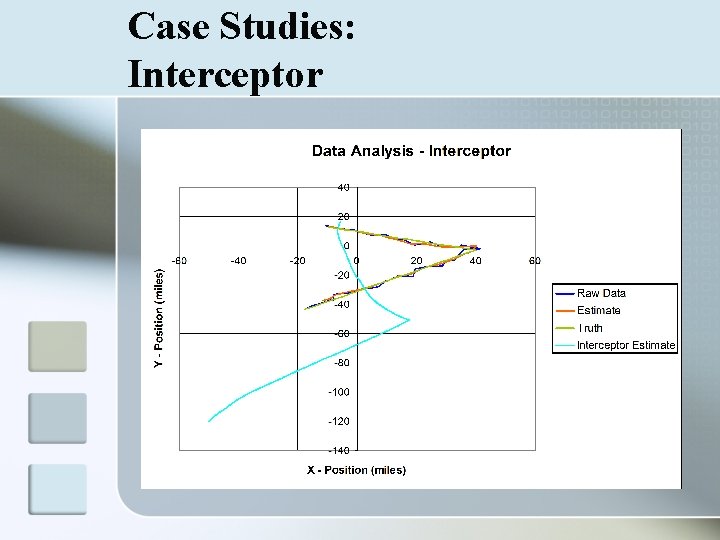
Case Studies: How to Read Graphs n Data Analysis n n n Comparison of raw data, estimated state, and truth Filter takes noisy data and projects a path close to the truth Position Residual n n Comparison of mean squared error Estimate v. Truth should decrease as filter gains accuracy relative to the Raw Data v. Truth

Case Studies: Basic Filter

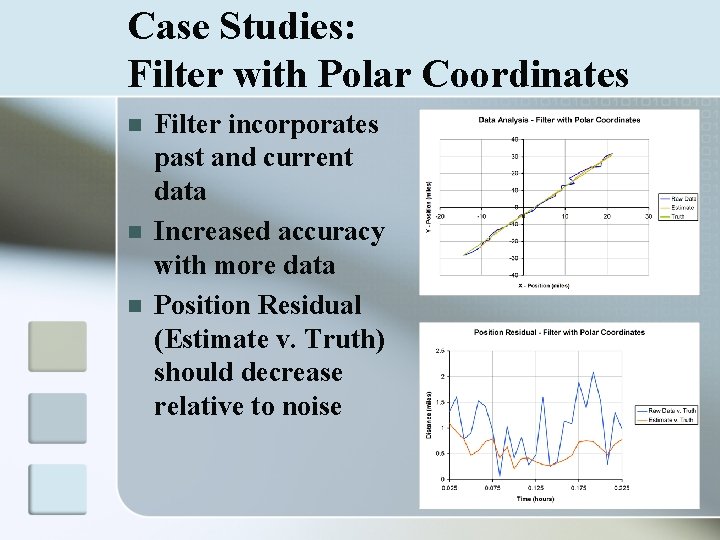
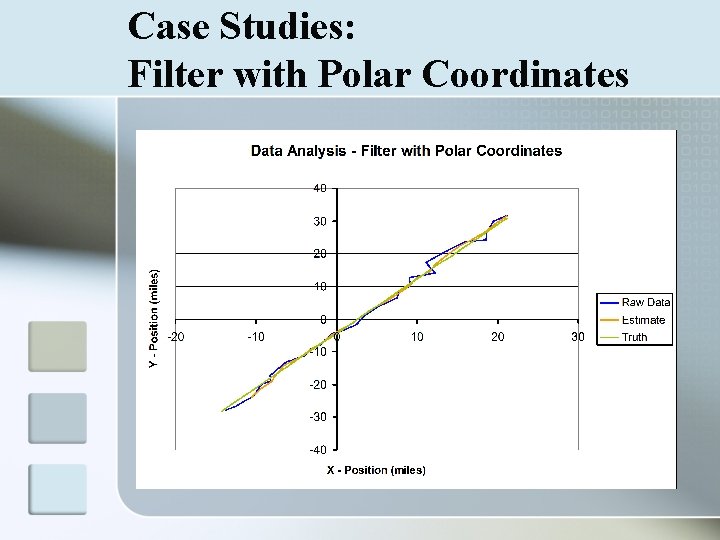
Case Studies: Filter with Polar Coordinates Data inputted in range and bearing n Challenges n Transformation of measurement data from Polar to Cartesian coordinates n Error ellipse based on accuracy of range and bearing n σθ σr

Case Studies: Filter with Polar Coordinates n n n Filter incorporates past and current data Increased accuracy with more data Position Residual (Estimate v. Truth) should decrease relative to noise

Case Studies: Filter with Polar Coordinates

Case Studies: Multiple Targets n n n Code rewrite necessary Object-oriented rather than structured programming Handles each target individually and allows the same steps to be used for each target

Case Studies: Multiple Targets

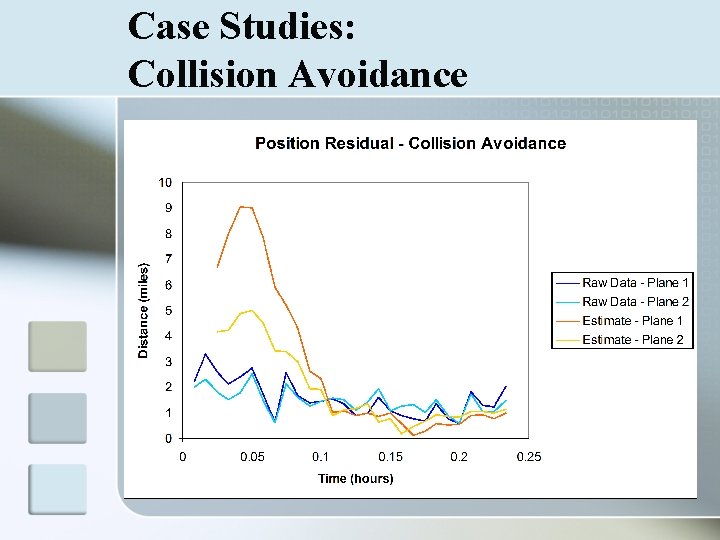
Case Studies: Collision Avoidance n n n Use data on multiple targets Predict collisions based on probable courses Alert target aircraft if within a certain range

Case Studies: Collision Avoidance

Case Studies: Maneuver Detection n Comparison of projected path and measured data When target deviates from projected course, reinitialize tracking Additional coding necessary

Case Studies: Maneuver Detection

Case Studies: Interceptor n n n Includes maneuver detection algorithms Direct interceptor towards earliest projected interception Reinitialize tracker and plane’s course after maneuvers

Case Studies: Interceptor

Conclusion Visual Basic. NET successfully handled the Kalman equations n Kalman Filter successfully reduced noise in all scenarios n Position Residual graphs confirms that the filter gains accuracy over time n Basic Filter proved expandable and advanced features were successfully incorporated in later scenarios n

Thank You

References n n n [IEEE] Institute of Electrical and Electronics Engineers. 2003 Jan 23. Rudolf E. Kalman, 1930 -. IEEE History Center. <http: //www. ieee. org/web/aboutus/history_center/biography/k alman. html> Accessed 2006 Aug 3. Department of Computer Science at University of North Carolina. 2001 Jan 31. Rudolph Emil Kalman. <http: //www. cs. unc. edu/~welch/kalman. Biblio. html> Accessed 2006 Aug 3. Blackman, Samuel S. 1986. Multiple-Target Tracking with Radar Applications. Artech House, Inc. Norwood, MA. Bishop G, Welch G. 2006. An Introduction to the Kalman Filter. <http: //www. cs. unc. edu/~welch/media/pdf/kalman_intro. pdf>. Accessed 2006 Aug 3. Anas SA. 2003 Jan 18. Matrix operations library. NET.