Principles of Programming Languages Slides by Gil Einziger

Principles of Programming Languages Slides by Gil Einziger Based on slides by Dana Fisman Based on lectures notes by Michael Elhadad Incorporating comments from Mira Balaban www. cs. bgu. ac. il/~ppl 202

Administrative - Online course - No midterm - Homework assignments (in pairs) - Uncertainty if there is an exam (Coronavirus and everything).

What is a Programming Paradigm? A paradigm is a way of thinking A programming paradigm is a way of programming it recommends preferred practices o it discourages (or makes impossible) risky practices o A programming paradigm influences o o o 3 code readability program performance ability to reason about the program (is it correct? ) reusability of the program fast development etc.

Programming Paradigms There are multiple programming paradigms, among which: o Imperative Control flow is an explicit sequence of commands o Declarative States the result you want, not how to get it o Structured o Procedural goto Programs have clean, goto-free, nested control structure Imperative programs organized around hierarchies of nested procedural calls o 4 …

Programming Paradigms o … o Functional f(g(x)) Computation proceeds by (nested) function calls that avoid any global state mutation and through the definition of function composition o Object-Oriented Computation is effected by sending messages to objects; objects encapsulate state and behavior o Event-Driven Control flow is determined by asynchronous actions in reaction to events o Bn B 1, …, H: - 5 Logic (Rule-based) Programmer specifies a set of facts and rules, and an engine infers the answers to questions

Imperative Example Control flow is an explicit sequence of commands. 10 INPUT "What is your name: "; U$ 20 PRINT "Hello "; U$ 30 INPUT "How many stars do you want: "; N 40 S$ = "" 50 FOR I = 1 TO N 60 S$ = S$ + "*" 70 NEXT I 80 PRINT S$ 90 INPUT "Do you want more stars? "; A$ 100 IF LEN(A$) = 0 THEN GOTO 90 110 A$ = LEFT$(A$, 1) 120 IF A$ = "Y" OR A$ = "y" THEN GOTO 30 130 PRINT "Goodbye "; U$ 140 END 16/ 110

Declarative Example …state the result you want, not how to get it. SELECT T 1. country_name FROM countries as T 1 JOIN continents AS T 2 ON T 1. continent = T 2. cont_id JOIN car_makers as T 3 ON T 1. country_id = T 3. country WHERE T 2. continent = 'Europe' GROUP BY T 1. country_name HAVING COUNT(*) >= 3

Structural Example Programs have clean, goto-free, nested control structures - arose in reaction to “goto hell” spaghetti code.

Object-oriented Example Computation is effected by sending messages to objects; objects encapsulate state and exhibit behavior. public class Person { public Person(String name, int age) { this. name = name; this. age = age; } public void say. Hello() { System. out. println("Hello, my name is " + name); } }

Event-driven Example Control flow is determined by asynchronous actions in reaction to events. document. add. Event. Listener("click", e => { console. log(`I was clicked at (${e. x}, ${e. y})`); });

Logic Programming Example Programmer specifies a set of facts and rules, and an engine infers the answers to questions. male(ben). female(dor). teacher(ben, ppl). teacher(dor, ppl). ? - teacher(X, ppl), female(X). X = dor.

Classifications of Languages Objected Oriented: C++, Java Functional: Haskel, ML, Scheme Many languages do not follow a particular paradigm Some Languages are multi-paradigm: Javascript, Python 1

What does a paradigm determines? Dimensions of variability across programming paradigms o o o o 1 Control flow Code organization Performance Coupling and reuse Testing and verification Syntax and readability Domain

Why should we learn this? Understanding these principles of programming languages will help us o o o 1 learn new languages compare existing languages choose the right language for a given task choose the right way to implement a given task build our own language when needed.

Functional Programming abbreviated FP 8

Functional Programming Expressions & Values Mostly characterized by the lack of state during computation o A computation is not a sequence of states created by commands/ statements o Rather it is a sequence of expressions that result from the evaluation of sub-expressions (define sum-even-squares (foldl + 0 (filter even? (map sqr '(1 2 3 4 5))))) In most IP computation will be preformed by intermediate states 16 In FP computation is a sequence of evaluations of sub-expressions

Functional Programming Example 3 +( i f a>10 then (2 * 3) e l s e (4 * 5 ) ) ; 3 + ( i f a>10 then (2 * 3) e l s e (4 * 5)); / / Computation proceeds i n s t e p s : / / step 1 - Evaluation: (2 * 3) ==>6 / / step 2 - Substitution: ==>3 +( i f a>10 then 6 e l s e / / step 3 - Evaluation: (4 * 5) ==>20 / / step 4 - Substitution: ==>3 +( i f a>10 then 6 e l s e / / step 5 - Substitution o f a : ==>3 +( i f 8>10 then 6 e l s e + / / step 6 - Evaluation: (8>10) ==>f a l s e / / step 7 - Substitution: ==>3 +( i f f a l s e then 6 e l s e +20) / / step 8 - Evaluation: i f f a l s e then 6 e l s e +20 ==>20 / / step 9 - Substitution: ==>3 +20 / / step 10 - Evaluation: 3 +20 ==>23 / / end: there are no more sub-expression t o evaluate ==>23 / / the value i s returned 17 Expressions & Values + (4 * 5)) + 20)

Functional Programming o Computations o In o The 18 in FP have no side effects the previous examples, we didn’t ask the program to print a result o Instead o No No Side. Effects we evaluated an expression (which was displayed at the end) only result of a functional computation is the computed value additional changes can take place during computation o If side-effects are required (opening files, printing, etc. ) they are usually deferred to the end. o FP does not support variable assignments or state mutations

Functional Programming Imperative Programming In IP commands/statements are executed, and through their effect, state is modified (mutated). 19 No Side. Effects Functional Programming vs. In FP expressions are evaluated and become values

Functional Programming Higher Order Functions FP requires function to be first class citizens (higher order function) This means functions are treated like any other value: ◦They can be passed as arguments ◦Functions can be returned as a result Functions can be anonymous (have no name) 20

Functional Programming in a nutshell By the end of the lesson we will see Characteristics of FP ◦ Functions and values (rather than states and statements) ◦ No side effects ◦ Higher order functions Advantages ◦Verification ◦Parallelism ◦Abstraction 21

Using Javascript to illustrate FP Javascript and Typescript o. Javascript o. The is a multi-paradigm language, it supports OOP and FP primitives of the language sometimes contradict good practices recommended by FP ◦ e. g. they allow easy mutations of variables and arrays ◦ but we will learn to avoid these o. Javascript is used extensively for front-end user interfaces in web and mobile applications o. Recent o. We frameworks such as Angular 2 and React rely extensively on FP will use Typescript (= version ES 7 of Javascript = Ecma. Script 2016) 22

From Imperative to Procedural We are asked to write a program to display a number value square console. log(0 ==> * 0); 0 The basic tool we used is a command/statement 23

From Imperative to Procedural We are now asked to to display a square of a range of integer values from 0 to 4 console. log(0 console. log(1 console. log(2 console. log(3 console. log(4 * * * 0) 1) 2) 3) 4) ==> 0 1 4 9 16 The basic tool we used is a sequence of commands This kind of program is referred to as “level 0” program 24

Structured Programming Structured programming starts with a critique of this “level 0” program o Code repetition o Cannot be easily adapted to different values of parameters o The nature of the task is not reflected in the program console. log(0 * 0) console. log(1 * 1) console. log(2 * 2) console. log(3 * 3) console. log(4 * 4) Structured programming improves on this by introducing the following program contracts: o Variables to capture parameters o Use arrays to separate data and task execution o Use loop control flow structure to reflect the nature of the task let for 25 } numbers = [ 0 , 1 , 2 , 3 , 4 ] ; ( l e t i = 0; i < numbers. length; i ++) console. log(numbers[i] * numbers[i]); { ==> 1 4 9 16 0

Structured Programming The programming constructs introduced are o For-loop o Array o Variables Now it is easy to change the code to apply it to different parameters l e t numbers = [ 8 , 9 , 10, 11, 12]; f o r ( l e t i = 0; i < numbers. length; i ++) { console. log(numbers[i] * numbers[i]); } 26 ==> 64 81 100 121 144

Procedural Programming Procedural programming starts with a critique of this structural programming o We have to duplicate the code for each run with different parameters o The coupling between the code and the parameters is accidental - Which variables correspond to parameters? - Can other parts of the code change these variables? Procedural programming improves on this by introducing o Procedures - With well defined interface of input parameters, output parameters, and expected behavior o Local variables - Variables that are defined only in the scope of the procedure 27

Procedural Programming function print. Squares(numbers) { f o r ( l e t i = 0 ; i < numbers. length; i++) { console. log(numbers[i] * numbers[i]); } } print. Squares([0, print. Squares([8, 1, 2, 3, 4]); 9 , 10, 11, 1 2 ] ) ; ==> 0 1 4 9 16 64 81 100 121 144 The program constructs introduced are 28 o function and o let which defines local variables for a block of statements

Procedural Programming Procedures (also called functions) have a well defined interface o Name o Input variables o Return value Why is naming a function important? o It provides an abstraction ◦ the name replaces a complex sequence of commands ◦ it can be re-used without understanding its details, only its interface 29

Procedural Programming Suppose we are now asked to print the cubes instead of the squares? o We can define a new function computing what we want to do for each element o And modify print. Squares() to use that function / / We use a l i b r a r y function Math. pow function cube(number) { return Math. pow(number, 3); } function print. Cubes(numbers) { f o r ( l e t i = 0; i < numbers. length; console. log(cube(numbers[i])); } } print. Cubes([0, 1, 2, 3, 4 ] ) ; print. Cubes([8, 9 , 10, 11, 1 2 ] ) ; 30 i ++) { ==> 0 1 8 27 64 512 729 1000 1331 1728

Procedural Programming Abstraction barriers: print. Cubes() > cube() > Math. pow() print. Squares() > squares() To support such barriers some programming languages introduce the concepts such as modules or packages 31

Is the program correct? We would like to prove that the procedure is correct according to its specification. Functions that just print (such as print. Cubes) are hard to verify. To cope with this we will refactor the program in 2 stages o Data transformation - Receives and input parameter - Returns a value o Data output - prints the transformed values 32

Is the program correct? function cubes(numbers) { f o r ( l e t i = 0; i <numbers. length; numbers[i] = cube(numbers[i]); } } function print. Array(a) { f o r ( l e t i = 0; i < a. length; console. log(a[i]); } } function print. Cubes 2(numbers) cubes(numbers); print. Array(numbers); } / / Test print. Cubes 2([0, 1, 2, 3, 4] ) ; 33 i ++) { { { ==> 0 1 8 27 64

Writing a test module / / The assert l i b r a r y i s used to perform t e s t s const assert =r e q u i r e ( ‘ a s s e r t ' ) ; function test. Cubes() { / / Empty l i s t l e t numbers =[ ] ; cubes(numbers); assert. ok(numbers. length ==0 ) ; / / Invariant cubes are not modified numbers =[ 0 , 1 ] ; cubes(numbers); assert. deep. Equal([0, 1], numbers, "invariant cubes"); / / Regular numbers =[ 2 ] ; cubes(numbers); assert. deep. Equal(numbers, [ 8 ] , "cube(2) === 8”) ; return " a l l ok"; } 27 test. Cubes(); ==> 'all ok'

Procedural Paradigm - Pros We obtained a nice version of our program: o Code is organized in layers of abstraction [print. Cubes > [print. Arrays, cubes] > power] o Structured loops (for) are used to iterate over arrays, in a manner that reflects the task o It can be tested These good features were enabled by the facilities of the programming language we use: o It is easy to define arrays, name them, initialize them, pass them, access their elements o It is easy to define functions o Functions can invoke other functions (given the interfaces is known) o It is easy to test functionalities using facilities like assert. The programming language encouraged us to organize our program in a good manner. 35

Procedural Paradigm - Cons When we scale to larger and more interesting programs, we face new types of problems o The flow of variables across functions must be explained: -are parameters passed by value (in parameters) or by reference (inout parameters)? -How returned values are shared between the caller and the called function? o The responsibilities around data structures must be clarified: -Which functions can only read data, and which functions can read and modify data? -When is data allocated and freed? We will return to these issues when we discuss variables and scopes. These aspects have motivated the development of the Object Oriented Paradigm. 36

Procedural Paradigm - Cons For now, we will focus on the following issues of the procedural paradigm o. Procedural programming encourages shared state with mutation which makes concurrency difficult. o. Procedural programming commits early to a step by step way to implement operations which prevents performance optimizations. o. Procedural programming makes it difficult to create functional abstractions that are highly reusable. o. Procedural programming makes it difficult to reason about code because of shared state and mutations. We will see how these issues are addressed by FP. 37

The Concurrency issue in procedural programming Suppose we run the procedure cube in two concurrent threads (using an executor as we learned in SPL) on the same array numbers. function cubes(numbers) { f o r ( l e t i =0 ; i <numbers. length; i++) { numbers[i] =cube(numbers[i]); } } If the 2 threads are interleaved in an unfortunate sequence of events - the following scenario can occur: l e t n 89 =[ 8 , 9 ] ; Thread 1 / / In Thread 1 : numbers[1]=64 cubes(n 89); numbers[2]=81 numbers[1]=64 Thread 2 numbers[2]=6561 / / In Thread 2 : cubes(n 89); 38 Many other unexpected values can occur

The Concurrency issue in procedural programming Cause of problem: uncontrolled access to shared variables How can one solve this lack of concurrency safety? Solution immutable data structures ort p p u to s d r ral Ha u d e oc in pr mming tion ra u l g o o s r p FP! fe the y b ted lves also unsadue to adop so tation u comp n in the s tio hread muta t f o ce absen enforce mutualexclusion using locks in e c i o h lt c defau ural d proce mming a progr ems l b o r to p s d a le ess n e v i l of of y t i l i b i (poss ks, oc deadl ions, etc. ) at starv

Declarative vs. Procedural How do we iterate over array elements? function cubes(numbers) { f o r ( l e t i = 0; i <numbers. length; numbers[i] = cube(numbers[i]); } } Using a counter variable i Can we also iterate backwards? Does it matter? 40 i ++) {

Declarative vs. Procedural In FP we prefer to abstract away the array is traversed We want a simple way to prescribe: “apply a certain operation on all elements of an array”. array. map(f) This abstract operation is called map. x 2 x 3 x 4 x 5 f cubes 3([0, 1, 2]); f(x 1) f(x 2) f(x 3) f(x 4) f(x 5) ==>[ 0 , 1 , 8 ] 41 x 1 function cubes 3(numbers) { return numbers. map( cube); } f f

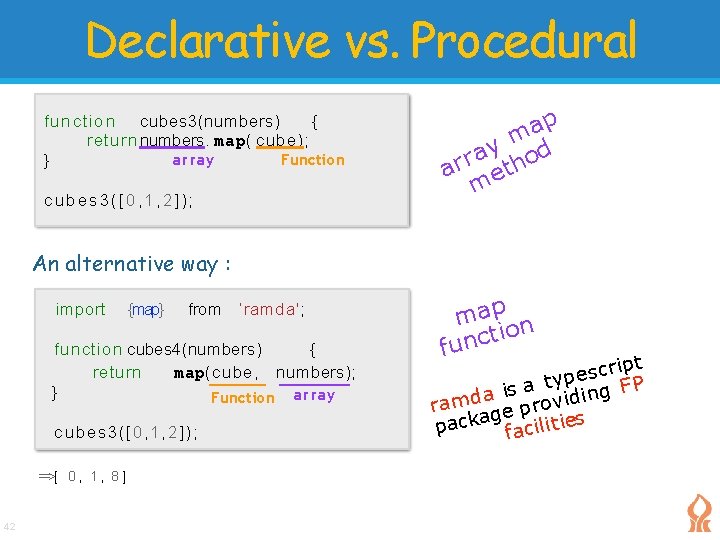
Declarative vs. Procedural function cubes 3(numbers) { return numbers. map( cube); array Function } cubes 3([0, 1, 2]); p a m y a hod r r t a e m An alternative way : import {map} from ‘ramda'; function cubes 4(numbers) { return map(cube, numbers); } Function array cubes 3([0, 1, 2]); ==>[ 0 , 1 , 8 ] 42 map n io t c n fu ipt r c s e typ g F P a s i a in ramd ge provid packa facilit ies

Functional Abstractions Suppose now we are required to print the exponential value of all elements in a list of numbers. exponent } function cubes(numbers) { … Math. exp(…) function print. Array(a) { … } print. Exponent function print. Cubes 2(numbers) { exponent cubes(numbers); print. Array(numbers); } 43 console. log( map(cube, numbers) ) console. log( map(Math. e x p , numbers) ) n is o i t c tra s b a s to a k n This a th pass d e l b ena bility to s a t he a nction a r fu te e m a par

How would you name this function? 44 Receives: Returns: x x*x Receives: Returns: a = a 1, a 2, …, an (a 1 + a 2 + … + an)*(1/n) Receives: Returns: x 327(x*x) + 53 Should we always insist to give a function a name?

Anonymous functions In FP it is possible to define a function without giving it a name. In which case it is called an anonymous function or a lambda function The syntax in Javascript is: ( <parameters> ) => <expression> Examples: ( x ) => x*x (x, y) => x*x + 2*x*y + y*y Example of use: map(x => x * x , 45 [0, 1, 2, 3]) ==>[ 0 , 1 , 4 , 9 ]

Anonymous functions Another possible syntax in Javascript is: function (<parameters>) {<body>} Example: function ( x ) {return x * x; } Example of use: map (function ==>[ 0 , 1 , 4 , 9 ] 46 ( x ) {return x * x; }, [0, 1, 2, 3])

More functional abstractions Suppose we want to apply a function to a list of numbers, and then keep only the values that are even function is. Even(n) { return n % 2 ==0 ; } function map. And. Keep. Even(f, a ) { l e t f a =a. map(f); l e t res =[ ] ; f o r ( l e t i =0 ; i <f a. l e n g t h ; i++) { i f is. Even(fa[i]) { res =r e s. c o n c a t ( f a [ i ] ) ; }} return res; } map. And. Keep. Even((x)=>x*x, [ 0 , 1 , 2 , 3 , 4 , 5 ] ) ==>[ 0 , 4 , 16 ] 47

More functional abstractions - Filter The pattern of iterating over an array and keeping only elements that satisfy a certain condition is extremely useful. FP languages include a function to make this operation easy to use - most often called filter(p? , a) [1, 2, 3, 4]. filter(is. Even) ==>[ 2 , 4 ] x 1 ==>[ 2 , 4 ] 48 x 3 x 4 x 5 p? (x 1) p? (x 2) p? (x 3) p? (x 4) p? (x 5) Yes filter(is. Even, [1, 2, 3, 4]) x 2 Yes No Yes x 1 x 2 x 4 No

More functional abstractions Back to our example function map. And. Keep. Even(f, a ) { l e t f a =a. map(f); return f a. f i l t e r ( i s E v e n ) ; } More concisely function map. And. Keep. Even(f, a ) { return a. map(f). filter(is. Even); } More abstractly Usage 42 function map. And. Filter(f, pred, a ) { return a. map(f). filter(pred); } map. And. Filter(cube, is. Even, [ 0 , 1 , 2 , 3 , 4 ] ) ==>[ 0 , 8 , 64 ]

More functional abstractions We can simply chain map and filter, without a pre-defined encapsulating function [0, 1, 2, 3, 4, 5]. map((x)=>x*x). filter((x)=>x%2==0) ==>[ 0 , 4 , 16 ] Or using the functions filter and map of ramada package (rather than the filter and map functions of array) import * as Rfrom 'ramda'; R. f i l t e r ( i s E v e n , R. map(cube, [ 0 , 1 , 2 , 3 , 4 , 5 ] ) ) ==>[ 0 , 8 , 64 ] 50

More functional abstractions - compose Such composition is also a very general pattern, that we would like to be able do easily compose ( f , g) f(g(x)) l e t even. Cubes =R. compose(R. filter(is. Even), R. map(cube)) even. Cubes([0, 1, 2, 3, 4]) ==>[ 0 , 8 , 64 ] 51

important aspects of FP o Functions can receive functions as parameters - including anonymous functions - for example: map, filter, compose o Functions can return functions as computed value -for example compose returns a new function as a computed value -the returned function might depend on inputs, and thus can only be computed at runtime 52

Reasoning about the code Is my program correct? Will it behave correctly on all inputs? How much memory its computation takes? How much steps its computation involves? Is it equivalent to this simpler/otherwise possibly better program? 53

Reasoning about the code For instance, we might ask whether the following two programs are equivalent? R. compose(R. filter(is. Even), R. map(cube)) R. compose(R. map(cube), R. f i l t e r ( i s E v e n ) ) lly a i t n Pote ms less r prefo ations oper Suppose they are equivalent, should we prefer one over the other? 54

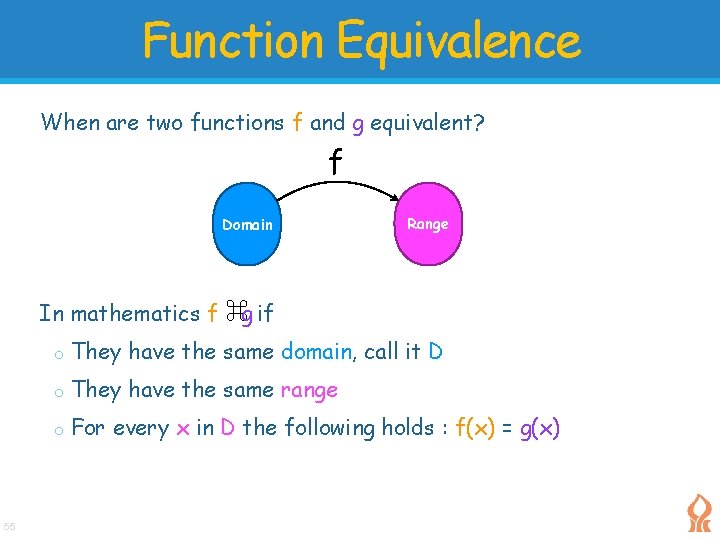
Function Equivalence When are two functions f and g equivalent? f Domain Range In mathematics f ⌘g if 55 o They have the same domain, call it D o They have the same range o For every x in D the following holds : f(x) = g(x)

Function Equivalence In FP a pure function has no side effects. Basically, the same definition applies. But we have to take into account, that oa computation can throw an exception oa computation may not terminate Thus, we define that f and g are equivalent if 56 o Whenever f(x) is evaluated to a value, then g(x) is evaluated to the same value o If f(x) throws and exception, so does g(x) o If f(x) does not terminate, so does g(x)

Are they equivalent? How do we check equivalence? We have to go over all values x of the domain D There could be infinitely many such values (e. g. if the domain is integers) To prove that a program is correct, we have to use the semantics of the programming language in which it is written. The semantics of a programming language is the set of definitions providing to each operator of the language, its meaning. 57

Proving correctness The semantics of pure functional programming language is much easier to develop than that of procedural programs with side effects. This is because it can be based on an inductive process of evaluation of expressions which only focuses on the structure of the input expression. We will develop such tools in the course, relying extensively on types and the technique of structural induction. The property of functional programs which makes this process easy is called referential transparency 58

Referential Transparency Referential transparency means that o the value of a program (called an expression in FP) depends only on its sub-expressions, and that if you substitute a sub-expression in an expression by another expression that is equivalent, then the resulting expression is equivalent to the original. o Some consequences of referential transparency are that o if one evaluates an expression twice, one obtains the same result o. The relative order in which one evaluates (non-overlapping) subexpressions of a program makes no difference to the value of the program. o. This property enables optimization methods such as parallel evaluation of sub-expressions to speed up code. 59

Proving Function Equivalence We want to check if the following two expressions are equivalent? f =R. compose(R. filter(is. Even), R. map(cube)) g =R. compose(R. map(cube), R. f i l t e r ( i s E v e n ) ) First we need to establish what the domain is. What is its type? It is a finite array of integer values a = [ a 1 , . . . , a n ] We want to check that f ( a ) 60 = g ( a ) for all arrays a

Proving Function Equivalence We develop f and g following their definitions f ( a ) =f i l t e r ( i s E v e n , map(cube, a ) ) =f i l t e r ( i s E v e n , [ c u b e ( a 1 ) , . . . , c u b e ( a n ) ] ) g ( a ) =map(cube, f i l t e r ( i s E v e n , a ) ) =map(cube, f i l t e r ( i s E v e n , [ a 1 , . . . , a n ] ) ) To continue we need to apply the definition of filter(pred, [a 1 , . . . , an ]) [ a i 1, …, a i k] = ∣ 1 ≤ i 1 < i 2 < … < ik n ≤, ∀ j ∈ {i 1 , …, i k }, pred(a j ) ∀ j ∉ {i 1 , …, i k }, pred( a j ) 61 i s true and is false.

Proving Function Equivalence We obtain f(a) =f i l t e r ( i s E v e n , map(cube, a ) ) =f i l t e r ( i s E v e n , [cube(a 1 ), …, cube(a n )]) =[cube(a i 1 ) , … , cube(a i k ) ] ∀ ∣ j ∈{i 1 , …, i k }, is. Even(cube(a j )) g ( a ) =map(cube, f i l t e r ( i s E v e n , a ) ) =map(cube, f i l t e r ( i s E v e n , [a 1 , …, a n ])) =map(cube, [a j 1 , …, a j m ] ∀ ∣ j ∈{j 1 , …, j m }, i s E v e n ( a j ) ) =[cube(a j 1 ) , … , cube(a j m )] ∀ ∣ j ∈{j 1 , …, j m }, i s E v e n ( a j ) To prove the equivalence, we must then prove that ∀i∈N, i s E v e n ( i ) =is. Even(cube(i)) Proof is enabled due to o application of reduction steps o where each step follows the formal semantics of the reduced sub-expression o in particular that of filter and map