Principles of Programming Languages Practice session 7 The

Principles of Programming Languages Practice session 7

The Sequence Interface . לכל האיברים 1 למשל להוסיף , רוצים לבצע פעולה כלשהי על אוסף : Java- ב for (int i = 0; i < list. Len; i++) { our. List[i] = our. List[i] + 1; } : Scheme- ב Signature: func (ls) Type: [LIST(Number)->LIST(Number)] (define func (lambda (ls) (if (null? ls) ls (cons (+ 1 (car ls)) (func (cdr ls)))))) : Sequence של הממשק map ע"י שימוש בפונקציה > (define func (lambda (ls) (map (lambda (x) (+ 1 x)) ls))) � �

The Sequence Interface שמקבלת dists_k רוצים לממש את הפרוצדורה : 1 שאלה , (x, y) רשימה של זוגות מספרים המייצגים קואורדינטות ומחזירה את המרחק מהראשית של כל הנקודות המקיימות . x=k Signature: dists_k (ls k) Type: [LIST(Number*Number) ->LIST(Number)] Examples: (dists_k (list (cons 3 4) (cons 3 7) (cons 15 12) (cons 3 12)) 3) => '(5 7. 615773105863909 12. 36931687685298) : פונקציית העזר הנ"ל נתונה לנו > (define dist (lambda (x y) (sqrt (+ (sqr x) (sqr y)))))

Currying : 2 שאלה >(define dist (lambda (x y) (sqrt (+ (sqr x) (sqr y))))) > (define c_dist (lambda (x) (let ((xx (sqr x))) (lambda(y) (sqrt (+ (sqr y) xx)))))) : החדש dists_k מימוש > (define dists_k (lambda(ls k) (let ((dist_k (c_dist k))) (map (lambda (x) (dist_k (cdr x))) (filter (lambda (x) (= (car x) k)) ls)))))

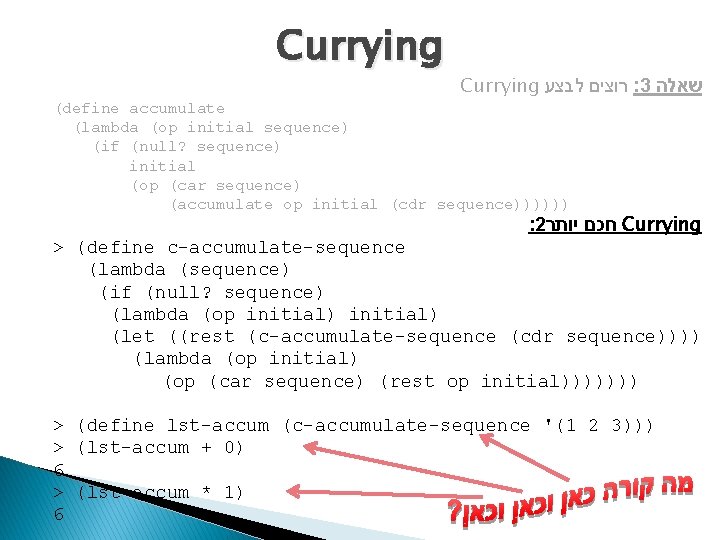
Currying : כפי שראיתם בהרצאה accumulate ניזכר בפונקציית : 3 שאלה Signature: accumulate(op initial sequence) Purpose: Accumulate by ’op’ all sequence elements, starting (ending) with ’initial’ Type: [[T 1*T 2 -> T 2]*T 2*LIST(T 1) -> T 2] (define accumulate (lambda (op initial sequence) (if (null? sequence) initial (op (car sequence) (accumulate op initial (cdr sequence))))))

Currying רוצים לבצע : 3 שאלה (define accumulate (lambda (op initial sequence) (if (null? sequence) initial (op (car sequence) (accumulate op initial (cdr sequence)))))) : נאיבי Currying (define c-accumulate-naive (lambda (op initial) (lambda (sequence) (if (null? sequence) initial (op (car sequence) ((c-accumulate-naive op initial) (cdr sequence)))))))

Currying : נאיבי Currying (define c-accumulate-naive (lambda (op initial) (lambda (sequence) (if (null? sequence) initial (op (car sequence) ((c-accumulate-naive op initial) (cdr sequence))))))) > (define add-accum (c-accumulate-naive + 0)) > (add-accum '(1 2 3)) > (add-accum '(4 5 6))

Currying רוצים לבצע : 3 שאלה (define accumulate (lambda (op initial sequence) (if (null? sequence) initial (op (car sequence) (accumulate op initial (cdr sequence)))))) : חכם יותר Currying > (define c-accumulate-op-initial (lambda (op initial) (letrec ((iter (lambda (sequence) (if (null? sequence) initial (op (car sequence) (iter (cdr sequence))))))) iter))) > (define add-accum (c-accumulate-op-initial + 0)) > (add-accum '(1 2 3)) > (add-accum '(4 5 6))

Currying רוצים לבצע : 3 שאלה (define accumulate (lambda (op initial sequence) (if (null? sequence) initial (op (car sequence) (accumulate op initial (cdr sequence)))))) : 2 חכם יותר Currying > (define c-accumulate-sequence (lambda (sequence) (if (null? sequence) (lambda (op initial) (let ((rest (c-accumulate-sequence (cdr sequence)))) (lambda (op initial) (op (car sequence) (rest op initial))))))) > (define lst-accum (c-accumulate-sequence '(1 2 3))) > (lst-accum + 0) 6 > (lst-accum * 1) 6

The Sequence Inteface המקבלת flatmap רוצים לממש את הפרוצדורה : 4 שאלה מפעילה על איברי הרשימה את , רשימה ופרוצדורה . הפרוצדורה ולאחר מכן משטחת את הרשימה � Signature: flatmap (proc seq) Type: [ [T 1 ->T 2] * List(T 1) -> List(T 3)] Purpose: ◦ Applies a function on every element of the given list, resulting in a new nested list ◦ Flattens the nested list (not recursively). : דוגמת הרצה > (define ls (list 1 2 3) (list 4 6 7) (list 8 9))) > (flatmap cdr ls) => '(2 3 6 7 9) > (flatmap (lambda (lst)(filter odd? lst)) ls) => '(1 3 7 9)

The Sequence Inteface : 4 שאלה � Signature: flatmap (proc seq) Type: [ [T 1 ->T 2] * List(T 1) -> List(T 2)] Purpose: ◦ Applies a function on every element of the given list, resulting in a new nested list ◦ Flattens the nested list (not recursively). (define flatmap (lambda (proc seq) (accumulate append (list) (map proc seq))))

Lazy Lists Signature: cons(head, tail) Type: [T * [Empty->Lazy. List] -> Lazy. List] Purpose: Value constructor for lazy lists : ממשק Signature: head(lzl) Type: [Lazy. List -> T] Purpose: Selector for the first item of lzl (a lazy list) Pre-condition: lzl is not empty Signature: tail(lzl) Type: [Lazy. List -> Lazy. List] Purpose: Selector for the tail (all but the first item) of lzl (a lazy list) Pre-condition: lzl is not empty Signature: nth(lzl, n) Type: [Lazy. List * Number -> T] Purpose: Gets the n-th item of lzl (a lazy list) Pre-condition: lzl length is at least n, n is a natural number Post-condition: result=lzl[n-1] Signature: take(lzl, n) Type: [Lazy. List * Number -> List] Purpose: Creates a List out of the first n items of lzl (a lazy list) Pre-condition: lzl length is at least n, n is a natural number Post-condition: result[i]=lzl[i] for any i in range 0: : n-1 �

Lazy Lists : כנ"ל lazy list רוצים לממש פונקציה שתיצור : 5 שאלה � Signature: integers-from (low) Purpose: Creates a lazy list containing all integers bigger than n-1 by their order Pre-condition: n is an integer > (define integers-from (lambda(n) (cons n (lambda () (integers-from (+ 1 n)))))) > (head (integers-from 5)) 5 > (head (tail (integers-from 5)))) 6

Lazy Lists . 7 BOOM רוצים לממש רשימה שתספור לפי חוקי : 6 שאלה � > (define gen_item (lambda (n) (cons (if (or (divided_by_7? n) (has_digit_7? n)) 'boom n) (lambda () (gen_item (+ n 1)))))) > (gen_item 1) '(1. #<procedure>) > (take (gen_item 1) 7) '(1 2 3 4 5 6 boom) ? (gen-item 1) מה הטיפוס של ? well-typed והאם הביטוי הוא � �

Lazy Lists רוצים לממש רשימה עצלה של המספרים הראשוניים ע"י : 7 שאלה . Sequence שימוש בממשק � >(define primes (cons 2 (lambda()(lz-lst-filter prime? (integers-from 3))))) >(define prime? (lambda (n) (letrec ((iter (lambda (lz) (cond ((> (sqr (head lz)) n) #t) ((divisible? n (head lz)) #f) (else (iter (tail lz))))) )) (iter (integers-from 2))) )) > (take primes 6) ’(2 3 5 7 11 13)

Lazy Lists רוצים לממש רשימה עצלה של המספרים הראשוניים ע"י : 7 שאלה . – אלגוריתם הנפה Sequence שימוש בממשק > (define sieve (lambda (lz) (cons (head lz) (lambda () (sieve (lz-lst-filter (lambda(x) (not (divisible? x (head lz)))) (tail lz))))) )) > (define primes 1 (sieve (integers-from 2))) �