Principles of Programming Languages Lecture 03 Theoretical Foundations

Principles of Programming Languages Lecture 03 Theoretical Foundations C SC 520 Principles of Programming Languages 1

Domains • Semantic model of a data type: semantic domain n Examples: Integer, Natural, Truth-Value • Domains D are more than a set of values n n Have an ``information ordering’’ on elements—a partial order-where x y means (informally): ``y is as least as well-defined as x’’ There is a ``least defined’’ element such that ( x) x which represents an undefined value of the data type u u n Or the value of a computation that fails to terminate ``bottom’’ Domains are complete: every monotone (non-decreasing) sequence in D has in D a least upper bound, i. e. , an element denoted such that and l is least element with this property u D sometimes called a ``complete partial order’’ or CPO C SC 520 Principles of Programming Languages 2

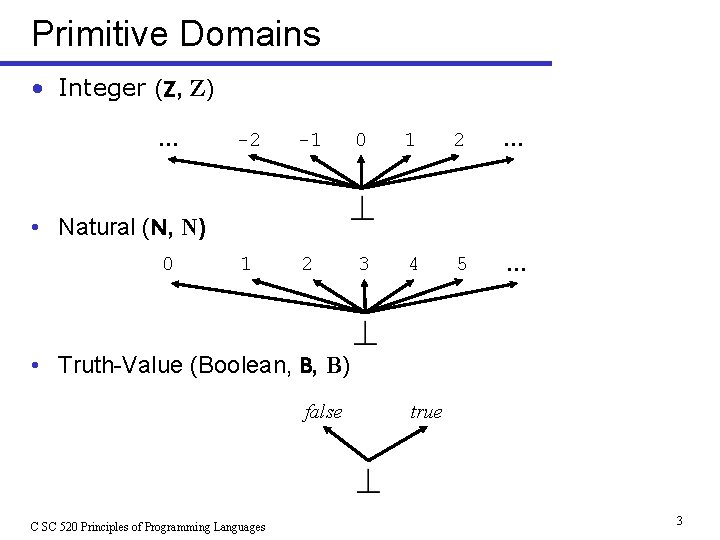
Primitive Domains • Integer (Z, Z) … -2 -1 0 1 2 … 1 2 3 4 5 … • Natural (N, N) 0 • Truth-Value (Boolean, B, B) false C SC 520 Principles of Programming Languages true 3

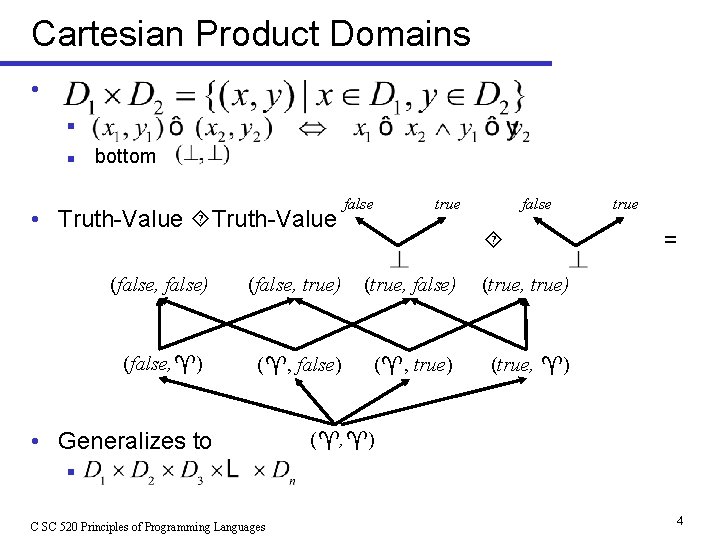
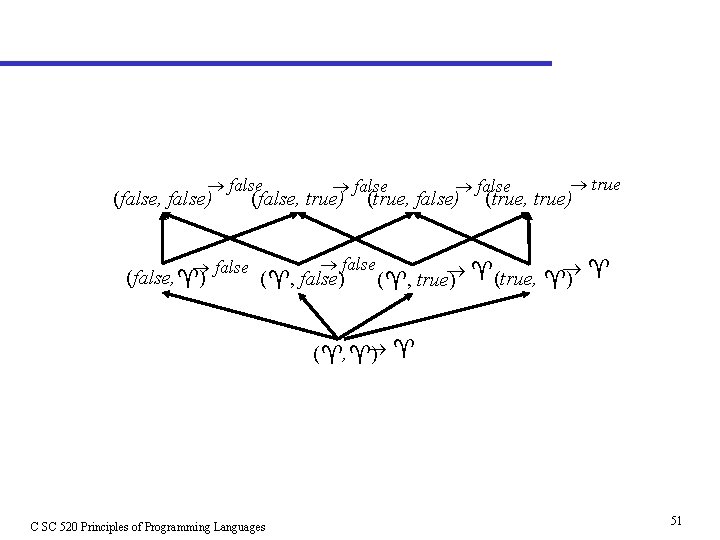
Cartesian Product Domains • n n bottom • Truth-Value false true false (false, false) (false, true) (true, false) (true, true) (false, ) ( , false) ( , true) (true, ) • Generalizes to true = ( , ) n C SC 520 Principles of Programming Languages 4

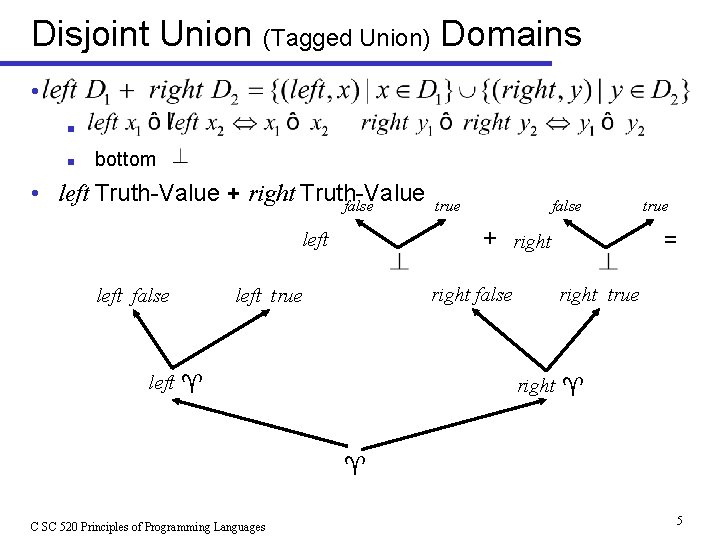
Disjoint Union (Tagged Union) Domains • n n bottom • left Truth-Value + right Truth-Value false + right left false true right false left true left true = right true right C SC 520 Principles of Programming Languages 5

Disjoint Union Domains (cont. ) • Convention: tags are also names for mappings (injections) —tagging operators n C SC 520 Principles of Programming Languages 6

Disjoint Union Domains (cont. ) • Example: union domains needed when data domains consist of different type elements (union types): imagine a very simple programming language in which the only things that can be named (denoted) are non-negative integer constants, or variables having such as values. n Dereferencing operation: u Constant values dereference directly to their values u Variables (locations) dereference to their contents in memory C SC 520 Principles of Programming Languages 7

Sequence Domains • Consist of homogenious tuples of lengths 0, 1, … over a common domain D n n Examples: n Concatenation operator n Empty tuple nil C SC 520 Principles of Programming Languages 8

Functions • A function f from source domain X to target domain Y is n A subset of X Y : f X Y (a relation) n Single-valued: n Source domain X n Target domain Y f: X Y • Domain of f : n If X = dom f then f is total ; otherwise partial • To define (specify) a function, need to give n Source X n Target Y n Signature n Mapping rule x f(x) C SC 520 Principles of Programming Languages 9

Functions (cont. ) • Example: n n Let R = Real. Not the same function as: Let N = Natural. Not the same as: - fun sq(n: int): int = n*n; val sq = fn : int -> int - sq(3); val it = 9 : int - sq(1. 5); std. In: 11. 1 -11. 8 Error: operator and operand don't agree [tycon mismatch] operator domain: int operand: real in expression: sq 1. 5 - fun sq 1(x: real): real = x*x; val sq 1 = fn : real -> real - sq 1(1. 5); val it = 2. 25 : real - sq 1(3); std. In: 16. 1 -16. 7 Error: operator and operand don't agree [literal] operator domain: real operand: int in expression: sq 1 3 C SC 520 Principles of Programming Languages - 10

Defining Functions • Two views of ``mapping’’ n Extension: view as a collection of facts n Comprehension: view as a rule of mapping u u n n Combinator form: -abstraction form: Typed -calculus In ML u = fn u . = u ( x • e) = (fn x => e) => C SC 520 Principles of Programming Languages - fun square(x) = x*x; val square = fn : int -> int - square(4); val it = 16 : int - val square = (fn y => y*y); val square = fn : int -> int - square(5); val it = 25 : int 11

Defining Functions (cont. ) • Examples of -notation defining functions • u u C SC 520 Principles of Programming Languages 12

Defining Functions (cont. ) - val double = (fn n => n+n); val double = fn : int -> int - val successor = (fn n => n+1); val successor = fn : int -> int - val twice = (fn f => (fn n => f(f(n)))); val twice = fn : ('a -> 'a) -> 'a - val twice = (fn f : int -> int => (fn n : int => f(f(n)))); val twice = fn : (int -> int) -> int - val td = twice(double); val td = fn : int -> int - td(3); val it = 12 : int - val ts = twice(successor); val ts = fn : int -> int - ts(3); val it = 5 : int C SC 520 Principles of Programming Languages 13

Defining Functions (cont. ) - fun double(n) = n+n; val double = fn : int -> int - fun successor(n) = n+1; val successor = fn : int -> int - fun twice(f)(n) = f(f(n)); val twice = fn : ('a -> 'a) -> 'a - fun twice(f : int -> int )(n : int) = f(f(n)); val twice = fn : (int -> int) -> int - fun td = twice(double); std. In: 39. 5 -39. 7 Error: can't find function arguments in clause - twice(double)(3); val it = 12 : int - twice(successor)(3); val it = 5 : int - fun compose(f)(g)(n) = f(g(n)); val compose = fn : ('a -> 'b) -> ('c -> 'a) -> 'c -> 'b - val csd = compose(successor)(double); val csd = fn : int -> int - csd(3); val it = 7 : int C SC 520 Principles of Programming Languages 14

Function Domains • Elements are functions from a domain to another • Domain of functions denoted • Not all functions—must be monotone: if n Idea: more info about argument more info about value • Ordering on domain • Bottom element of domain n “totally undefined’’ function • Technical requirement: functions must be continuous: C SC 520 Principles of Programming Languages 15

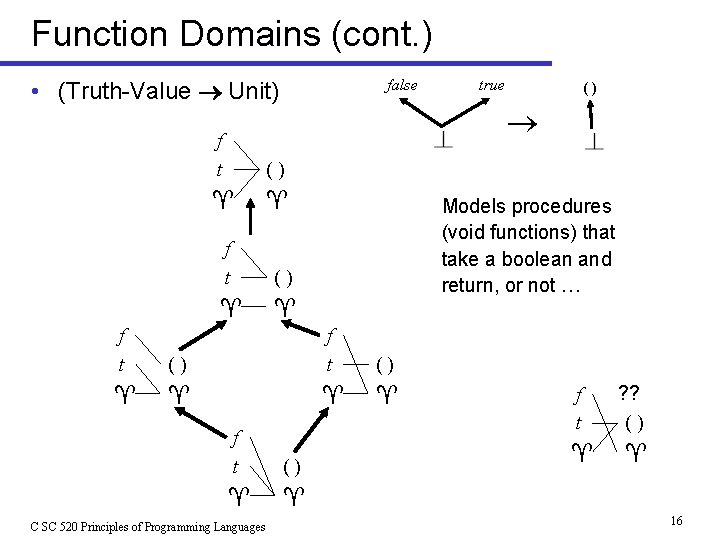
Function Domains (cont. ) • (Truth-Value Unit) f t () C SC 520 Principles of Programming Languages () Models procedures (void functions) that take a boolean and return, or not … f t true () f t false () f t ? ? () 16

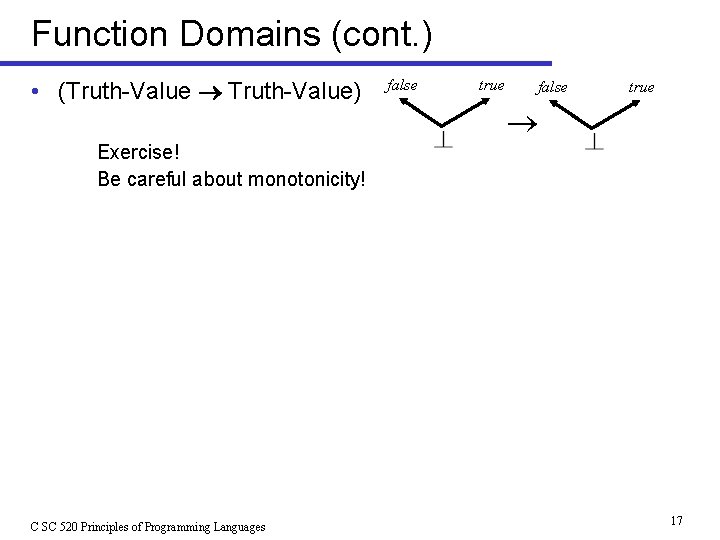
Function Domains (cont. ) • (Truth-Value Truth-Value) false true Exercise! Be careful about monotonicity! C SC 520 Principles of Programming Languages 17

-Calculus • Let e be an expression containing zero or more occurrences of variables • Let denote the result of replacing each occurrence of x by a • The lambda expression n Denotes (names) a function Value of the -expression is a function f such that Provides a direct description of a function object, not indirectly via its behavior when applied to arguments C SC 520 Principles of Programming Languages 18

-Calculus Examples • Example: C SC 520 Principles of Programming Languages 19

-Calculus Examples (cont. ) • Functionals: functions that take other functions as arguments or that return functions; also highertype functions • Example: the definite integral • Example: the indefinite integral C SC 520 Principles of Programming Languages 20

-Calculus Examples (cont. ) • Example: integration routine • Example: summation “operator” C SC 520 Principles of Programming Languages 21

-Calculus Examples (cont. ) • Example: derivative operator • Example: indexing “operator” Postfix [i]: Int. Array Integer [i]= a. a[i] • Example: “funcall” or “apply” operator n n n Signature Combinator definition Lambda definition C SC 520 Principles of Programming Languages 22

Currying (Curry 1945; Schönfinkel 1924) • Transformation reducing a multi-argument function to a cascade of 1 -argument functions • Examples • Applying curry(f) to first argument a yields a partially evaluated function f of its second argument: f(a, -) C SC 520 Principles of Programming Languages 23

Currying (cont. ) • Example: machine language curries n Assume contents(A)=a and contents(B)=b C SC 520 Principles of Programming Languages 24

-Calculus Syntax • Lambda=expression Id=identifier Ab=abstraction Ap=application Lambda Id | Ab | Ap Ab ( Id. Lambda) Ap (Lambda) Id x | y | z | … • Examples C SC 520 Principles of Programming Languages 25

-Calculus: simplified notation • Conventions for dropping () disambiguation needed • Rules for dropping parentheses n Application groups L to R n Application has higher precedence than abstraction n Abstraction groupts R to L n Consecutive abstractions collapse to single n Example: C SC 520 Principles of Programming Languages 26

Variables: Free, Bound, Scope • Metavariables: I: Id L: Lambda • Type the semantic function occurs: Lambda (Id B) • one rule per syntactic case (syntax-driven) n are traditional around syntax argument • Note: In expession x. y the variable x does not occur! C SC 520 Principles of Programming Languages 27

Variables: Free, Bound, Scope (cont. ) • occurs_bound : Lambda (Id B) • occurs_free : Lambda (Id B) C SC 520 Principles of Programming Languages 28

Variables: Free, Bound, Scope (cont. ) • The notions free x, bound x, occur x are relative to a given expression or subexpression • Examples: n n n C SC 520 Principles of Programming Languages 29

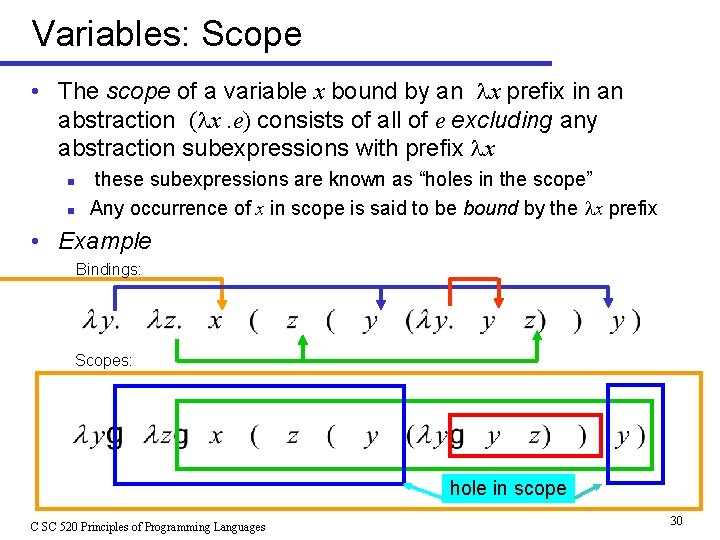
Variables: Scope • The scope of a variable x bound by an x prefix in an abstraction ( x. e) consists of all of e excluding any abstraction subexpressions with prefix x n n these subexpressions are known as “holes in the scope” Any occurrence of x in scope is said to be bound by the x prefix • Example Bindings: Scopes: hole in scope C SC 520 Principles of Programming Languages 30

-calculus: formal computation reduction rules • -conversion: formal parameter names do not affect meaning n Ex: substitute y for free occurrences of x in e (rename of clash occurs) • -reduction: models application of a function abstraction to its argument redex n contractum Ex: C SC 520 Principles of Programming Languages 31

-calculus: formal computation (cont. ) • -reduction: models “extensionality” n x not free in e (no other x occurrences in scope) Ex: C SC 520 Principles of Programming Languages 32

Reduction is locally non-deterministic ? C SC 520 Principles of Programming Languages 33

Normal Forms • • Identify -equivalent expressions Reduction: Reduction “as far as possible”: Defn: Normal Form: an expression that cannot be further reduced by C SC 520 Principles of Programming Languages 34

Normal Forms Don’t Always Exist • Parallel of “non-terminating computation” • Example: “self-application combinator”: • What happens with C SC 520 Principles of Programming Languages 35

Computation Rules • Leftmost Innermost (LI): among the innermost nested redexes, choose the leftmost one to reduce • Leftmost Outermost(LO): among the outermost redexes, choose the letmost one to reduce LO LI C SC 520 Principles of Programming Languages 36

vs --very different • -reduction: abstract e, then apply • -reduction: apply e, then abstract parse no restriction on e not -redex • Example: ((lambda (x) 1+) x) 1+ C SC 520 Principles of Programming Languages not -redex only if e free of x • Example: (lambda (x) (1+ x)) 1+ 37

Mixed and reductions parse C SC 520 Principles of Programming Languages 38

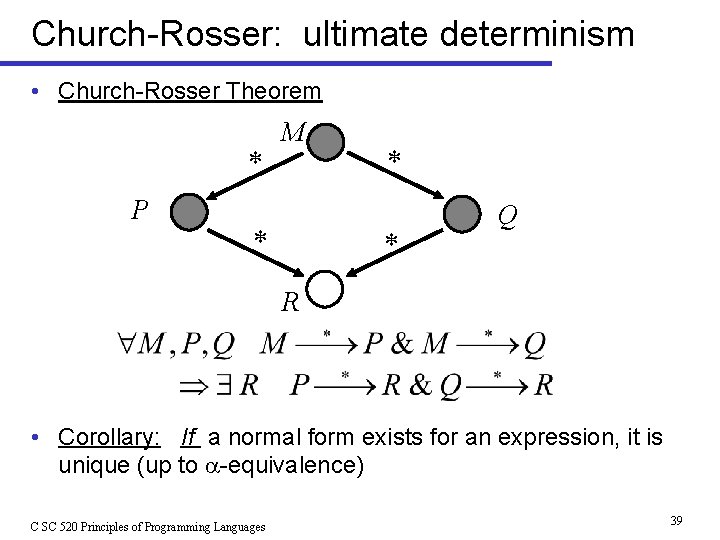
Church-Rosser: ultimate determinism • Church-Rosser Theorem P M Q R • Corollary: If a normal form exists for an expression, it is unique (up to -equivalence) C SC 520 Principles of Programming Languages 39

Church-Rosser: says reduction, not forced LI LO LO LI LI LO LO Correct computation rule: if a normal form , it will be computed—ex: LO LO = normal rule = CBN = lazy Prog Lang: Haskell C SC 520 Principles of Programming Languages LI Incorrect (but efficient): —ex: LI LI = applicative rule = CBV=eager Prog Lang: Scheme 40

Correct Computation Rule • A rule is correct if it calculates a normal form, provided one exists • Theorem: LO (normal rule) is a correct computation rule. n n n LI (applicative rule) is not correct—gives the same result as normal rule whenever it converges to a normal form (guaranteed by the Church-Rosser property) LI is simple, efficient and natural to implement: always evaluate all arguments before evaluating the function LO is very inefficient: performs lots of copying of unevaluated expressions C SC 520 Principles of Programming Languages 41

Typed -calculus • More restrictive reduction. No Type : : = (Type) | Prim. Type Lambda : : = Id | (Lambda) | ( Id : Type. Lambda) Id : : = x | y | z | … Prim. Type : : = int | … • Type Deduction Rules (axiom) (appl) (abst) • E is type correct iff a type such that • Thm: Every type correct expression has a normal form C SC 520 Principles of Programming Languages 42

Typed -calculus (cont. ) • Example: n n is not type correct Work backward using rules. Assume So a contradiction. Therefore there is no consistent type assignment to C SC 520 Principles of Programming Languages 43

Typed -calculus (cont. ) • Example: type the expression n Work forward (appl) (abst) C SC 520 Principles of Programming Languages 44

-Calculus: History • Frege 1893: unary functions suffice for a theory • Schönfinkel 1924: n n n Introduced “currying” Combinators Combinatory (Weak) Completeness: all closed -expressions can be defined in terms of K, S using application only: Let M be built up from , K, S with only x left free. Then an expression F built from K, S only such that Fx=M • Curry 1930: n n introduced axiom of extensionality: Weak Consistency: K=S is not provable C SC 520 Principles of Programming Languages 45

-Calculus: History (cont. ) • Combinatory Completeness Example: Composition functional: n Thm: n Prf: Note that So n and so • Exercise: define C SC 520 Principles of Programming Languages & show 46

-Calculus: History (cont. ) • Church 1932: n If Fx=M call F “ x. M” n Fixed Point Theorem: Given F can construct a such that F n Discovered fixed point (or “paradoxical”) combinator: n Exercise: Define YF and show by reduction that F • Church & Rosser 1936: strong consistency Church. Rosser Property. n n Implies that -equivalence classes of normal forms are disjoint provides a “syntactic model” of computation • Martin-Löf 1972: simplified C-R Theorem’s proof C SC 520 Principles of Programming Languages 47

-Calculus: History (cont. ) • Church 1932: Completeness of the -Calculus n N can be embedded in the -Calculus n n Church 1932/Kleene 1935: recursive definition possible: Check: C SC 520 Principles of Programming Languages 48

-Calculus: History (cont. ) • Church-Rosser Thm (1936) -Calculus functions are ``computable’’ (aka ``recursive”) • Church’s Thesis: The ``effectively computable” functions from N to N are exactly the “ -Calculus definable” functions u a strong assertion about “completeness”; all programming languages since are “complete” in this sense • Evidence accumulated n n Kleene 1936: general recursive -Calculus definable Turing 1937: -Calculus definable Turing-computable Post 1943, Markov 1951, etc. : many more confirmations Any modern programming language C SC 520 Principles of Programming Languages 49

-Calculus: History (cont. ) • Is the untyped -Calculus consistent? Does it have a semantics? What is its semantic domain D? n n n want “data objects” same as “function objects: since Trouble: impossible unless D =1 because Troublesome self-application paradoxes: if we define then n n Dana Scott 1970: will work if we have monotone (and continuous) functions of Above example: is not monotone C SC 520 Principles of Programming Languages the 50

false (false, false) false (false, true) (true, false) false ( , false) false true (true, true) (true, ) ( , true) ( , ) C SC 520 Principles of Programming Languages 51