Principles of MRI Image Formation Allen W Song

Principles of MRI: Image Formation Allen W. Song Brain Imaging and Analysis Center Duke University

What is image formation? To define the spatial location of the sources that contribute to the detected signal.

But MRI does not use projection, reflection, or refraction mechanisms commonly used in optical imaging methods to form image. So how are the MR images formed?

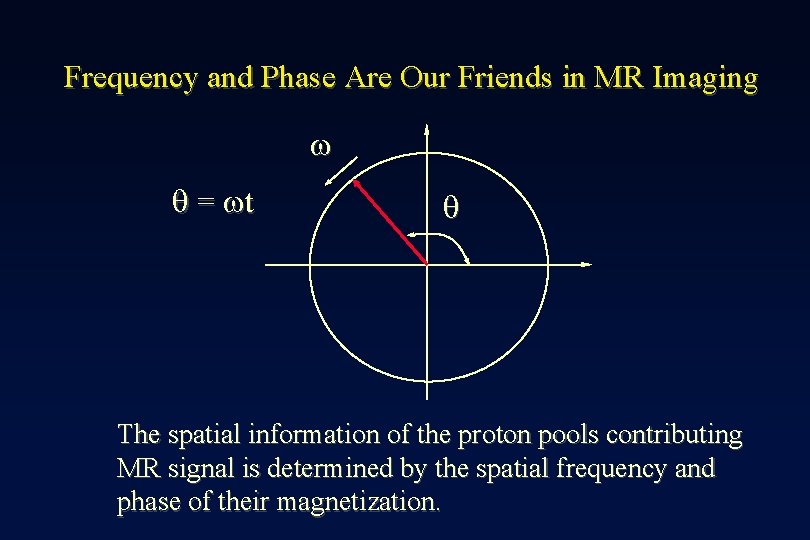
Frequency and Phase Are Our Friends in MR Imaging w q = wt q The spatial information of the proton pools contributing MR signal is determined by the spatial frequency and phase of their magnetization.

Gradient Coils z z z y y x x X gradient y Y gradient x Z gradient Gradient coils generate spatially varying magnetic field so that spins at different location precess at frequencies unique to their location, allowing us to reconstruct 2 D or 3 D images.

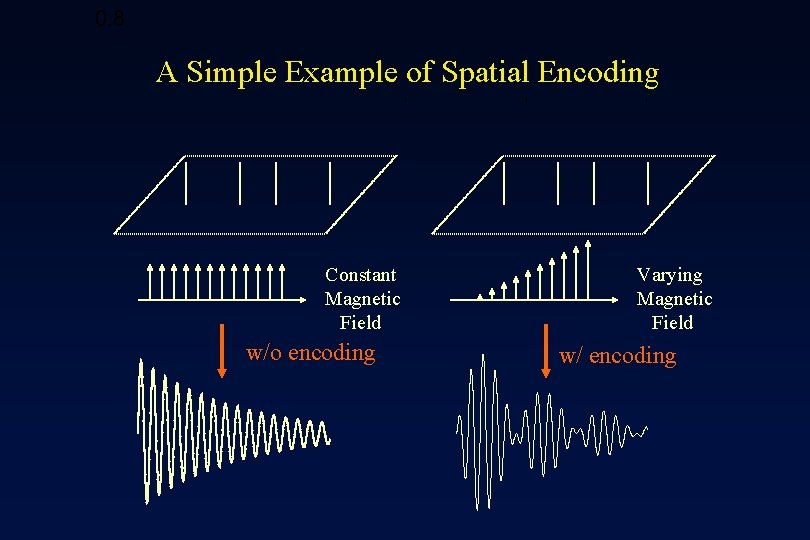
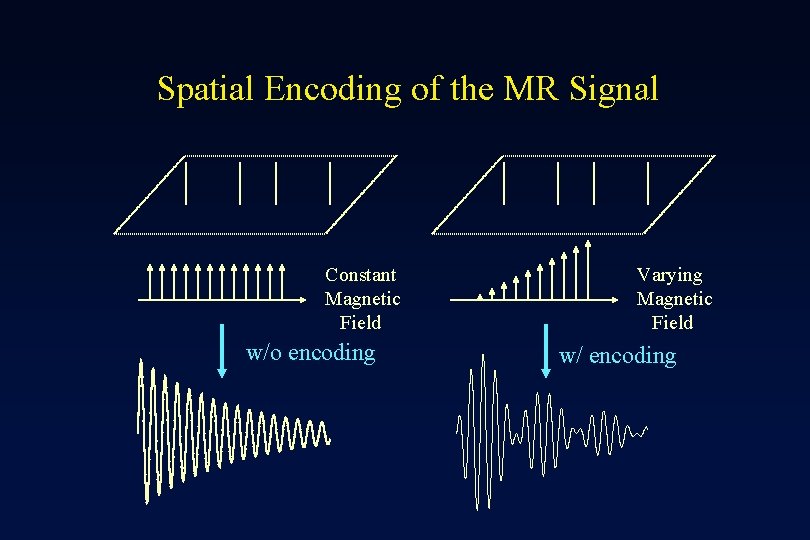
0. 8 A Simple Example of Spatial Encoding Constant Magnetic Field w/o encoding Varying Magnetic Field w/ encoding

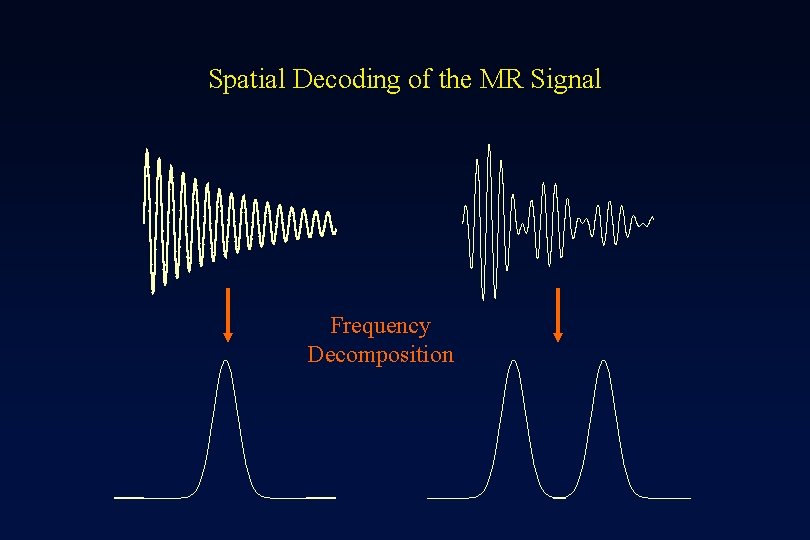
Spatial Decoding of the MR Signal Frequency Decomposition

Steps in 3 D Localization ¨ Can only detect total RF signal from inside the “RF coil” (the detecting antenna) Excite and receive Mxy in a thin (2 D) slice of the subject The RF signal we detect must come from this slice è Reduce dimension from 3 D down to 2 D è Deliberately make magnetic field strength B depend on location within slice Frequency of RF signal will depend on where it comes from è Breaking total signal into frequency components will provide more localization information è Make RF signal phase depend on location within slice

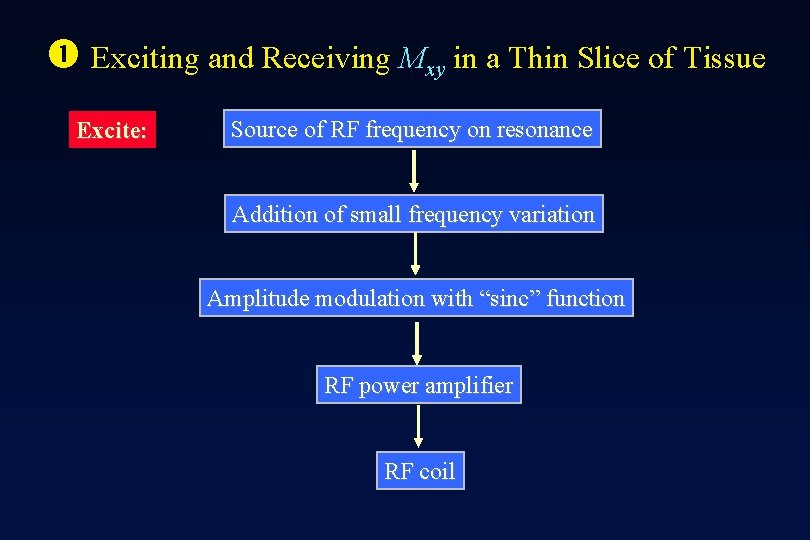
Exciting and Receiving Mxy in a Thin Slice of Tissue Excite: Source of RF frequency on resonance Addition of small frequency variation Amplitude modulation with “sinc” function RF power amplifier RF coil

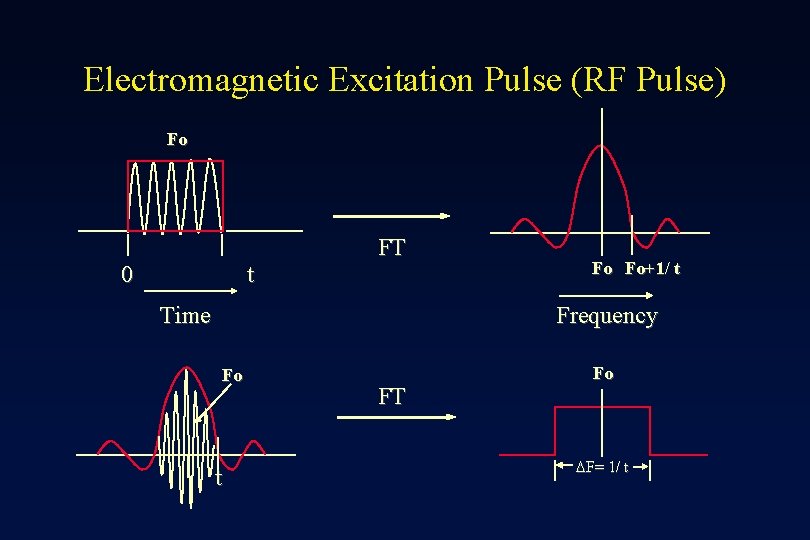
Electromagnetic Excitation Pulse (RF Pulse) Fo 0 t FT Time Fo Fo+1/ t Frequency Fo t FT Fo F= 1/ t

Gradient Fields: Spatially Nonuniform B: ¨During readout (image acquisition) period, turning on gradient field is called frequency encoding --- using a deliberately applied nonuniform field to make the precession frequency depend on location ¨ Before readout (image acquisition) period, turning on gradient field is called phase encoding --- during the readout (image acquisition) period, the effect of gradient field is no longer time-varying, rather it is a fixed phase accumulation determined by the amplitude and duration of the phase encoding gradient. 60 KHz Center frequency [63 MHz at 1. 5 T] Left = – 7 cm f Gx = 1 Gauss/cm = 10 m. Tesla/m = strength of gradient field x-axis Right = +7 cm

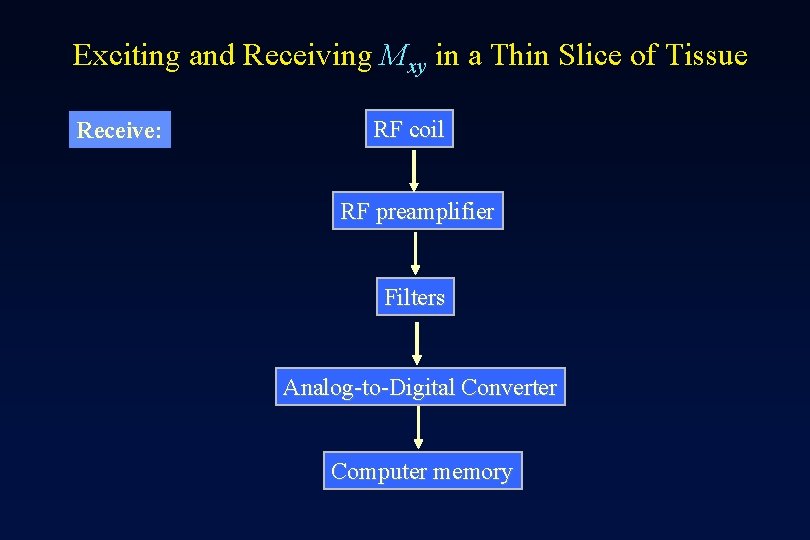
Exciting and Receiving Mxy in a Thin Slice of Tissue Receive: RF coil RF preamplifier Filters Analog-to-Digital Converter Computer memory

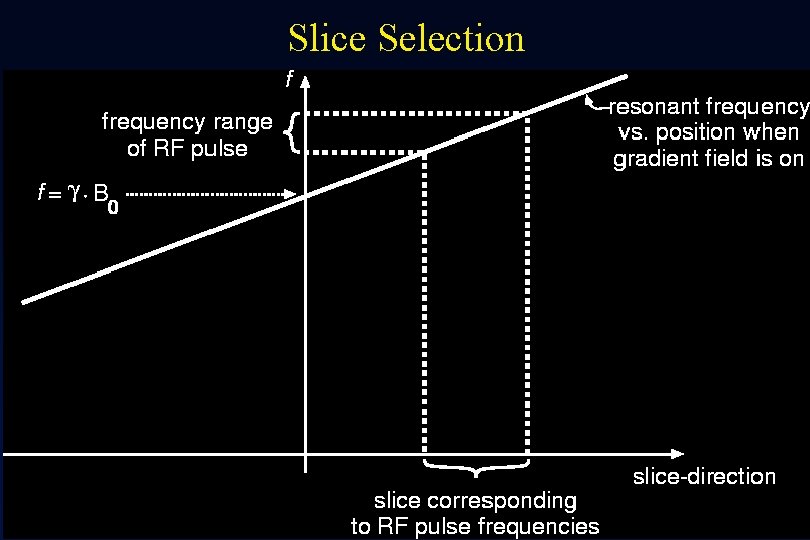
Slice Selection

Slice Selection – along z z

Determining slice thickness Resonance frequency range as the result of slice-selective gradient: F = g. H * Gsl * dsl The bandwidth of the RF excitation pulse: w/2 p Thus the slice thickness can be derived as dsl = w / (g. H * Gsl * 2 p)

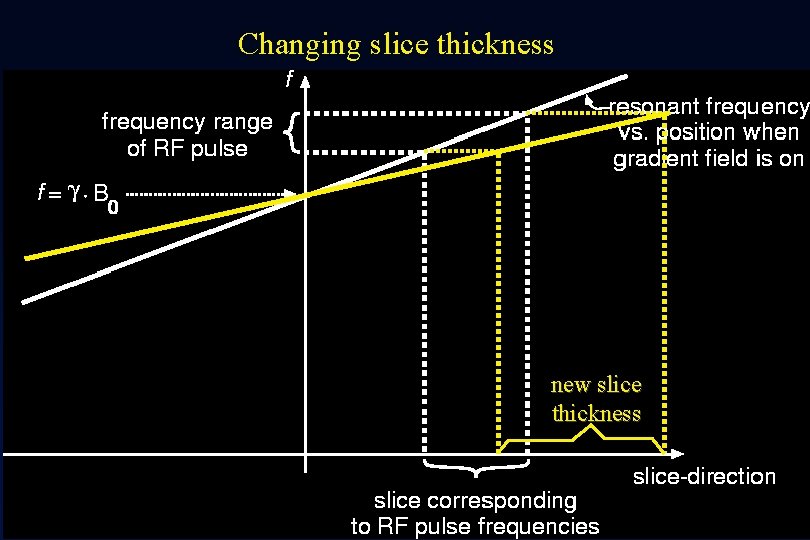
Changing slice thickness There are two ways to do this: (a) Change the slope of the slice selection gradient (b) Change the bandwidth of the RF excitation pulse Both are used in practice, with (a) being more popular

Changing slice thickness new slice thickness

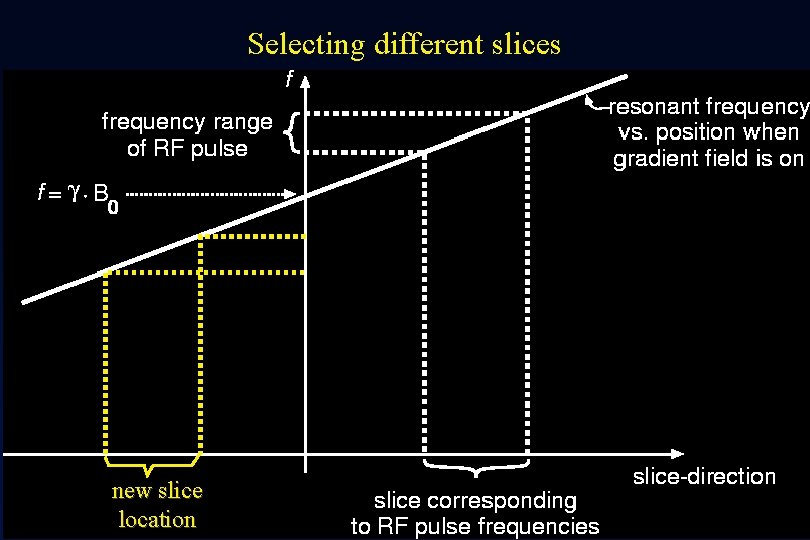
Selecting different slices In theory, there are two ways to select different slices: (a) Change the position of the zero point of the slice selection gradient with respect to isocenter (b) Change the center frequency of the RF to correspond to a resonance frequency at the desired slice F = g. H (Bo + Gsl * Lsl ) Option (b) is usually used as it is not easy to change the isocenter of a given gradient coil.

Selecting different slices new slice location

Readout Localization (frequency encoding) ¨ After RF pulse (B 1) ends, acquisition (readout) of NMR RF signal begins · During readout, gradient field perpendicular to slice selection gradient is turned on · Signal is sampled about once every few microseconds, digitized, and stored in a computer • Readout window ranges from 5– 100 milliseconds (can’t be longer than about 2 T 2*, since signal dies away after that) · Computer breaks measured signal V(t) into frequency components v(f ) — using the Fourier transform · Since frequency f varies across subject in a known way, we can assign each component v(f ) to the place it comes from

Spatial Encoding of the MR Signal Constant Magnetic Field w/o encoding Varying Magnetic Field w/ encoding

It’d be easy if we image with only 2 voxels … But often times we have imaging matrix at 256 or higher.

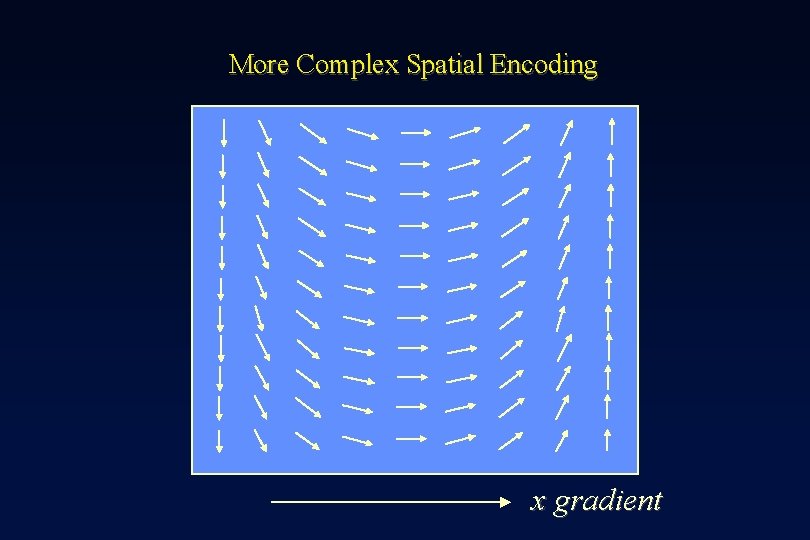
More Complex Spatial Encoding x gradient

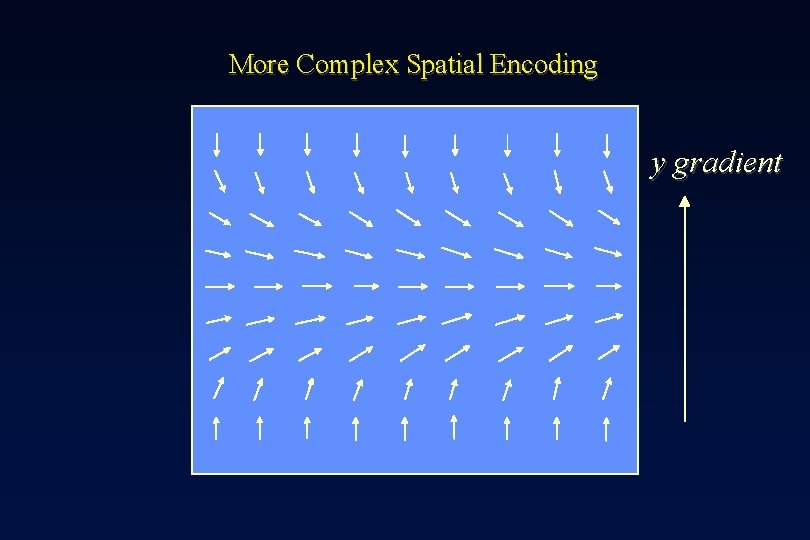
More Complex Spatial Encoding y gradient

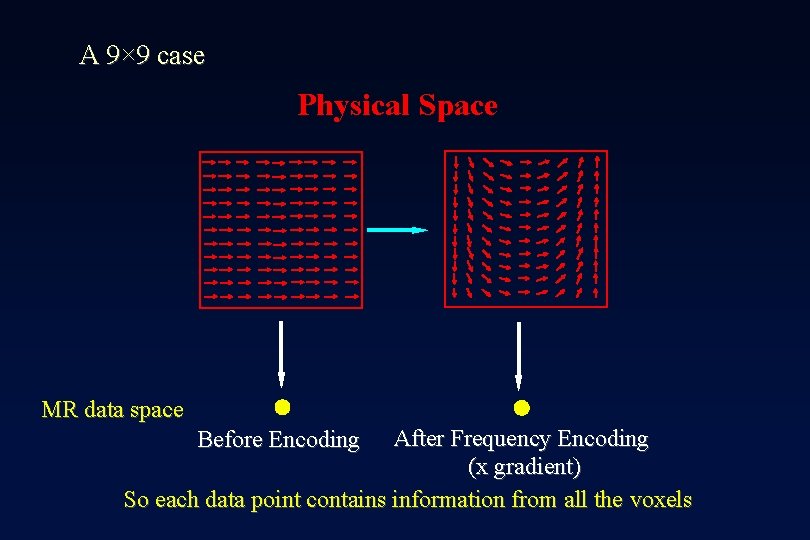
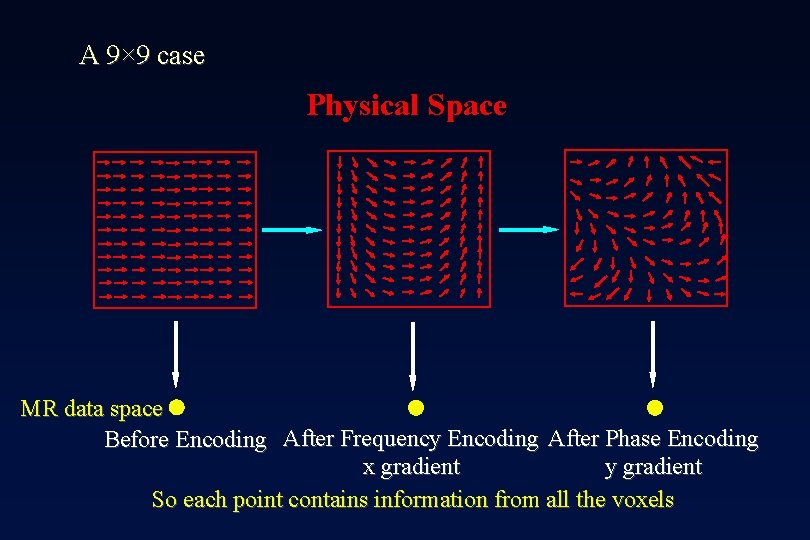
A 9× 9 case Physical Space MR data space After Frequency Encoding (x gradient) So each data point contains information from all the voxels Before Encoding

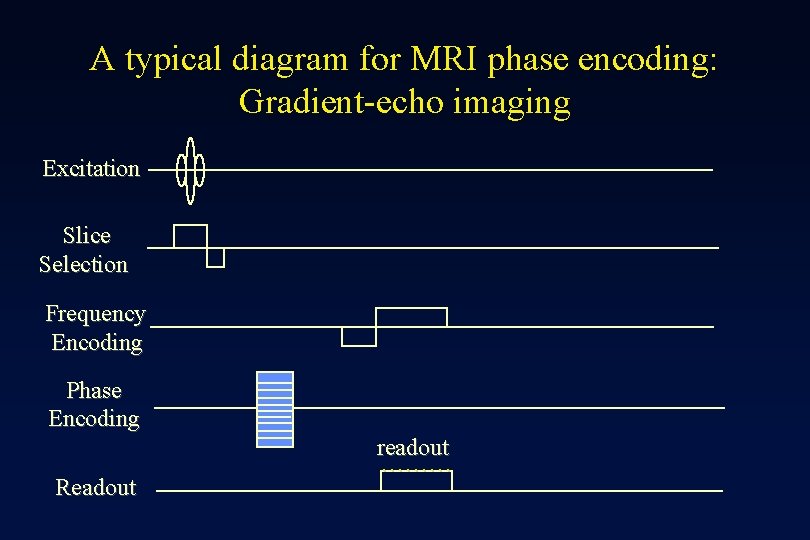
A typical diagram for MRI frequency encoding: Gradient-echo imaging Excitation Slice Selection TE Frequency Encoding Readout Time point #1 readout ……… Time point #9 Data points collected during this period corrspond to one-line in k-space

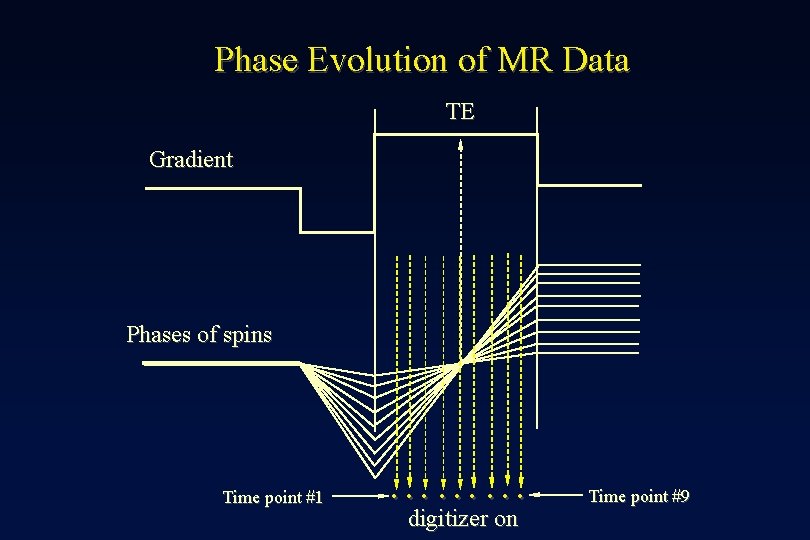
Phase Evolution of MR Data TE Gradient Phases of spins Time point #1 ……… digitizer on Time point #9

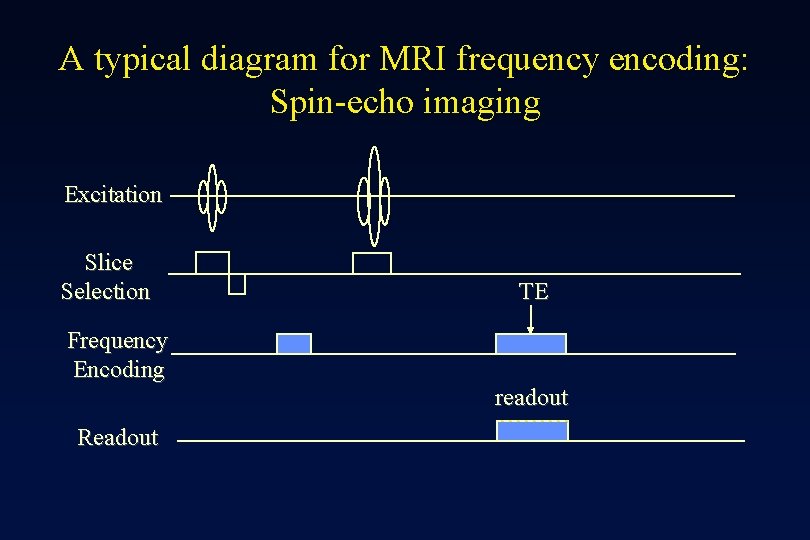
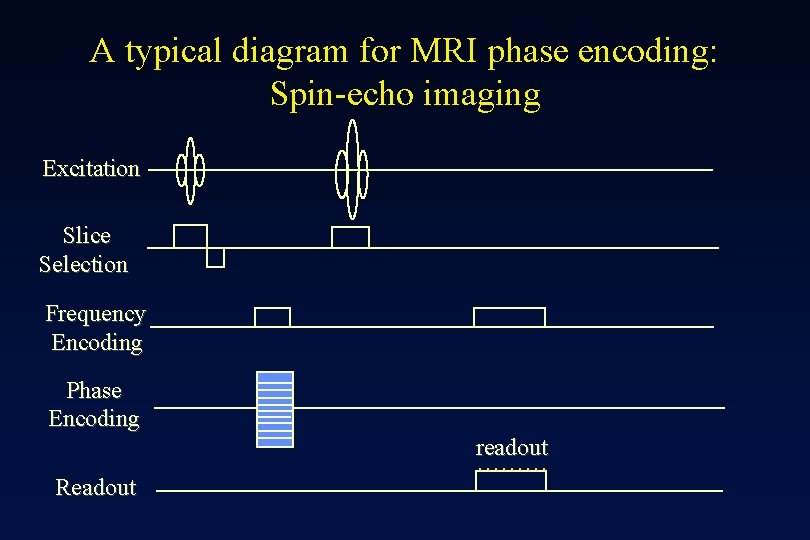
A typical diagram for MRI frequency encoding: Spin-echo imaging Excitation Slice Selection TE Frequency Encoding Readout readout ………

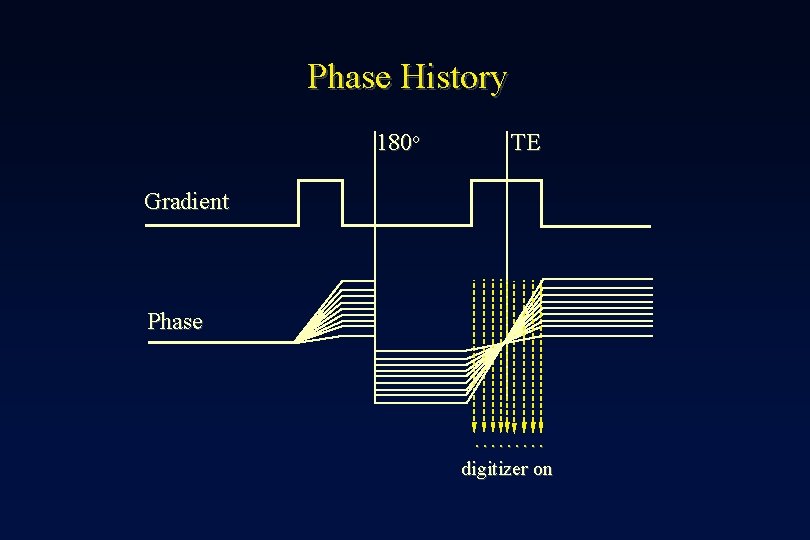
Phase History 180 o TE Gradient Phase ……… digitizer on

Image Resolution (in Plane) ¨ Spatial resolution depends on how well we can separate frequencies in the data V(t) · Resolution is proportional to f = frequency accuracy · Stronger gradients nearby positions are better separated in frequencies resolution can be higher for fixed f · Longer readout times can separate nearby frequencies better in V(t) because phases of cos(f t) and cos([f+ f] t) will be more different

Calculation of the Field of View (FOV) along frequency encoding direction g* Gf * FOVf = BW = 1/ t Which means FOVf = 1/ (g Gf t) where BW is the bandwidth for the receiver digitizer.

The Second Dimension: Phase Encoding ¨ Slice excitation provides one localization dimension ¨ Frequency encoding provides second dimension ¨ The third dimension is provided by phase encoding: · We make the phase of Mxy (its angle in the xy-plane) signal depend on location in the third direction · This is done by applying a gradient field in the third direction ( to both slice select and frequency encode) · Fourier transform measures phase of each v(f ) component of V(t), as well as the frequency f · By collecting data with many different amounts of phase encoding strength, can break each v(f ) into phase components, and so assign them to spatial locations in 3 D

A 9× 9 case Physical Space MR data space Before Encoding After Frequency Encoding After Phase Encoding y gradient x gradient So each point contains information from all the voxels

A typical diagram for MRI phase encoding: Gradient-echo imaging Excitation Slice Selection Frequency Encoding Phase Encoding Readout readout ………

A typical diagram for MRI phase encoding: Spin-echo imaging Excitation Slice Selection Frequency Encoding Phase Encoding Readout readout ………

Calculation of the Field of View (FOV) along phase encoding direction g* Gp * FOVp = Np / Tp Which means FOVp = 1/ (g Gp Tp/Np) = 1/ (g Gp t) where Tp is the duration and Np the number of the phase encoding gradients, Gp is the maximum amplitude of the phase encoding gradient.

Part II. 2 Introduction to k-space (MR data space) Image k-space

Phase Encode Step 1 Time point #2 Time point #3 Phase Encode Step 2 Time point #1 Time point #2 Time point #3 Phase Encode Step 3 Time point #1 Time point #2 Time point #3 ……. .

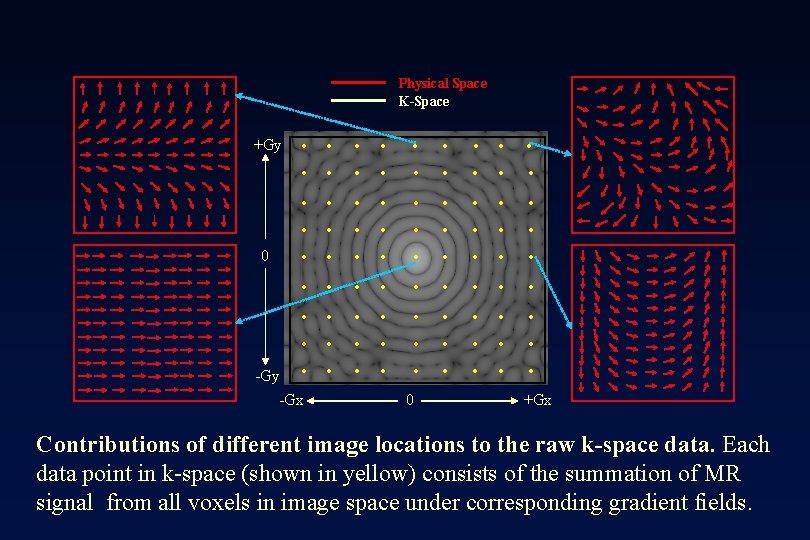
+Gy 0 . . . . -Gy -Gx . . . . Physical Space K-Space . . 0 . . +Gx Contributions of different image locations to the raw k-space data. Each data point in k-space (shown in yellow) consists of the summation of MR signal from all voxels in image space under corresponding gradient fields.

Acquired MR Signal For a given data point in k-space, say (kx, ky), its signal S(kx, ky) is the sum of all the little signal from each voxel I(x, y) in the physical space, under the gradient field at that particular moment From this equation, it can be seen that the acquired MR signal, which is also in a 2 -D space (with kx, ky coordinates), is the Fourier Transform of the imaged object. Kx = g/2 p 0 t Gx(t) dt Ky = g/2 p 0 t Gy(t) dt

Two Spaces k-space ky IFT kx Acquired Data Image space y x FT Final Image

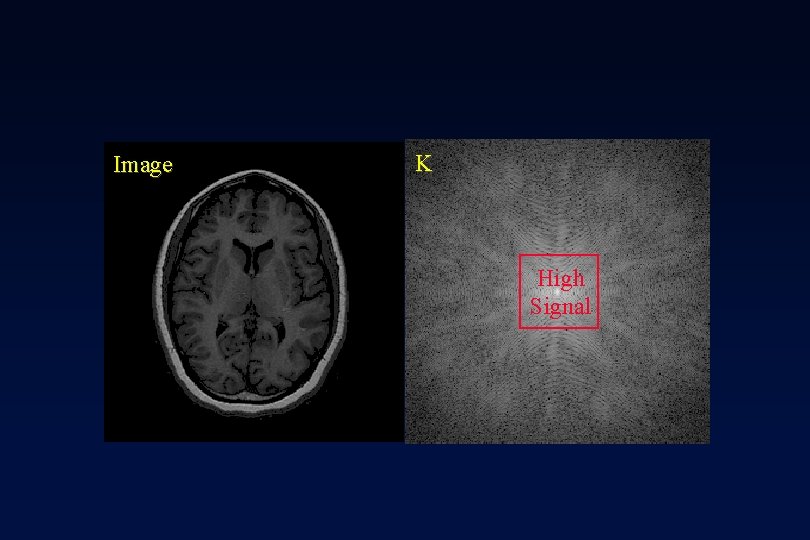
Image K High Signal

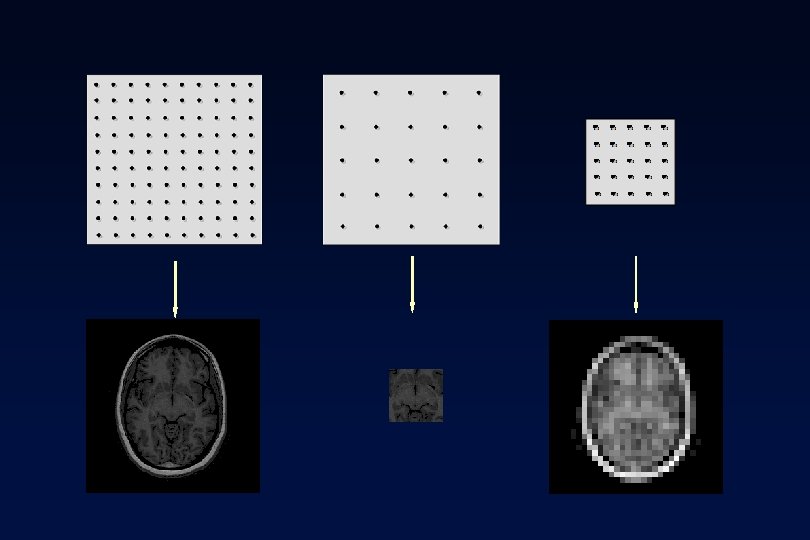
Full Image Full k-space Intensity-Heavy Image Lower k-space Detail-Heavy Image Higher k-space

The k-space Trajectory Equations that govern k-space trajectory: Kx = g/2 p 0 t Gx(t) dt Ky = g/2 p 0 t Gy(t) dt Gx (amplitude) Kx (area) 0 t time

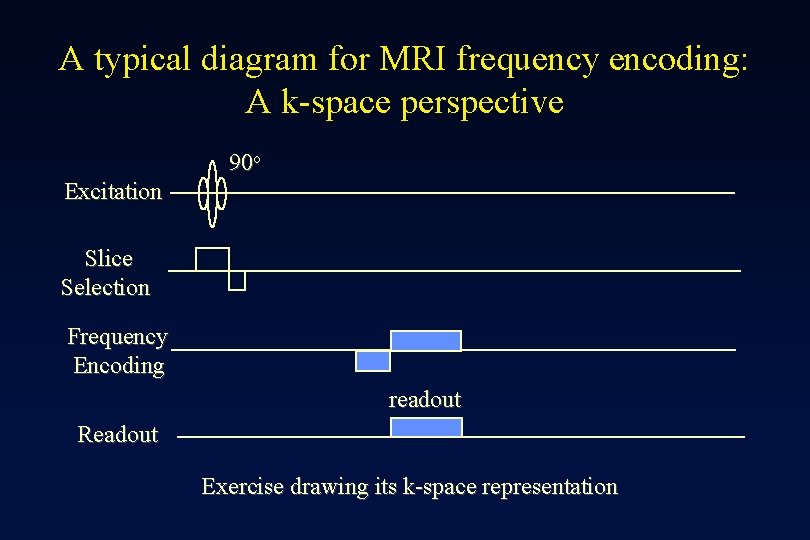
A typical diagram for MRI frequency encoding: A k-space perspective 90 o Excitation Slice Selection Frequency Encoding readout Readout Exercise drawing its k-space representation

The k-space Trajectory

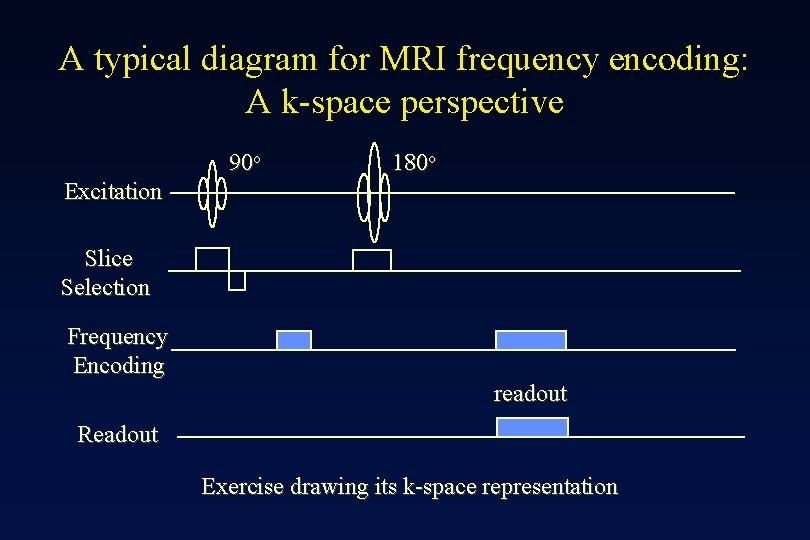
A typical diagram for MRI frequency encoding: A k-space perspective 90 o 180 o Excitation Slice Selection Frequency Encoding readout Readout Exercise drawing its k-space representation

The k-space Trajectory

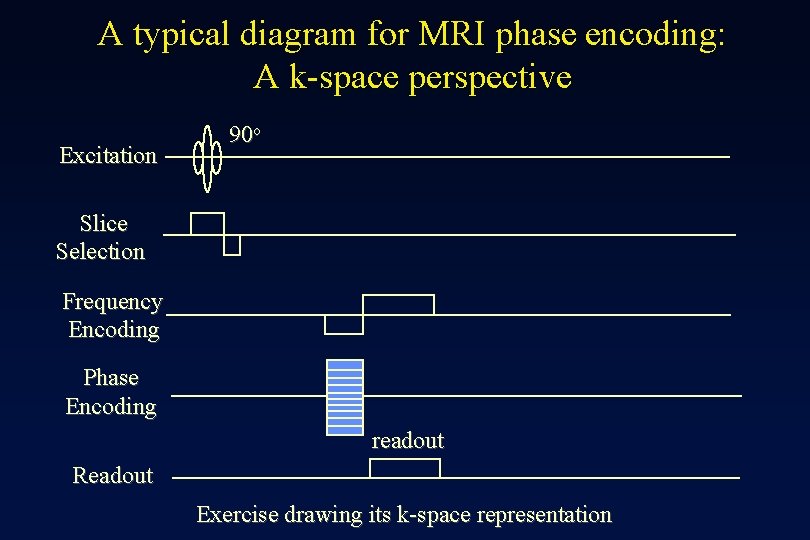
A typical diagram for MRI phase encoding: A k-space perspective Excitation 90 o Slice Selection Frequency Encoding Phase Encoding readout Readout Exercise drawing its k-space representation

The k-space Trajectory

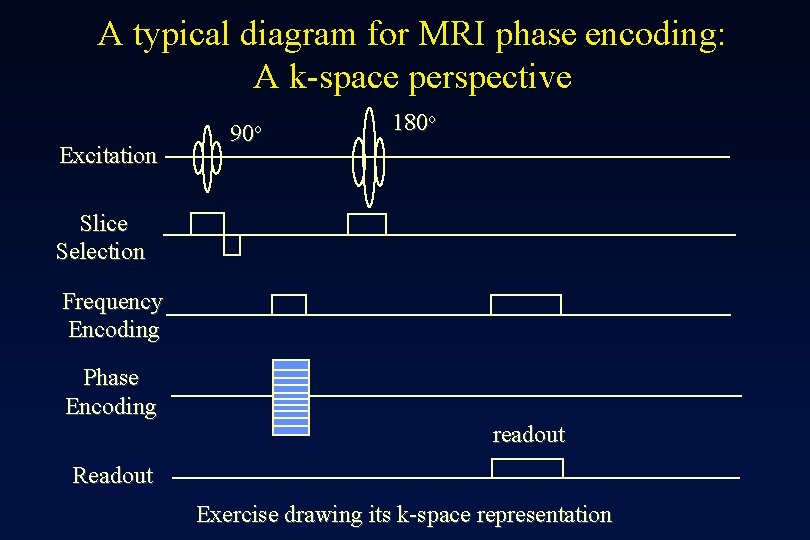
A typical diagram for MRI phase encoding: A k-space perspective Excitation 90 o 180 o Slice Selection Frequency Encoding Phase Encoding readout Readout Exercise drawing its k-space representation

The k-space Trajectory

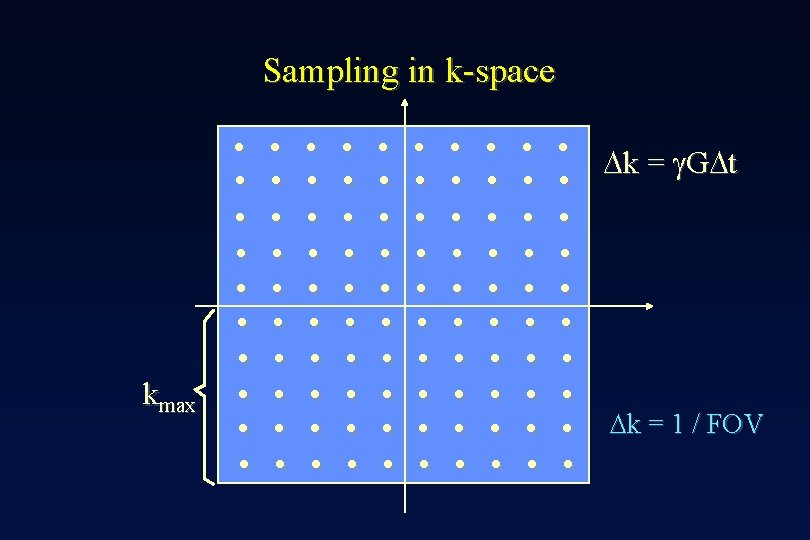
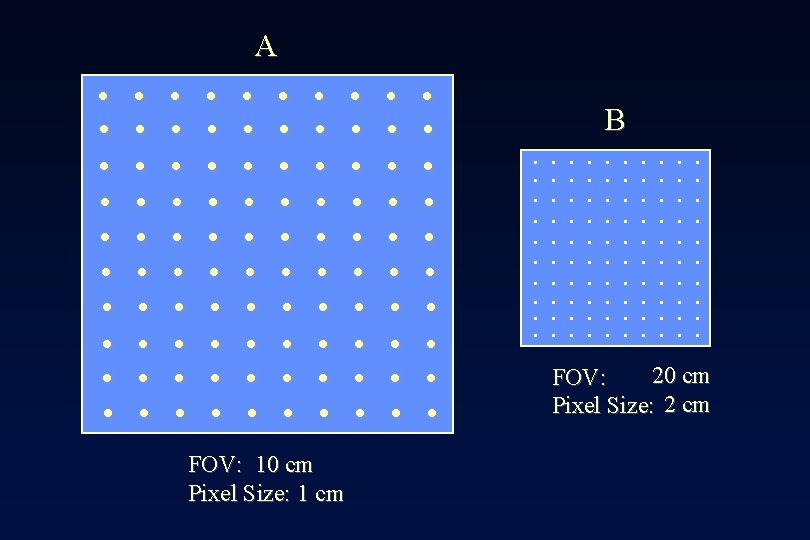
Sampling in k-space kmax . . . . . . k = g. G t k = 1 / FOV

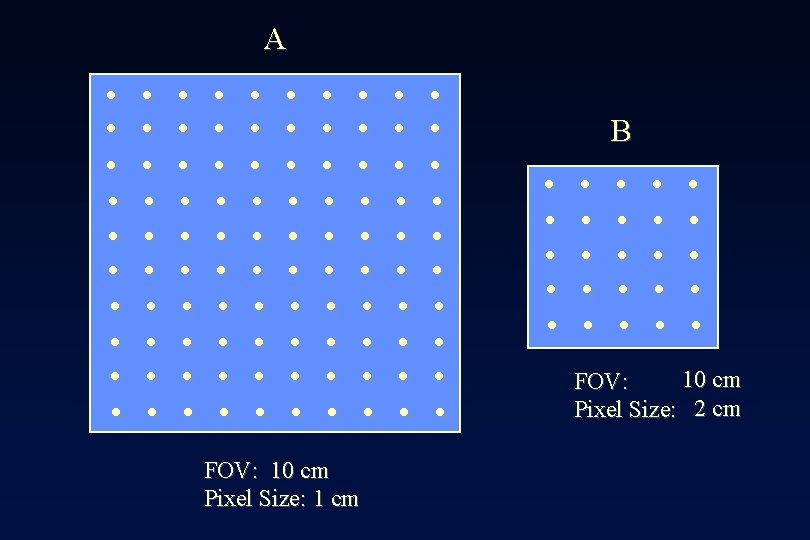
A . . . . . . FOV: 10 cm Pixel Size: 1 cm B . . . 10 cm FOV: Pixel Size: 2 cm

A . . . . . . FOV: 10 cm Pixel Size: 1 cm . . B . . 5 cm FOV: Pixel Size: 1 cm . . .

A . . . . . . FOV: 10 cm Pixel Size: 1 cm B . . . . . . 20 cm FOV: Pixel Size: 2 cm

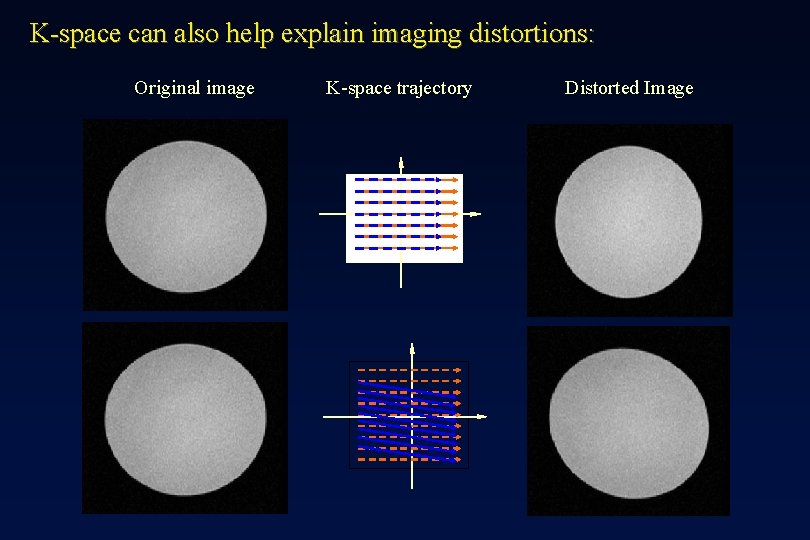
K-space can also help explain imaging distortions: Original image K-space trajectory Distorted Image