Principles Learn The Method Principles Basics should be

Principles Learn The Method

Principles Basics should be automatic Memorize and Practice!

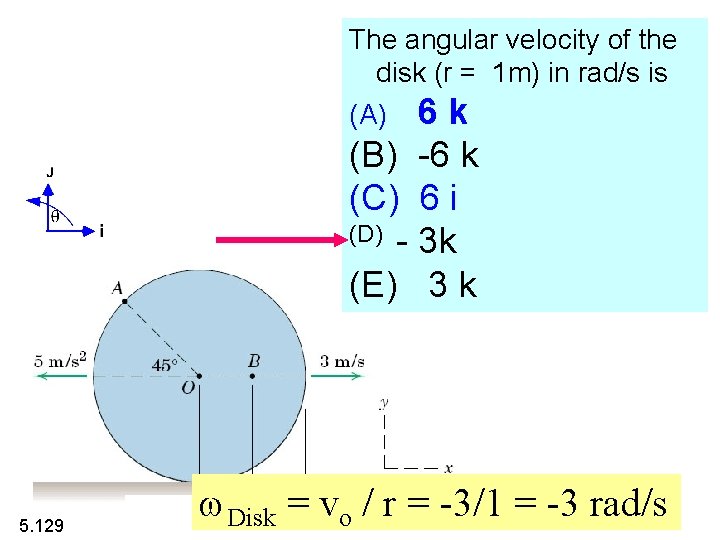
The angular velocity of the disk (r = 1 m) in rad/s is (A) 6 k (B) -6 k (C) 6 i (D) - 3 k (E) 3 k 5. 129 w. Disk = vo / r = -3/1 = -3 rad/s

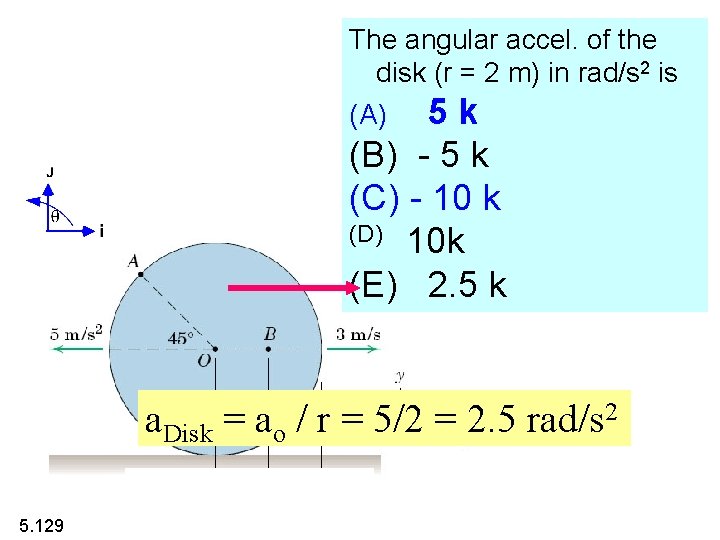
The angular accel. of the disk (r = 2 m) in rad/s 2 is (A) 5 k (B) - 5 k (C) - 10 k (D) 10 k (E) 2. 5 k a. Disk = ao / r = 5/2 = 2. 5 rad/s 2 5. 129

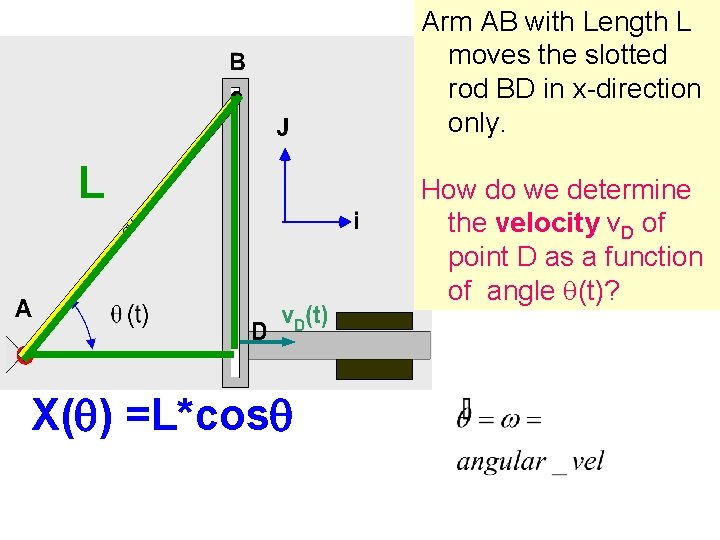
Arm AB with Length L moves the slotted rod BD in x-direction only. L X(q) =L*cosq How do we determine the velocity v. D of point D as a function of angle q(t)?

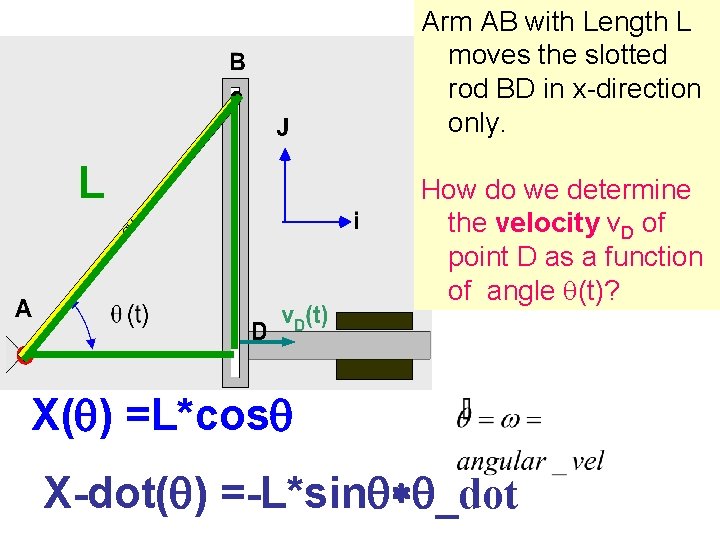
Arm AB with Length L moves the slotted rod BD in x-direction only. L How do we determine the velocity v. D of point D as a function of angle q(t)? X(q) =L*cosq X-dot(q) =-L*sinq*q_dot

Chapter 14 Energy Methods

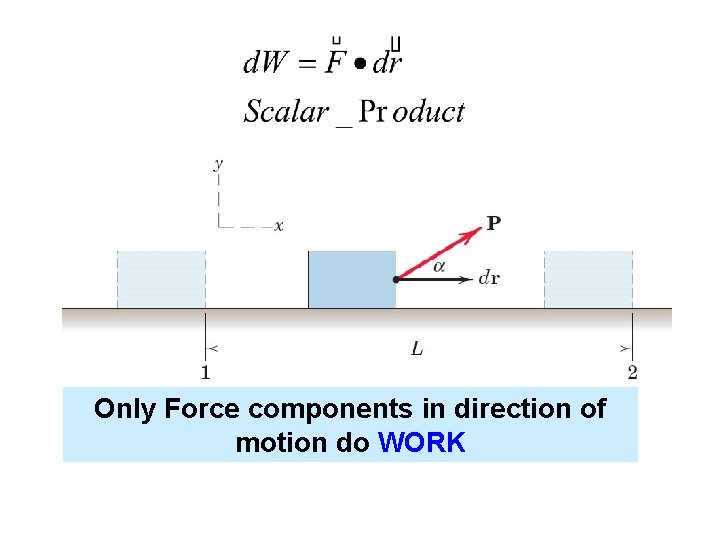
Only Force components in direction of motion do WORK

The work-energy relation: The relation between the work done on a particle by the forces which are applied on it and how its kinetic energy changes follows from Newton’s second law.

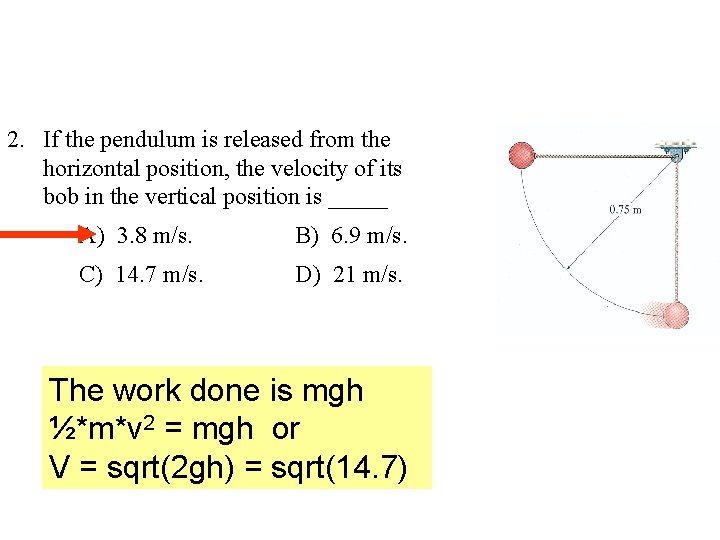
2. If the pendulum is released from the horizontal position, the velocity of its bob in the vertical position is _____ A) 3. 8 m/s. B) 6. 9 m/s. C) 14. 7 m/s. D) 21 m/s. The work done is mgh ½*m*v 2 = mgh or V = sqrt(2 gh) = sqrt(14. 7)

Power Units of power: J/sec = Nm/sec = Watts 1 hp = 746 W

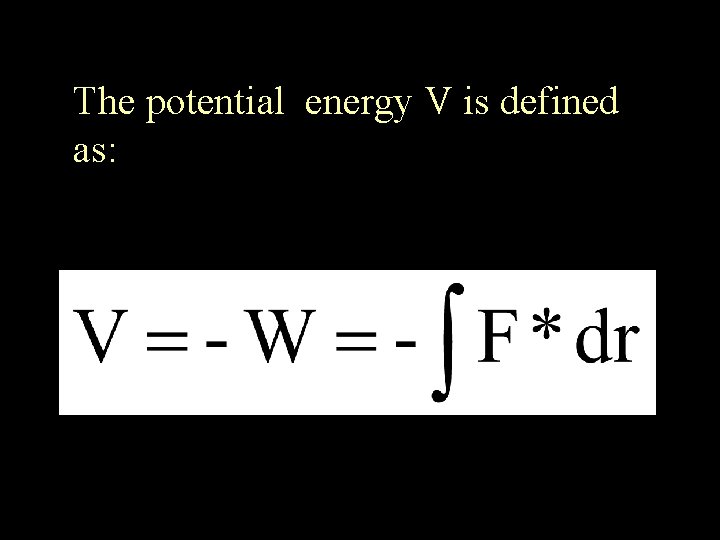
The potential energy V is defined as:

Conservative Forces T 1 + V 1 = T 2 + V 2

Potential Energy Potential energy is energy which results from position or configuration. An object may have the capacity for doing work as a result of its position in a gravitational field. It may have elastic potential energy as a result of a stretched spring or other elastic deformation.

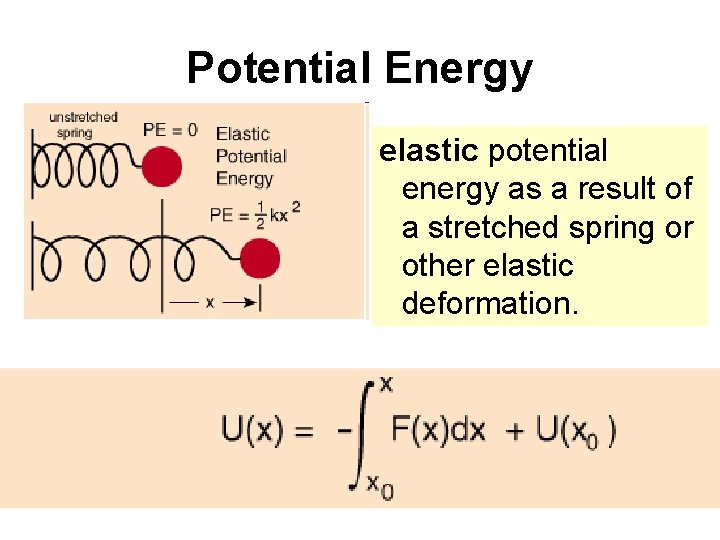
Potential Energy elastic potential energy as a result of a stretched spring or other elastic deformation.

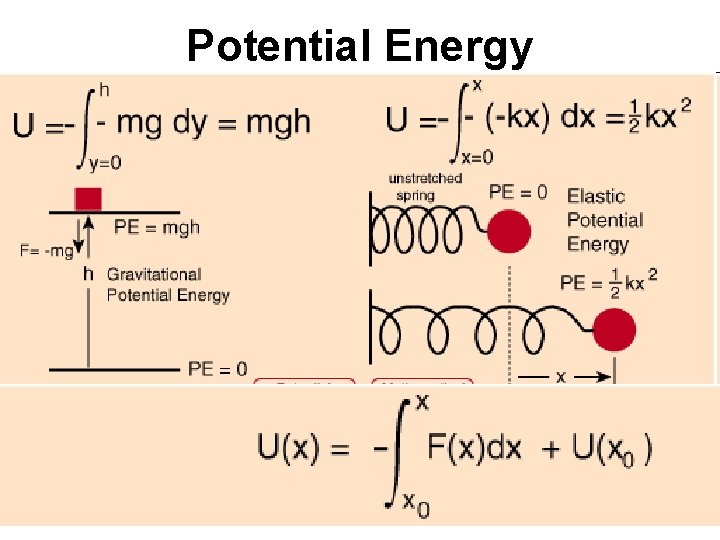
Potential Energy

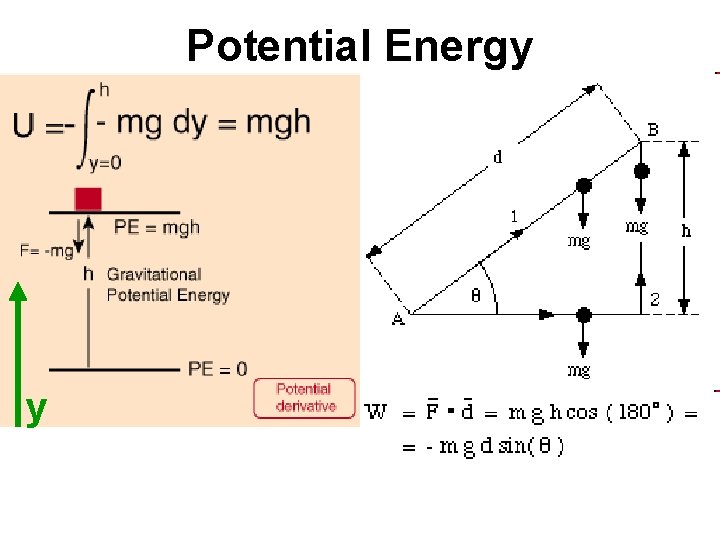
Potential Energy y

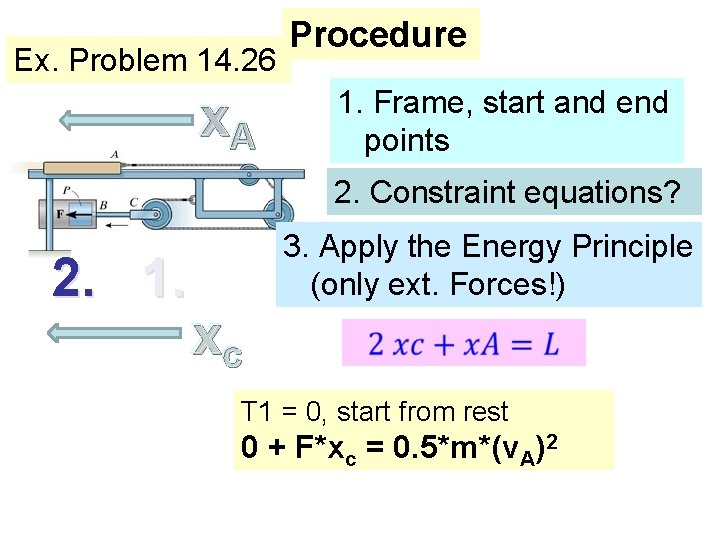
Ex. Problem 14. 26 x. A Procedure 1. Frame, start and end points 2. Constraint equations? 2. 1. 3. Apply the Energy Principle (only ext. Forces!) xc T 1 = 0, start from rest 0 + F*xc = 0. 5*m*(v. A)2

Chapter 16 Rigid Body Kinematics

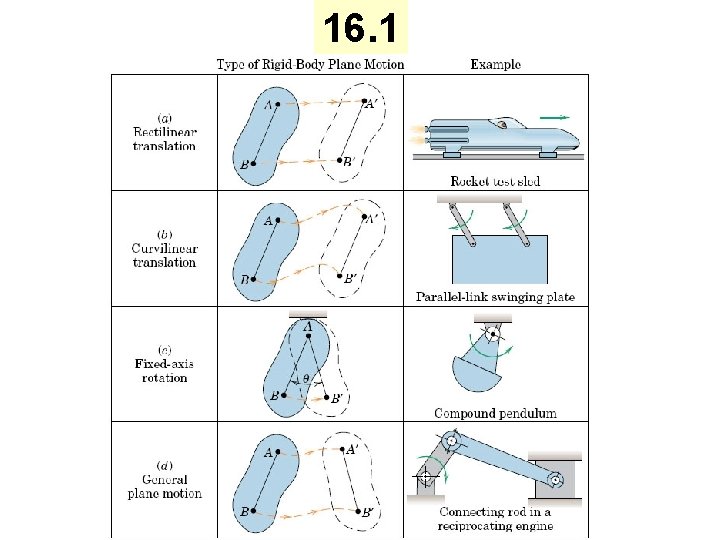
16. 1

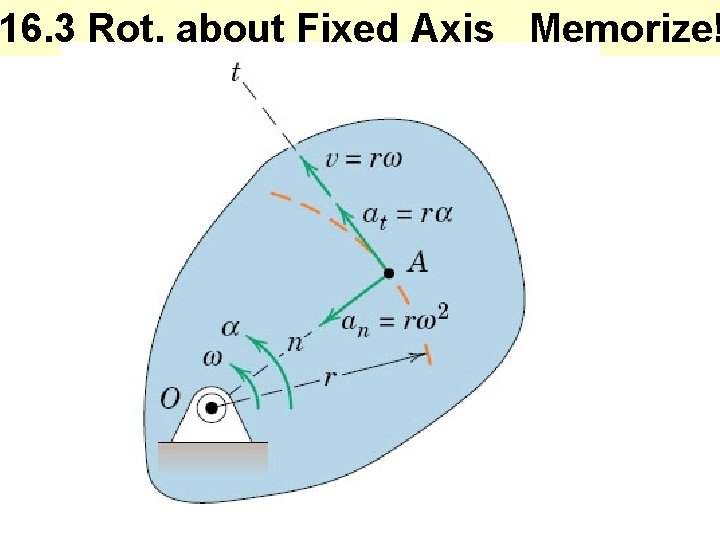
16. 3 Rot. about Fixed Axis Memorize!

Vector Product is NOT commutative!

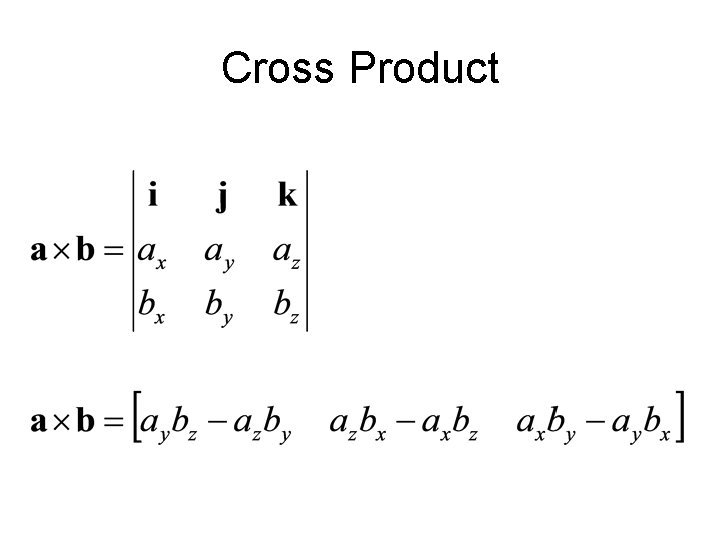
Cross Product

Derivative of a Rotating Vector • vector r is rotating around the origin, maintaining a fixed distance • At any instant, it has an angular velocity of ω

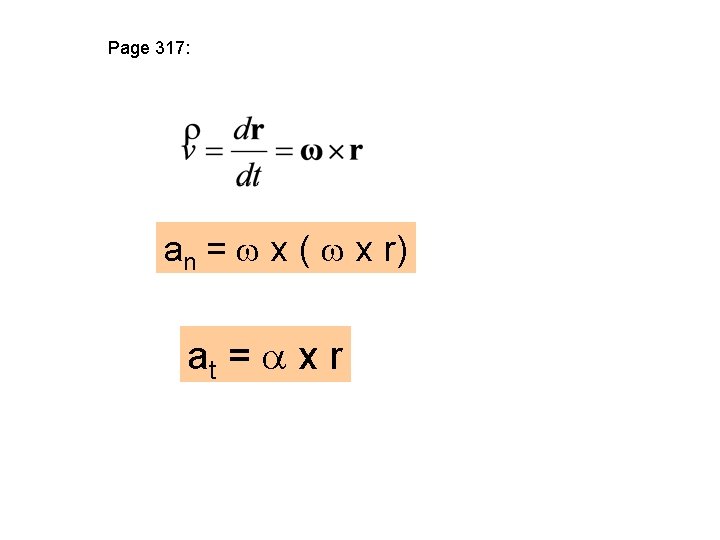
Page 317: an = w x ( w x r) at = a x r

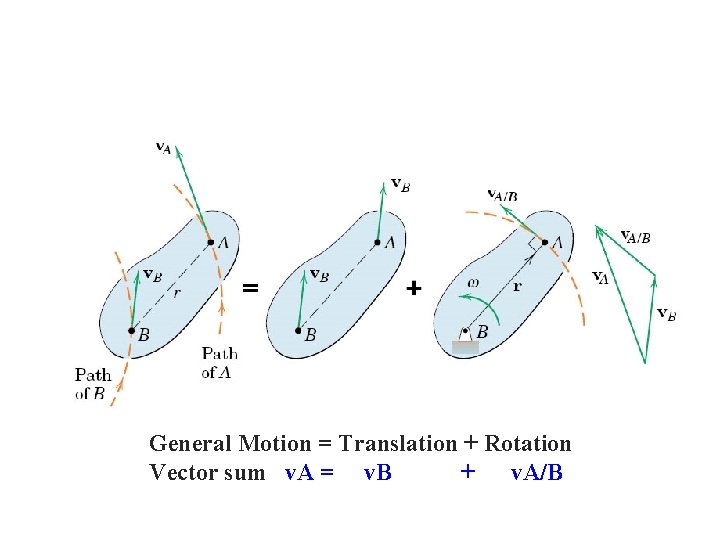
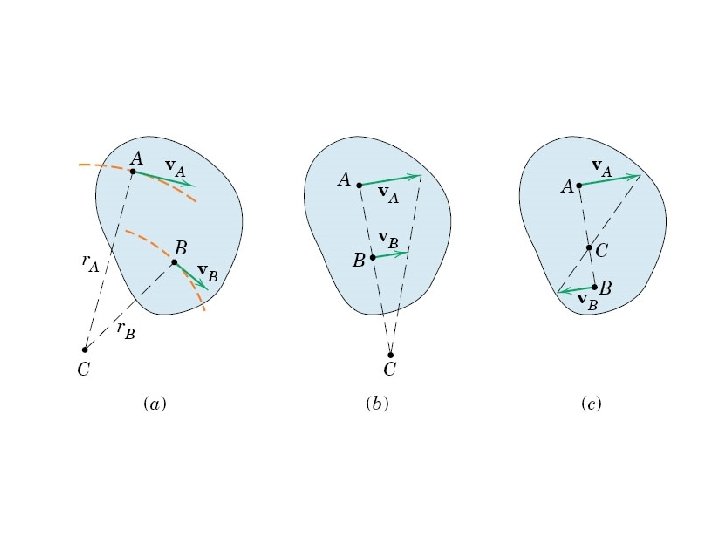
General Motion = Translation + Rotation Vector sum v. A = v. B + v. A/B

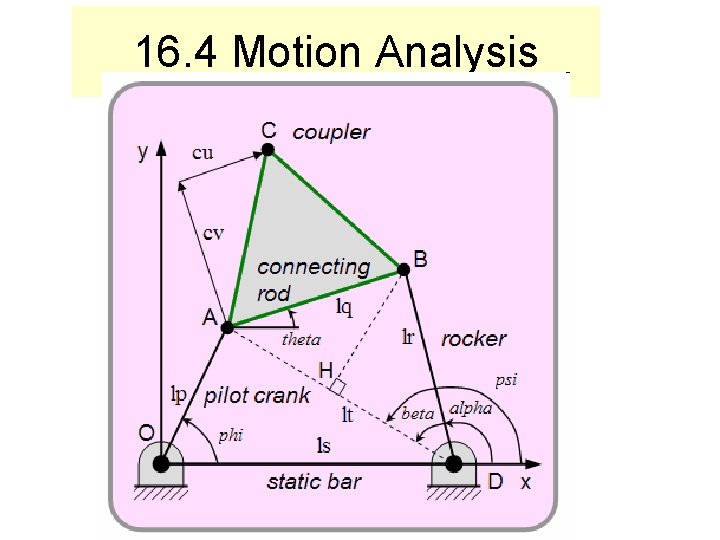
16. 4 Motion Analysis

Approach 1. Geometry: Definitions Constants Variables Make a sketch 2 a. Analysis (16. 4) Derivatives (velocity 2 b. Rel. Motion (16. 5) and acceleration) 3. Equations of Motion 4. Solve the Set of Equations. Use Computer Tools.

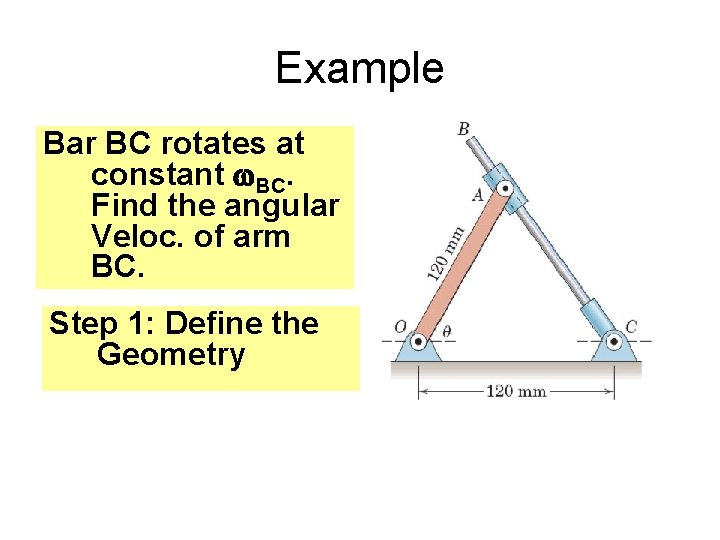
Example Bar BC rotates at constant w. BC. Find the angular Veloc. of arm BC. Step 1: Define the Geometry

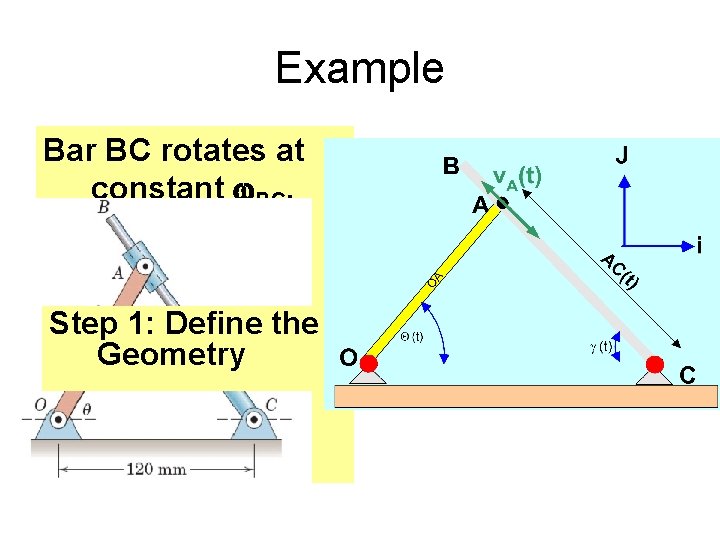
Example Bar BC rotates at constant w. BC. Find the ang. Veloc. of arm BC. Step 1: Define the Geometry

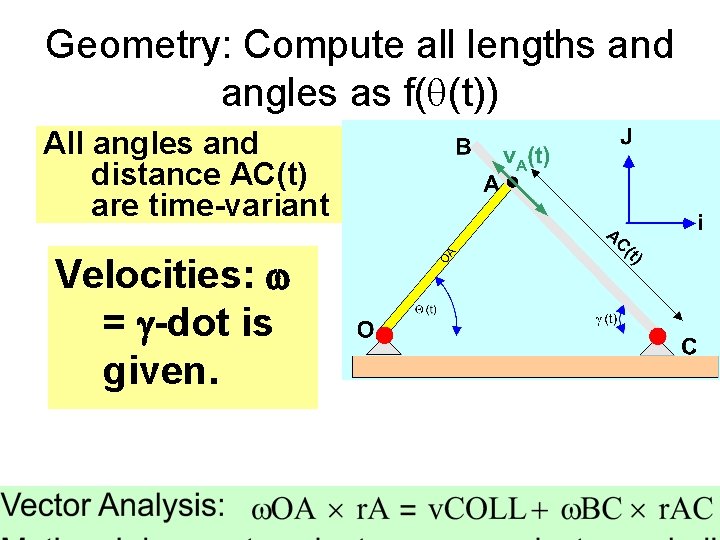
Geometry: Compute all lengths and angles as f(q(t)) All angles and distance AC(t) are time-variant Velocities: w = g-dot is given.

Rigid Body Acceleration Chapter 16. 7 Stresses and Flow Patterns in a Steam Turbine FEA Visualization (U of Stuttgart)

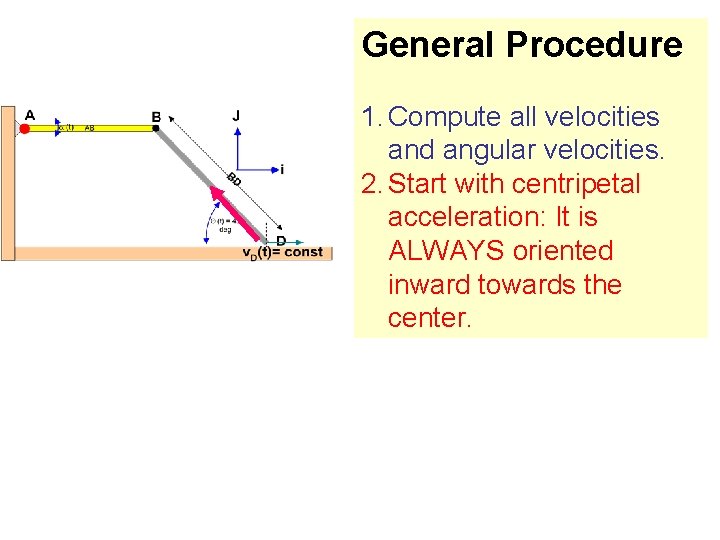
General Procedure 1. Compute all velocities and angular velocities. 2. Start with centripetal acceleration: It is ALWAYS oriented inward towards the center.

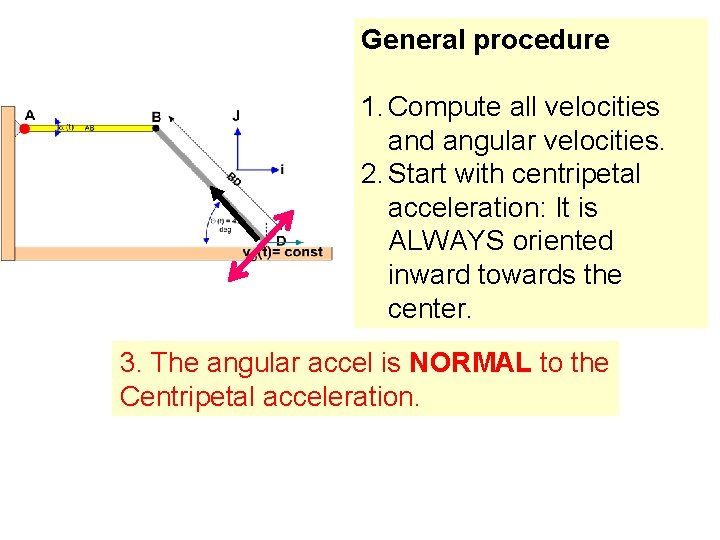
General procedure 1. Compute all velocities and angular velocities. 2. Start with centripetal acceleration: It is ALWAYS oriented inward towards the center. 3. The angular accel is NORMAL to the Centripetal acceleration.

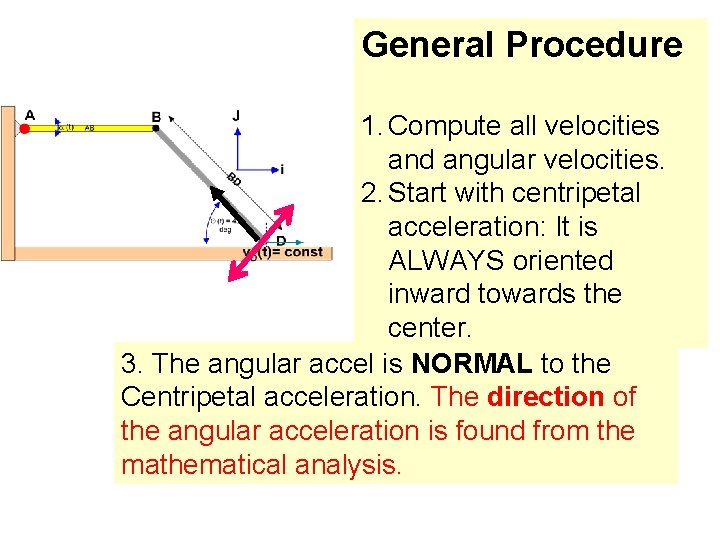
General Procedure 1. Compute all velocities and angular velocities. 2. Start with centripetal acceleration: It is ALWAYS oriented inward towards the center. 3. The angular accel is NORMAL to the Centripetal acceleration. The direction of the angular acceleration is found from the mathematical analysis.

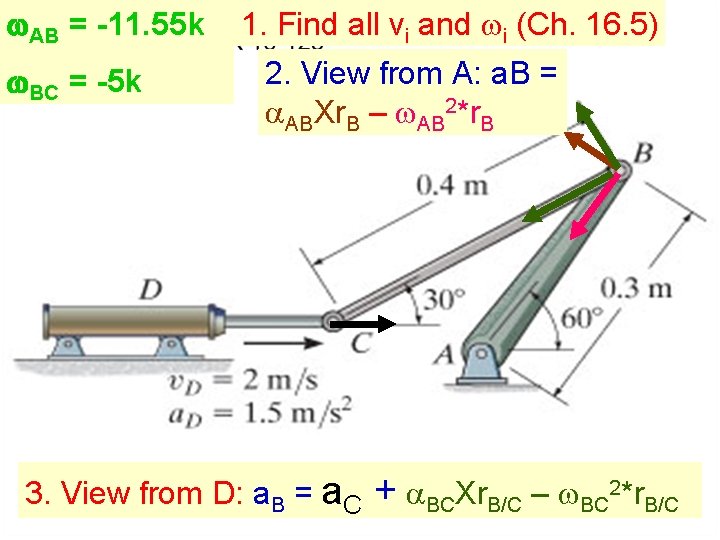
w. AB = -11. 55 k w. BC = -5 k 1. Find all vi and wi (Ch. 16. 5) 2. View from A: a. B = a. ABXr. B – w. AB 2*r. B 3. View from D: a. B = a. C + a. BCXr. B/C – w. BC 2*r. B/C

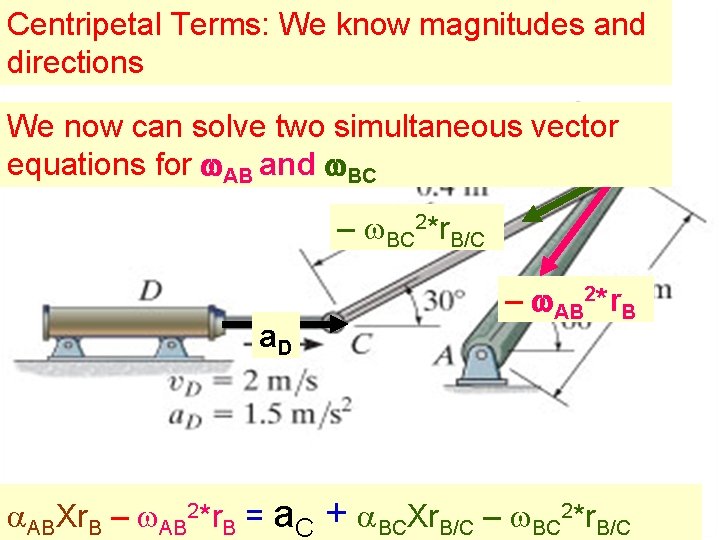
Centripetal Terms: We know magnitudes and directions We now can solve two simultaneous vector equations for w. AB and w. BC – w. BC 2*r. B/C a. D – w. AB 2*r. B a. ABXr. B – w. AB 2*r. B = a. C + a. BCXr. B/C – w. BC 2*r. B/C

a. ABXr. B – w. AB 2*r. B = a. C + a. BCXr. B/C – w. BC 2*r. B/C

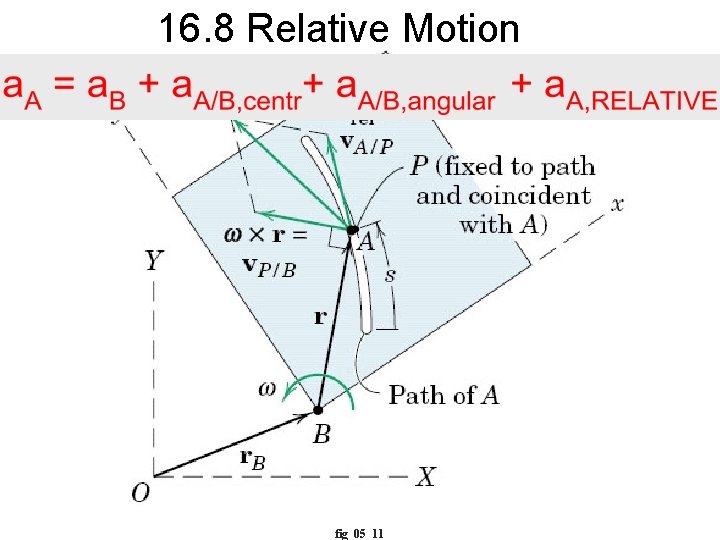
16. 8 Relative Motion fig_05_11

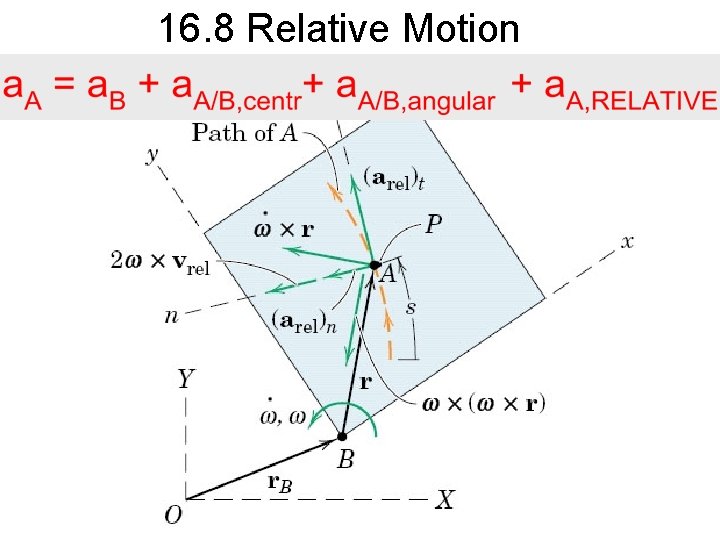
16. 8 Relative Motion

16. 8 Relative Motion From Ch. 12. 8 radial tangential

End of Review Chapters 14 and 16