Principles and Applications of NMR Spectroscopy Instructor Taihuang

Principles and Applications of NMR Spectroscopy Instructor: Tai-huang Huang (bmthh@ibms. sinica. edu. tw), (02) 2652 -3036 http: //www. nmr. sinica. edu. tw/~thh/lecture. html Time: Tuesday and/or Friday 2 -5 PM (9/21, 10/5, 10/8, 10/12, 10/15, 10/22, 10/26, 10/29, 11/2, 11/9, 11/12, 11/16, 11/19, 11/30, 12/7) Place: Rm. N 617, IBMS, Academia Sinica Textbooks: 1. Lecture by James Keeler on “Understanding NMR spectroscopy” (http: //www-keeler. ch. cam. ac. uk/lectures/) 2. Rules, G. S. and Hitchens, T. K. “Fundamentals of Protein NMR spectroscopy” 3. Cavanagh, Fairbrother, Palmer, and Skelton: “Protein NMR spectroscopy – Principles and practice” Academic press, 1996. 4. Selected review articles.

Curse Content This will be a comprehensive lecture course, focusing on modern high field NMR spectroscopy in solution, with applications to protein structure, dynamics and functional studies. Topics to be covered include: 1. Basic NMR theory, including quantum mechanical and vectorial descriptions of NMR spectroscopy. 2. Basic experimental aspects of NMR: NMR data acquisition and processing. 3. Product operator formalism analysis of pulse programs. 3. Spin dynamics: Coherent selection, phase cycling, gradient enhanced spectroscopy. 4. Heteronuclear multidimensional NMR spectroscopy. 5. Relaxation and protein dynamics. 6. Special topics: TROSY, RDC, PRE and reduced dimensionality etc. 7. Applications to protein NMR in solution.

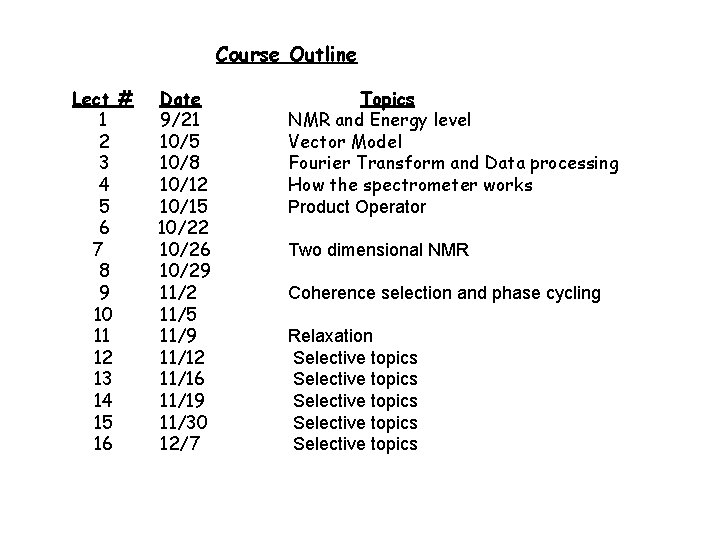
Course Outline Lect # 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Date 9/21 10/5 10/8 10/12 10/15 10/22 10/26 10/29 11/2 11/5 11/9 11/12 11/16 11/19 11/30 12/7 Topics NMR and Energy level Vector Model Fourier Transform and Data processing How the spectrometer works Product Operator Two dimensional NMR Coherence selection and phase cycling Relaxation Selective topics Selective topics

NMR Historic Review

2002 Nobel prize in Chemistry was awarded to Kurt Wuthrich NMR is a versatile tool and it has applications in wide varieties of subjects in addition to its chemical and biomedical applications, including material and quantum computing.

Isador I. Rabi 1944, Physics Richard R. Ernst 1992, Chemistry Edward M. Purcell 1952, Physics Kurt Wuthrich 2002, Chemistry Paul Lauterbur 2003, Medicine Felix Bloch 1952, Physics Peter Mansfield 2003, Medicine

CW NMR 40 MHz (1960)

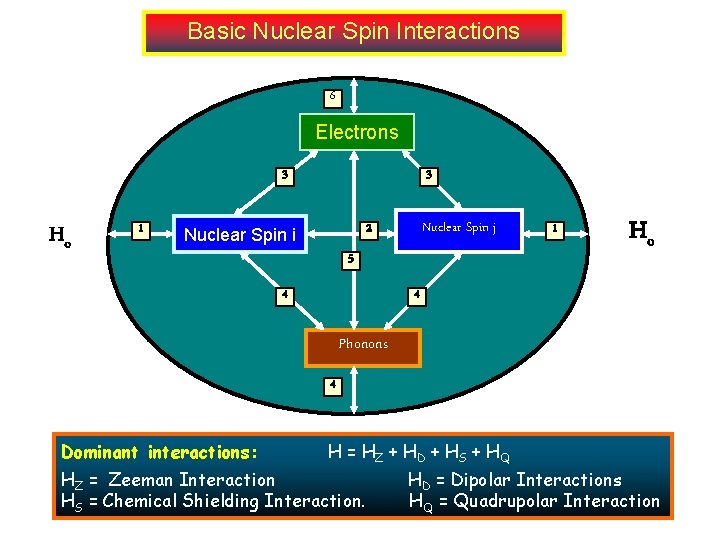
Basic Nuclear Spin Interactions 6 Electrons 3 Ho 1 3 Nuclear Spin j 2 Nuclear Spin i 5 4 1 Ho 4 Phonons 4 Dominant interactions: . H = HZ + HD + HS + HQ HZ = Zeeman Interaction HS = Chemical Shielding Interaction. HD = Dipolar Interactions HQ = Quadrupolar Interaction

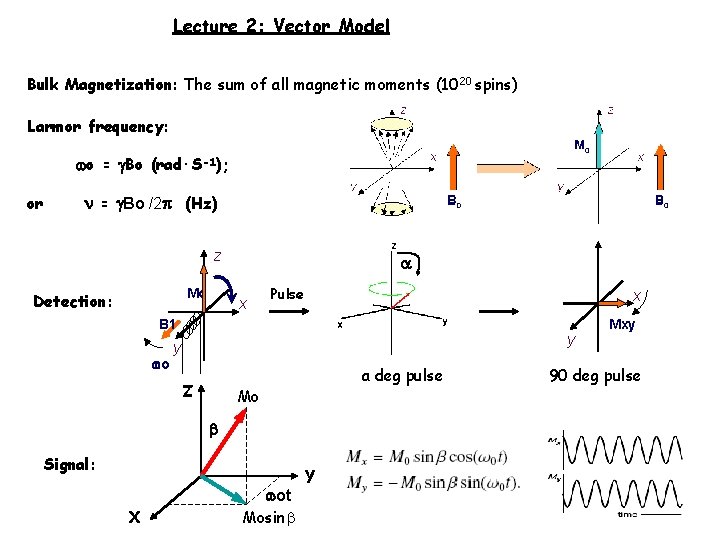
Lecture 2: Vector Model Bulk Magnetization: The sum of all magnetic moments (1020 spins) Larmor frequency: o = Bo (rad·S-1); or = Bo /2 (Hz) z Mo Detection: a x Pulse x B 1 o y y Z a deg pulse Mo Signal: X ot Mosin Y Mxy 90 deg pulse

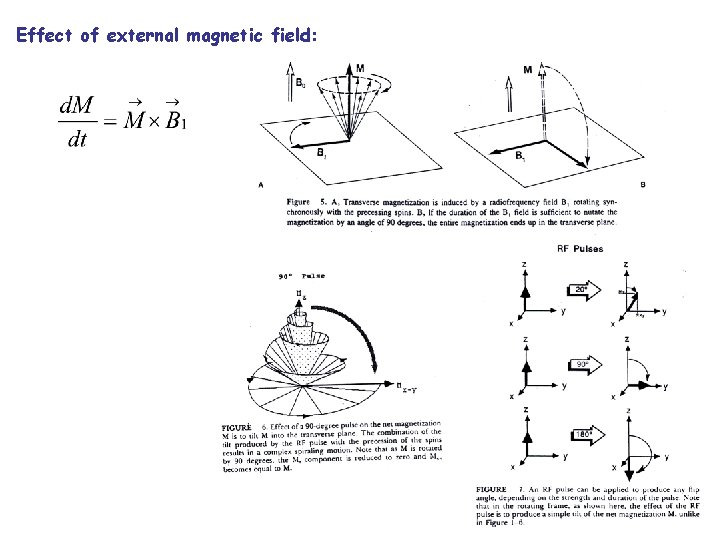
Effect of external magnetic field:

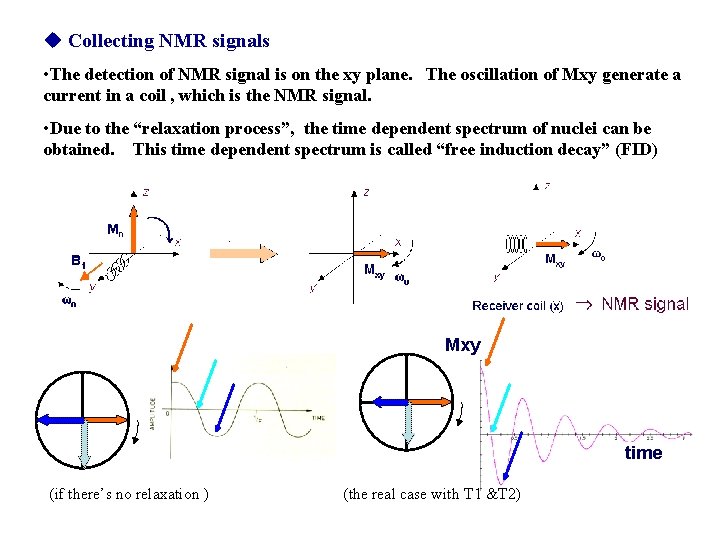
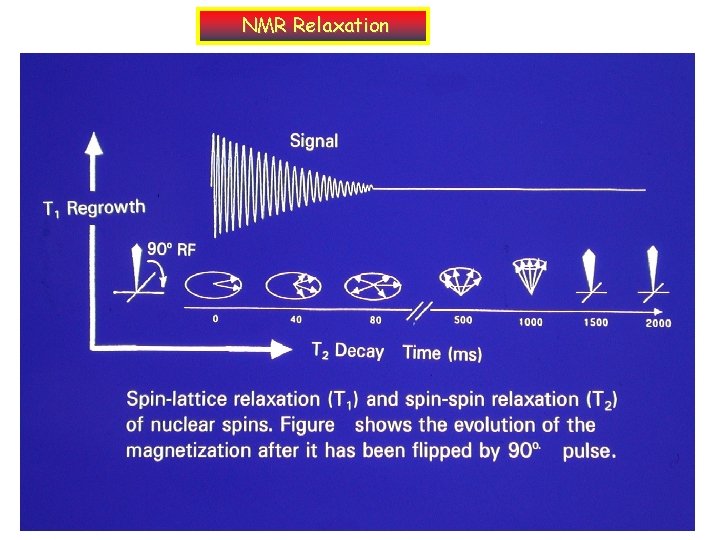
Collecting NMR signals • The detection of NMR signal is on the xy plane. The oscillation of Mxy generate a current in a coil , which is the NMR signal. • Due to the “relaxation process”, the time dependent spectrum of nuclei can be obtained. This time dependent spectrum is called “free induction decay” (FID) Mxy time (if there’s no relaxation ) (the real case with T 1 &T 2)

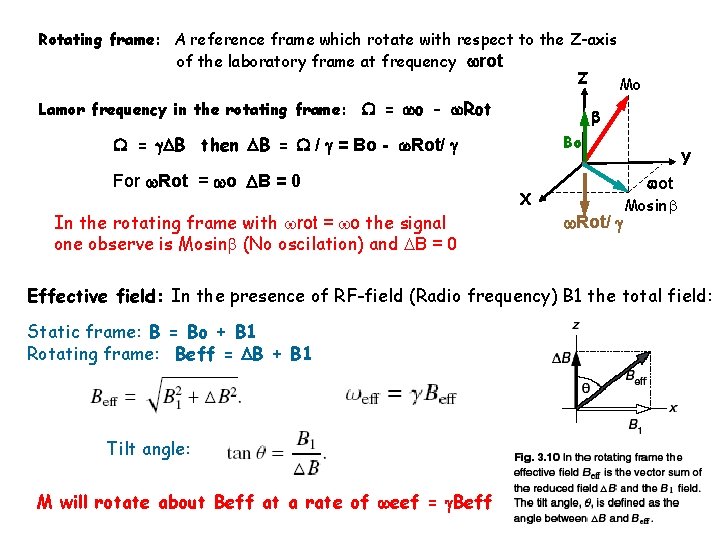
Rotating frame: A reference frame which rotate with respect to the Z-axis of the laboratory frame at frequency rot Z Mo Lamor frequency in the rotating frame: = o - Rot Bo = B then B = / = Bo - Rot/ For Rot = o B = 0 In the rotating frame with rot = o the signal one observe is Mosin (No oscilation) and B = 0 X Rot/ Y ot Mosin Effective field: In the presence of RF-field (Radio frequency) B 1 the total field: Static frame: B = Bo + B 1 Rotating frame: Beff = B + B 1 Tilt angle: M will rotate about Beff at a rate of eef = Beff

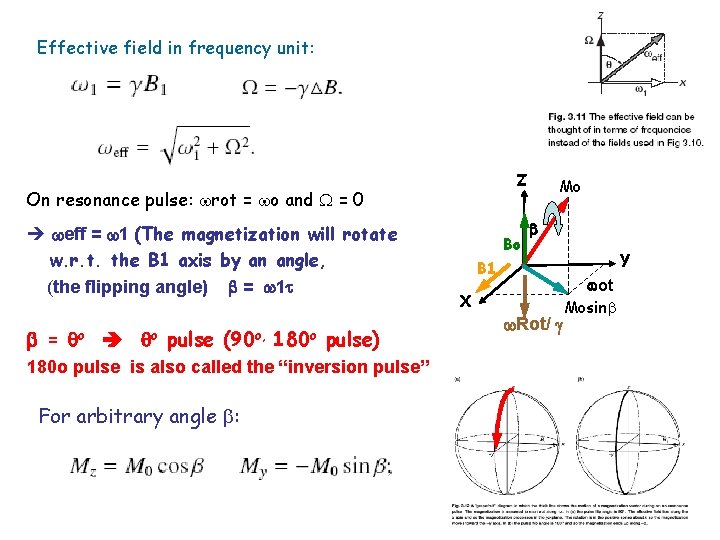
Effective field in frequency unit: Z On resonance pulse: rot = o and = 0 eff = 1 (The magnetization will rotate w. r. t. the B 1 axis by an angle, (the flipping angle) = 1 = o o pulse (90 o, 180 o pulse) 180 o pulse is also called the “inversion pulse” For arbitrary angle : Bo Mo B 1 X Rot/ Y ot Mosin

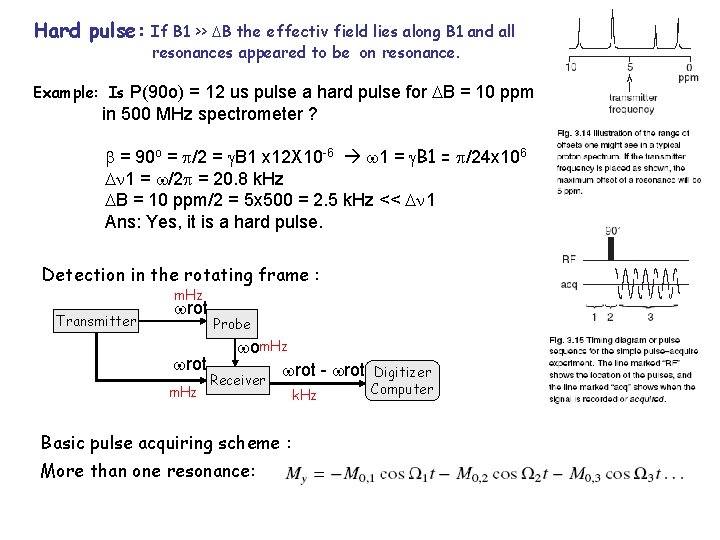
Hard pulse: If B 1 >> B the effectiv field lies along B 1 and all resonances appeared to be on resonance. Example: Is P(90 o) = 12 us pulse a hard pulse for B = 10 ppm in 500 MHz spectrometer ? = 90 o = /2 = B 1 x 12 X 10 -6 1 = B 1 = /24 x 106 1 = /2 = 20. 8 k. Hz B = 10 ppm/2 = 5 x 500 = 2. 5 k. Hz << 1 Ans: Yes, it is a hard pulse. Detection in the rotating frame : m. Hz Transmitter rot m. Hz Probe om. Hz rot - rot Receiver Basic pulse acquiring scheme : More than one resonance: k. Hz Digitizer Computer

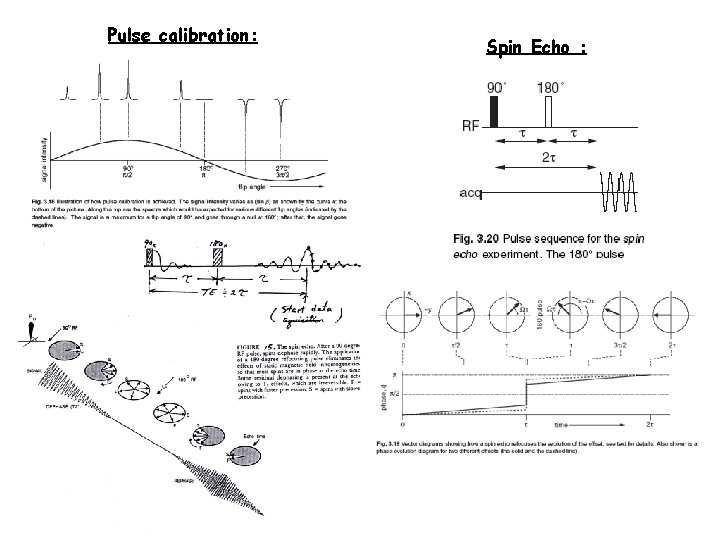
Pulse calibration: Spin Echo :

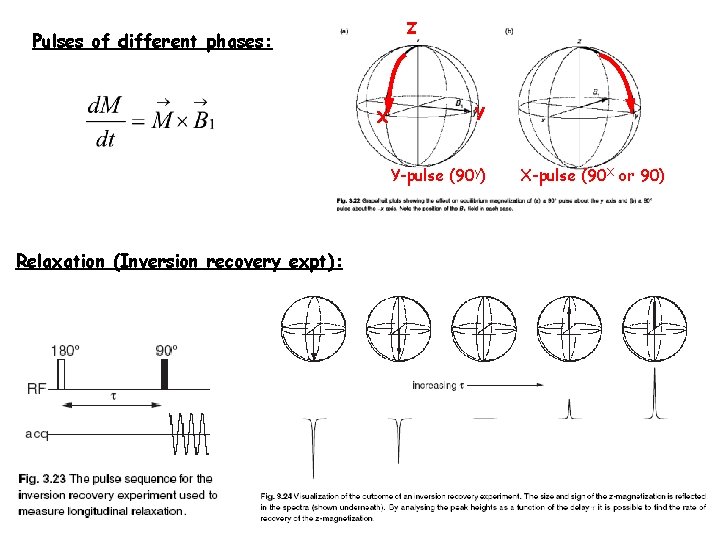
Z Pulses of different phases: X Y Y-pulse (90 y) Relaxation (Inversion recovery expt): X-pulse (90 X or 90)

NMR Relaxation

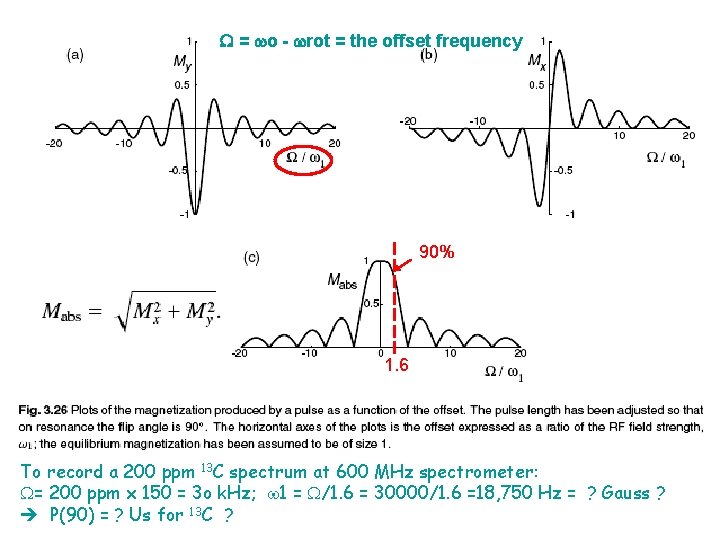
= o - rot = the offset frequency 90% 1. 6 To record a 200 ppm 13 C spectrum at 600 MHz spectrometer: = 200 ppm x 150 = 3 o k. Hz; 1 = /1. 6 = 30000/1. 6 =18, 750 Hz = ? Gauss ? P(90) = ? Us for 13 C ?

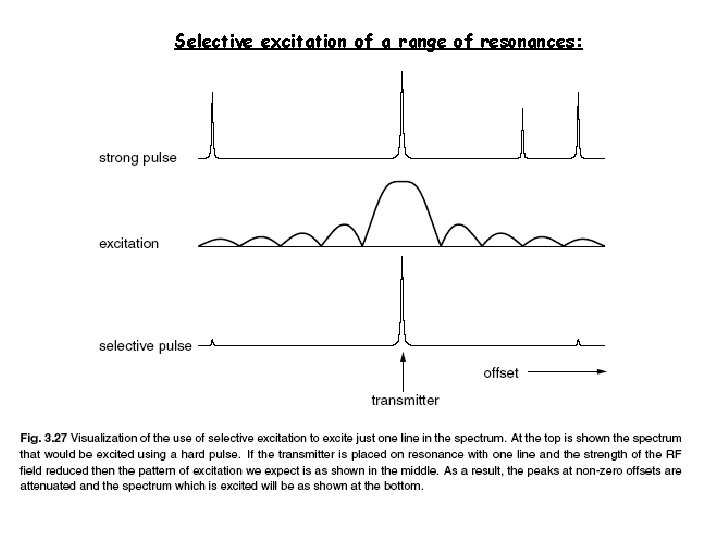
Selective excitation of a range of resonances:

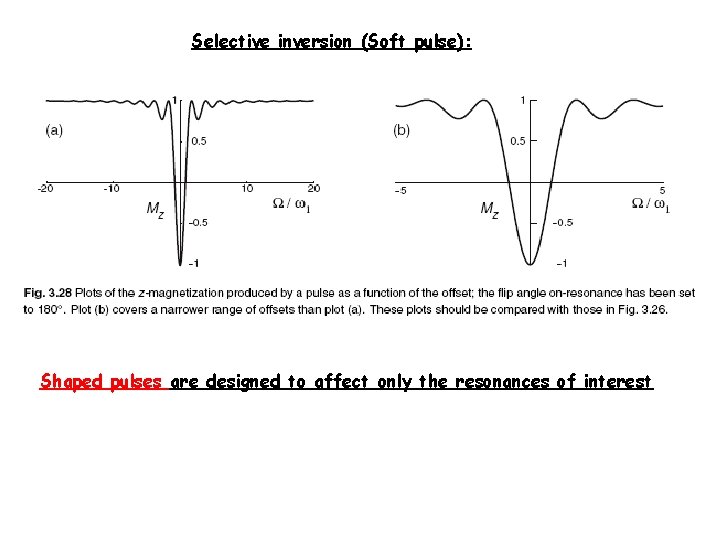
Selective inversion (Soft pulse): Shaped pulses are designed to affect only the resonances of interest