Principle of InclusionExclusion Principle of Inclusion and Exclusion

Principle of Inclusion-Exclusion

Principle of Inclusion and Exclusion • The Principle of Inclusion and Exclusion (PIE) is a counting technique that computes the number of elements that satisfy at least one of several properties while guaranteeing that elements satisfying more than one property are not counted twice.

Principle of Inclusion & Exclusion � � Section 3. 3 The above equation represents the principle of inclusion and exclusion for two sets A and B. The name comes from the fact that to calculate the elements in a union, we include the individual elements of A and B but subtract the elements common to A and B so that we don’t count them twice. This principle can be generalized to n sets. Principle of Inclusion & Exclusion; Pigeonhole Principle 4

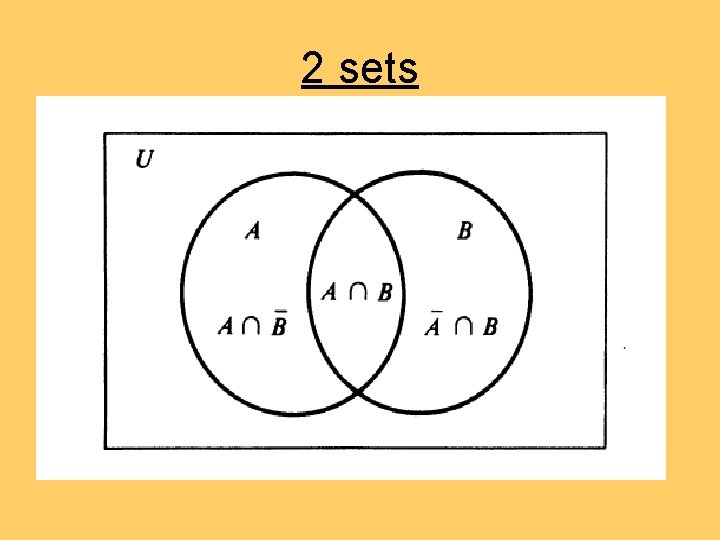
Inclusion-Exclusion U A A B It’s simply a matter of not over-counting the blue area in the intersection.

2 sets

Problem 1

• If F is faculty who speak French and R is the faculty who speak Russian, then given that • n(F) = |F| = 200 • n(R) = |R|= 50 • n (F∩R) = | F∩R | = 20 and we need to find |F U R| • Then by the PIE we have | F∩R | = |F| + |R| - |F U R| • Thus |F U R| = 200+50 -20=230

Problem 2

• Total number of committees possible is C(10, 5) = 252 ways • Let A be the set of committees that include Professor-A and B be the set of committees that include Professor-B. Then • n(A) = • C (9, 4)=126 • n(B) = • C (9, 4)=126 • n(A ∩ B) = • C(8, 3) = 56…thus by inclusion and exclusion principle • n(A U B) = 126 + 126 – 56 = 196

Example on Inclusion/Exclusion Rule (2 sets) • Question: How many integers from 1 through 100 are multiples of 3 or multiples of 7 ? • Solution: Let A=the set of integers from 1 through 100 which are multiples of 3; B = the set of integers from 1 through 100 which are multiples of 7. Then we want to find n(A U B). First note that A ∩ B is the set of integers from 1 through 100 which are multiples of 21. n(A U B) = n(A) + n(B) - n(A ∩ B) (by incl. /excl. rule)

• n(AUB) = n(A) + n(B) - n(A ∩ B) (by incl. /excl. rule) • = 33 + 14 – 4 = 43 (by counting the elements From 1 to 100, every third integer is a multiple of 3, each of this multiple can be represented as 3 p, for any integer p from 1 through 33, Hence |A| = 33. Similarly for multiples of 7, each multiple of 7 is of the form 7 q for some integer q from 1 through 14. Hence, we have |B| = 14. ) and the multiple of 21… n(A ∩ B) = 4

Example: Inclusion and Exclusion Principle � Example 1: How many integers from 1 to 1000 are either multiples of 3 or multiples of 5? � � � To use the inclusion/exclusion principle to obtain |A U B|, we need |A|, |B| and |A ∩ B|. � � Section 3. 3 Let us assume that A = set of all integers from 1 to 1000 that are multiples of 3. Let us assume that B = set of all integers from 1 to 1000 that are multiples of 5. A U B = The set of all integers from 1 to 1000 that are multiples of either 3 or 5. A ∩ B = The set of all integers that are both multiples of 3 and 5, which also is the set of integers that are multiples of 15. From 1 to 1000, every third integer is a multiple of 3, each of this multiple can be represented as 3 p, for any integer p from 1 through 333, Hence |A| = 333. Similarly for multiples of 5, each multiple of 5 is of the form 5 q for some integer q from 1 through 200. Hence, we have |B| = 200. Principle of Inclusion & Exclusion; Pigeonhole Principle 13

Example: Inclusion/exclusion principle for 3 sets To determine the number of multiples of 15 from 1 through 1000, each multiple of 15 is of the form 15 r for some integer r from 1 through 66. Hence, |A ∩ B| = 66. From the principle, we have the number of integers either multiples of 3 or multiples of 5 from 1 to 1000 given by |A U B| = 333 + 200 – 66 = 467. Section 3. 3 Principle of Inclusion & Exclusion; Pigeonhole Principle 14

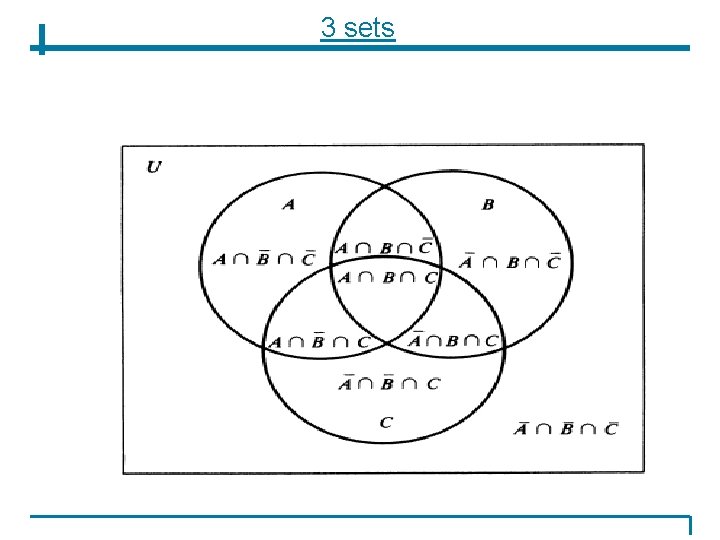
3 sets

Problem 3

� � � � Section 3. 3 Let F be the set of faculty who speak French, R be the set of faculty who speak Russian, and S be the set of faculty that speak Spanish. Thus we have |F | = 200, | R | = 50, |S|= 100 |F ∩ R | = 20 |F ∩ S | = 60 |R∩ S | = 35 |F ∩ R∩ S | = 10 Thus | F U R U S | = 200 + 50+ 100 - 20 -60 -35 + 10 = 245. Principle of Inclusion & Exclusion; Pigeonhole Principle 17

Example 2: • In a class of students undergoing a computer course the following were observed. – Out of a total of 50 students: 30 know Pascal, 18 know Fortran, 26 know COBOL, 9 know both Pascal and Fortran, 16 know both Pascal and COBOL, 8 know both Fortran and COBOL, 47 know at least one of the three languages. • From this we have to determine – a. How many students know none of these languages? – b. How many students know all three languages?

Example: Inclusion/exclusion principle for 3 sets a. We know that 47 students know at least one of the three languages in the class of 50. The number of students who do not know any of three languages is given by the difference between the number of students in class and the number of students who know at least one language. • b. Students know all three languages, so we need to find |A B C|. § � � � Section 3. 3 Hence, the students who know none of these languages = 50 – 47 = 3. A = All the students who know Pascal in class. B = All the students who know COBOL in the class. C = All the students who know FORTRAN in class. We have to derive the inclusion/exclusion formula for three sets |A B C| = |A (B C)| = |A| + |B C| - |A (B C)| Principle of Inclusion & Exclusion; Pigeonhole Principle 19

Example: Inclusion/exclusion principle for 3 sets � � � Section 3. 3 |A B C| = |A (B C)| = |A| + |B C| - |A (B C)| = |A| + |B| + |C| - |B C| - |(A B) (A C)| = |A| + |B| + |C| - |B C| - (|A B| + |A C| - |A B C|) = |A| + |B| + |C| - |B C| - |A B| - |A C| + |A B C| Given in the problem are the following: |B C| = 8 |A B| = 9 |A C| =16 |A B C| = 50 Hence, using the above formula, we have 47 = 30 + 26 + 18 -9 -16 -8 + |A B C| Hence, |A B C| = 6 Principle of Inclusion & Exclusion; Pigeonhole Principle 20

Example on Inclusion/Exclusion Rule (3 sets) • 3 headache drugs – A, B, and C – were tested on 40 subjects. The results of tests: 23 reported relief from drug A; 18 reported relief from drug B; 31 reported relief from drug C; 11 reported relief from both drugs A and B; 19 reported relief from both drugs A and C; 14 reported relief from both drugs B and C; 37 reported relief from at least one of the drugs. Questions: 1) How many people got relief from none of the drugs? 2) How many people got relief from all 3 drugs? 3) How many people got relief from A only?

Example on Inclusion/Exclusion Rule (3 sets) S C A B We are given: n(A)=23, n(B)=18, n(C)=31, n(A B)=11, n(A C)=19, n(B C)=14 , n(S)=40, n(A B C)=37 Q 1) How many people got relief from none of the drugs? By difference rule, n((A B C)c ) = n(S) – n(A B C) = 40 - 37 = 3

Example on Inclusion/Exclusion Rule (3 sets) Q 2) How many people got relief from all 3 drugs? By inclusion/exclusion rule: n(A B C) = n(A B C) - n(A) - n(B) - n(C) + n(A B) + n(A C) + n(B C) = 37 – 23 – 18 – 31 + 19 + 14 = 9 Q 3) How many people got relief from A only? n(A – (B C)) (by inclusion/exclusion rule) = n(A) – n(A B) - n(A C) + n(A B C) = 23 – 11 – 19 + 9 = 2

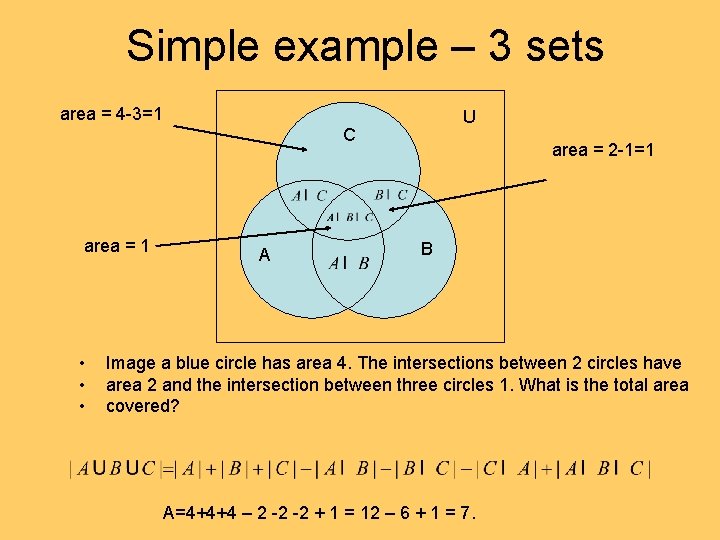
Simple example – 3 sets area = 4 -3=1 U C area = 1 • • • A area = 2 -1=1 B Image a blue circle has area 4. The intersections between 2 circles have area 2 and the intersection between three circles 1. What is the total area covered? A=4+4+4 – 2 -2 -2 + 1 = 12 – 6 + 1 = 7.

PIE De. Morgon’s laws

Cont…

Solution

exercises

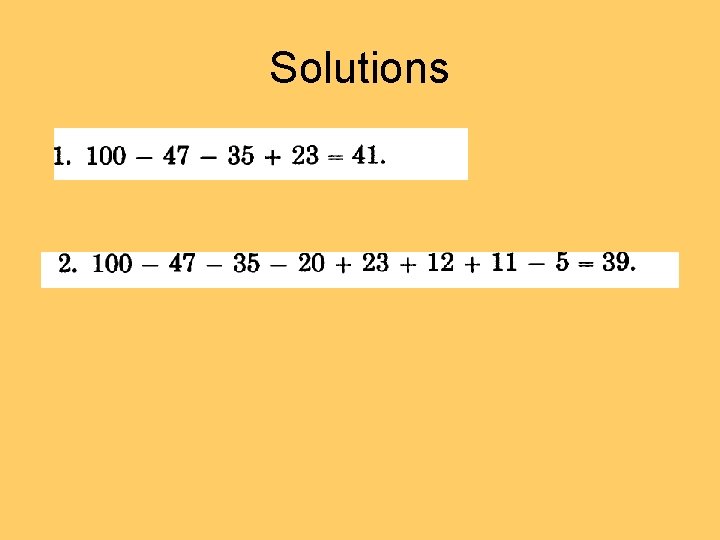
Solutions

Examples Compute the number of solutions to x 1+x 2+x 3=11 where x 1, x 2, x 3 non-negative integers and x 1 <=3, x 2<=4, x 4<=6. P 1: x 1 > 3 P 2: x 2 > 4 P 3: x 3 > 6 The solution must have non of the properties P 1, P 2, P 3. The solution of a problem x 1+x 2+x 3=11 with constraints x 1 > 3 is solved as follows: 7 more balls 4 balls in basket x 1 already. x 1 x 2 x 3 Total number of ways: C(7+3 -1, 7)=36 Therefore: N-N(P 1)-N(P 2)-N(P 3)+N(P 1, P 2)+N(P 2, P 3)+N(P 1, P 3)-N(P 1, P 2, P 3) = C(11+3 -1, 11) – C(7+3 -1, 7) – C(6+3 -1, 6) – C(4+3 -1, 4) + … – 0.