Principe de dure Dure de Macauley est la

Principe de durée Durée (de Macauley) est la période au terme de laquelle la rentabilité espérée d’une obligation n’est pas affectée par les variations de taux d’intérêt; moment où s’équilibrent : • La hausse (ou la baisse) de la valeur future de l’obligation provoquée par une variation du cours de l’obligation • La baisse (ou la hausse) de la valeur future de l’obligation provoquée par le réinvestissement des coupons au nouveau taux d’intérêt Mesure de l’exposition au risque de taux d’intérêt d’une obligation (risque systématique) où wt = CFt (1+y)-t / P 0 Poids accordé d’un cash flow au temps t; proportion de ce cash flow, actualisé au taux de rendement à l’échéance, par rapport au prix initial de l’obligation (P 0) t Temps à écouler pour recevoir le cash flow Niveau d’exposition actuel Analyse quantitative Implantation Conclusion

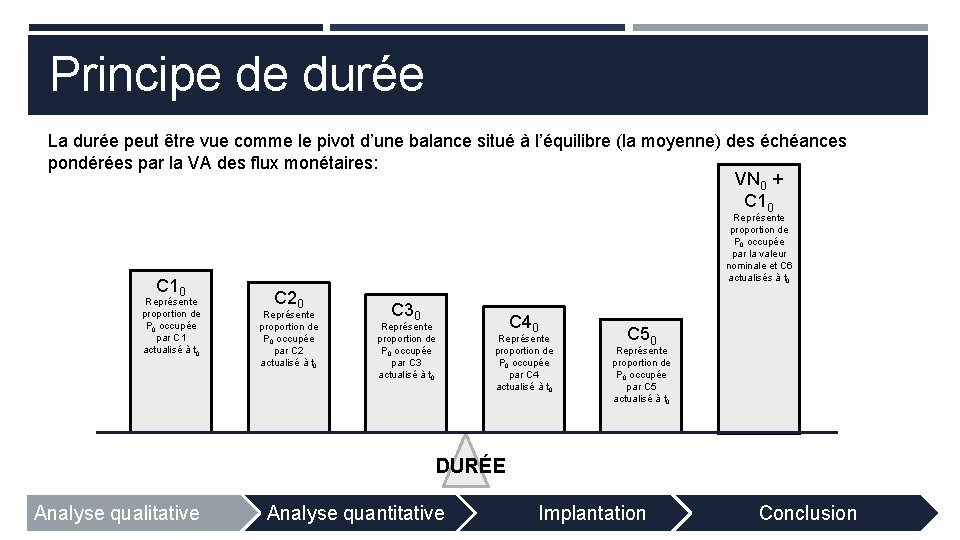
Principe de durée La durée peut être vue comme le pivot d’une balance situé à l’équilibre (la moyenne) des échéances pondérées par la VA des flux monétaires: VN 0 + C 10 Représente proportion de P 0 occupée par C 1 actualisé à t 0 Représente proportion de P 0 occupée par la valeur nominale et C 6 actualisés à t 0 C 20 Représente proportion de P 0 occupée par C 2 actualisé à t 0 C 30 C 40 Représente proportion de P 0 occupée par C 3 actualisé à t 0 Représente proportion de P 0 occupée par C 4 actualisé à t 0 C 50 Représente proportion de P 0 occupée par C 5 actualisé à t 0 DURÉE Analyse qualitative Analyse quantitative Implantation Conclusion

Principe de durée Plus la durée est grande, plus l’exposition au risque de taux d’intérêt est élevée Une hausse de la durée est entraînée par: • baisse du taux de coupon • hausse de l’échéance • baisse du taux de rendement à l’échéance Plus la durée est faible, plus l’exposition au risque de taux d’intérêt est faible Une baisse de la durée est entraînée par: • hausse du taux de coupon • baisse de l’échéance • hausse du taux de rendement à l’échéance Analyse qualitative Analyse quantitative Implantation Conclusion

Principe de durée Durée modifiée s’obtient à partir de la durée de Macauley Mesure plus précise de la variation du prix d’une obligation qui suit une variation de 100 BPS du taux d’intérêt Dm = D / (1 + y) → Prix ($) ∆P 0 = P 0 x - Dm x ∆y exprimé en % de P 0 Le graphique expose une des faiblesses de la durée comme mesure du risque; 1 - Elle n’est plus valable lorsque les variations du taux d’intérêt sont grandes, car elle ne tient pas compte de la convexité de la relation prix-taux de rendement à l’échéance. ∆P 0 /∆y Dm y (%) Analyse qualitative Limites: Analyse quantitative D’autres points faibles existent… Implantation Conclusion

Principe de durée Limites (suite): 2 - Le concept de durée repose sur l’hypothèse d’une structure à terme des taux d’intérêt plate, et des variations parallèles de cette structure dans le temps. 3 - Finalement, ce n’est pas une mesure appropriée concernant des obligations non-standards comportant des clauses optionnelles comme de rachat ou de convertibilité. La durée effective servira d’approximation de la durée pour ce type d’obligation. Durée effective = P- - P+ / P 0 (y+ - y-) Où P- : prix si les taux baissent P+ : prix si les taux montent y- : taux si les taux baissent y+ : taux si les taux augmentent Analyse qualitative Analyse quantitative Implantation Conclusion

Principe de convexité Pour faire en sorte que la durée modifiée soit applicable à de grandes variations de taux d’intérêt, il est nécessaire de considérer la convexité Analyse qualitative Analyse quantitative Implantation Conclusion

Durée modifiée et convexité La convexité vient corriger l’estimation de la variation du prix fait par la durée; Ø La durée modifiée sous-estime les variations du prix suite aux variations du taux d’intérêt Ø La convexité surestime les variations du prix Prix ($) Variation du prix (corrigée) ∆P/P 0 = -Dm x ∆y + ½ convexité x ∆y 2 ∆P = P 0 [ -Dm x ∆y + ½ convexité x ∆y 2 ] Pour une même variation de y, le prix varie davantage si on se situe à un niveau initial plus faible des taux (en %) (en $) y (%) Si les taux d’intérêt sont initialement élevés, moins une variation de ces derniers affectera le prix. Si les taux d’intérêt sont initialement faibles, plus une variation de ces derniers affectera le prix. Analyse qualitative Analyse quantitative Implantation Conclusion

Principe d’immunisation par la durée Repose sur le fait, qu’à la durée, la perte en capital causée par la hausse du taux d’intérêt est compensée par la hausse du rendement des coupons réinvestis Immunisation par la durée Investir dans les obligations dont la durée concorde avec notre horizon de placement; on s’assure de réaliser le rendement promis au moment de l’achat Limites: • Immunisation imparfaite si grande variation des taux • Durée doit toujours être égale à l’horizon de placement (la durée ne diminue pas nécessairement au même rythme que le temps passe, donc stratégie dynamique) • Si le taux d’intérêt change en cours de route, il faut modifier la stratégie d’immunisation • Suppose STTI horizontale et mouvements parallèles Analyse qualitative Analyse quantitative Implantation Conclusion