Principal Stresses and Strain and Theories of Failure

Principal Stresses and Strain and Theories of Failure Strength of Materials Prof. A. S. PATIL Department of Mechanical Engineering Sinhgad Academy of Engineering, Pune Strength of Materials 1

3. Maximum Distortion Energy Theory (von Mises Criterion) • Failure occurs when the distortional energy associated with the principal stresses equals or exceeds the distortional energy corresponding to that for the yield strength of the material in uniaxial tension. • ductile material • based on a limiting energy of distortion (shear strains) • 0. 5 ( (σ1 - σ2)2 + (σ2 - σ3)2 + (σ3 - σ1)2) < σyp 2 Strength of Materials 2

Maximum Distortion Energy Theory (von Mises Criterion) For the three principal stresses; Strength of Materials 3

After taking out the hydrostatic stress (save=(s 1+s 2+s 3)/3) Now substitute s 1, s 2 and s 3 with For plane stress; in an uniaxial tension test. Strength of Materials 4

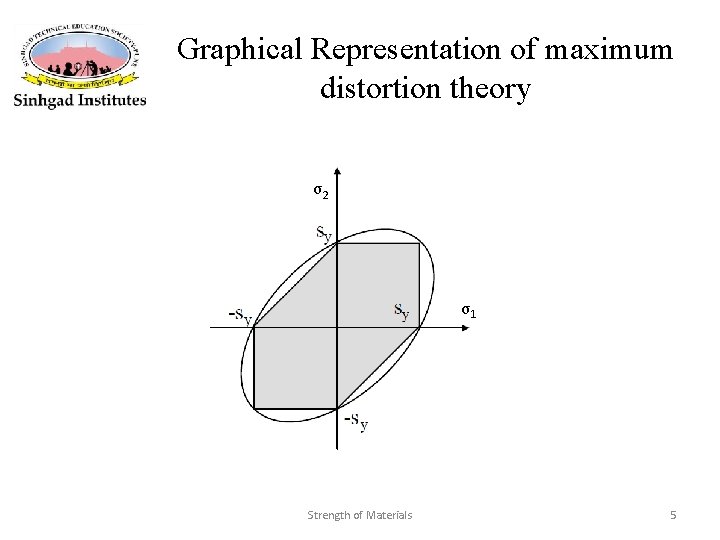
Graphical Representation of maximum distortion theory σ2 σ1 Strength of Materials 5

4. Maximum Strain Theory • Strength of Materials 6

Maximum Strain Theory • Strength of Materials 7

NUMERICAL 1. Stresses induced at a critical point in a machine component made of steel are as follows: σ1 = 120 Mpa , σ2 = - 40 Mpa , τxy = 80 N/mm 2 Calculate the factor of safety by: 1) Max. Shear Stress Theory 2) Max. Normal Stress Theory 3) Max. Distortion Energy Theory Take Syt = 380 N/mm 2 Strength of Materials 8

• Given: σx = 120 Mpa , σy = - 40 Mpa , τxy = 80 N/mm 2 Syt = 380 N/mm 2 Solution : Principal Stress Strength of Materials 9

• σ1 = 153. 13 N/mm 2 , σ2 = -73. 14 N/mm 2 • Maximum shear stress = 113. 135 N/mm 2 Strength of Materials 10

• Factor of Safety by: 1) Maximum Shear stress theory: = 1. 68 2) Maximum Normal stress theory: = 2. 48 Strength of Materials 11

3) Maximum Distortion Energy Theory: - FOS = 1. 9 Strength of Materials 12

2. A bolt is under an axial pull of 24 k. N together with a transverse shear force of 5 k. N. Calculate the diameter if bolt using i) Max. principle stress theory ii) Max. shear stress theory iii) Strain energy theory Take, elastic limit of bolt material as 250 MPa and µ = 0. 3. Factor of safety is 2. 5 Strength of Materials 13

Given: d = diameter of the bolt in mm P = 24 k. N , Shear force S = 5 k. N σy = 250 N/mm 2 FOS = 2. 5 µ = 0. 3 Solution: - Strength of Materials 14

• Strength of Materials 15

• Strength of Materials 16

Examples to solve 1. A solid circular shaft subjected to bending moment of 60 k. Nm and a torque of 15 k. Nm. Design the diameter of the shaft using. i) Max. principle stress theory ii) Max. shear stress theory iii) Max. strain energy theory Take µ = 0. 28, yield strength of shaft is 225 MPa and factor of safety = 2. 5 2. A square pin is required to resist a pull of 40 k. N. Derive a suitable section according to strain energy theory. Maximum tensile stress is 350 MPA and Poisson’s ratio is 0. 3. Take factor of safety of 2. 5 Strength of Materials 17

Numerical • A shaft is supported in a bearing 4 m apart and transmits 60 k. W at 160 rpm. At 1. 2 m from one bearing the shaft carries a pulley transmitting a load of 50 k. N on the shaft. Find the suitable diameter for the shaft for each of the following cases. i) Maximum direct stress shall not exceed 120 N/mm 2 ii) Maximum shear stress shall not exceed 60 N/mm 2 Ans: - i) D= 133. 2 mm ii) D= 134. 5 mm Strength of Materials 18