Principal Component Analysis of Flow Subrata Pal Tata

Principal Component Analysis of Flow Subrata Pal Tata Institute of Fundamental Research, Mumbai, India Outline Ø Introduction and standard methods to determine anisotropic flow Ø Principal Component Analysis (PCA) Ø Application to 2 -particle correlation matrix Ø Results in AMPT (η, p. T) and ALICE (p. T) Ø Conclusions

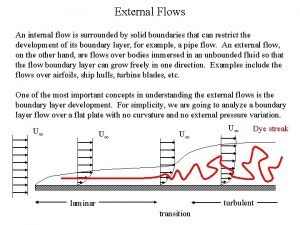
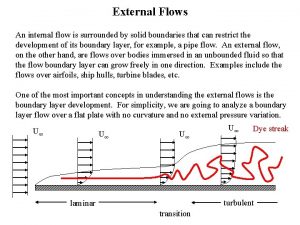
Flow analysis in heavy ion collision 2

Anisotropic flow vn Origin of elliptic flow v 2: spatial anisotropy and re-interaction Ollitrault PRD 46 (1992) 229 Harmonic flow vector relates to various moments of initial spatial anisotropy (eccentricities) of nucleons/partons n = magnitude (eccenticities) Φn = phase (participant-plane angle) Eby. E initial distribution: p( n, m, …. , Φn, m, …) Alver & Roland, PRC 81(2010) 054905 Flow observable Origin of triangular flow v 3: fluctuations in the position of participant nucleons Collective/Hydro expansion ( , Eo. S, /s, …) 3

Standard methods to estimate vn Event Plane method Ollitrault PRD 46 (1992) 229 vn are Fourier coeffecients in φ distrn of particles wrt reaction plane Event Plane angle: Entire Flow vector can be expressed in a complex plane: vn(p. T, ) = magnitude (anisotropic flow) n(p. T, ) = phase (event-plane angle along minor axis) NB: flow fluctuations can modify vn and Ψn 4

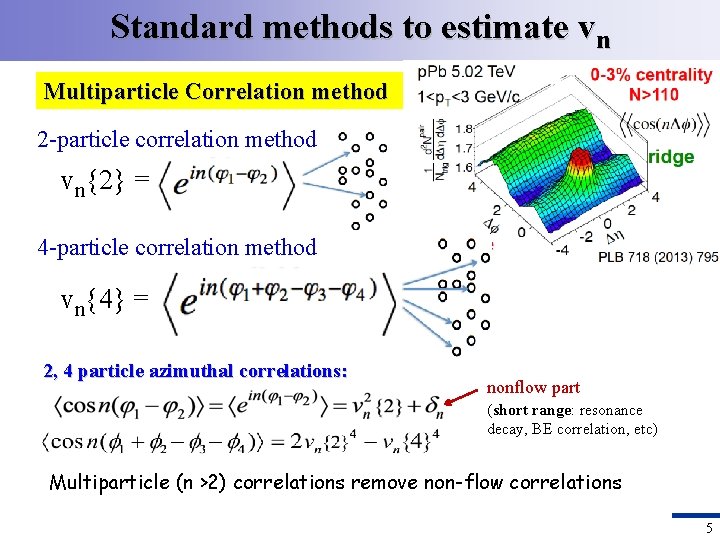
Standard methods to estimate vn Multiparticle Correlation method 2 -particle correlation method vn{2} = 4 -particle correlation method vn{4} = 2, 4 particle azimuthal correlations: nonflow part (short range: resonance decay, BE correlation, etc) Multiparticle (n >2) correlations remove non-flow correlations 5

Principal Component Analysis (PCA) 6

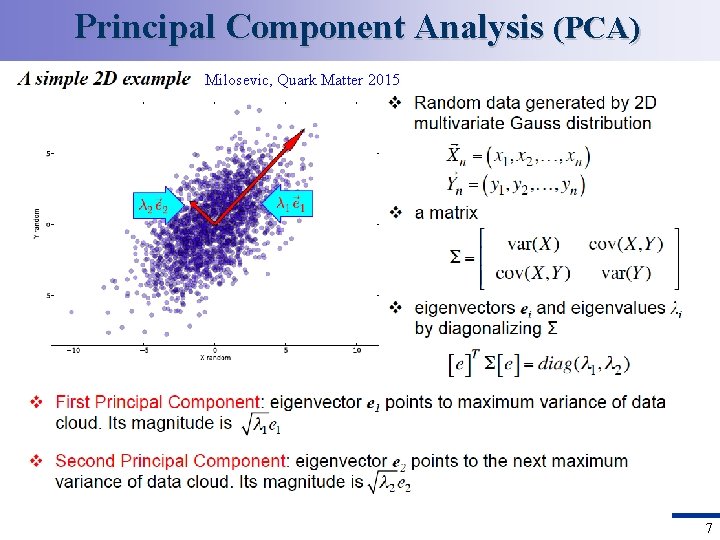
Principal Component Analysis (PCA) Milosevic, Quark Matter 2015 7

Flow picture Fourier coeff Vn(p) Vn(p. T, ) Note: Bhalerao, Ollitrault, SP, Teaney: PRL 114 (2015) 152301 8

Covariance matrix Vn(p) I. e. one component (k=1) exits corresp. to usual anisotropic flow. Flow fluctuations break factorization and k ≤ Nb (= # of bins in p) 9

Method to calculate flow in PCA subtracts self-correl singles out fluc. 10

Method to calculate flow in PCA 11

A Multi. Phase Transport model (AMPT) Inclusive hadron distribution – calculable in p. QCD ΔE Energy loss Lin, Ko, Li, Zhang, SP, PRC 72 (2005) 064901 SP, Bleicher, PLB 709 (2012) 82 12

AMPT with updated HIJING 2. 0 • GRV parametrization of parton distribution function Deng, Wang, Xu, PLB 701 (2011) 133 PDF in nucleus: Impact parameter dependent shadowing sq = 0. 1 (fixed) from deep-inelastic- scattering data off nuclear targets. sg fitted to centrality dependence of measured d. Nch/dy in A+A collision.

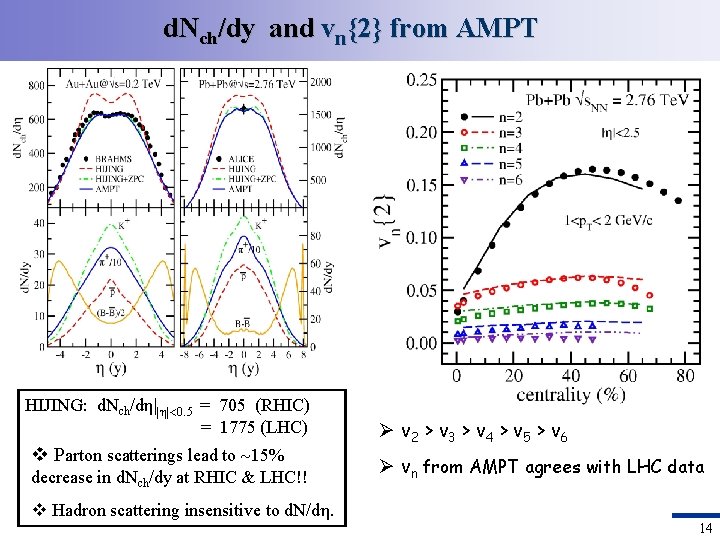
d. Nch/dy and vn{2} from AMPT HIJING: d. Nch/dη||η| 0. 5 = 705 (RHIC) = 1775 (LHC) v Parton scatterings lead to 15% decrease in d. Nch/dy at RHIC & LHC!! Ø v 2 > v 3 > v 4 > v 5 > v 6 Ø vn from AMPT agrees with LHC data v Hadron scattering insensitive to d. N/dη. 14

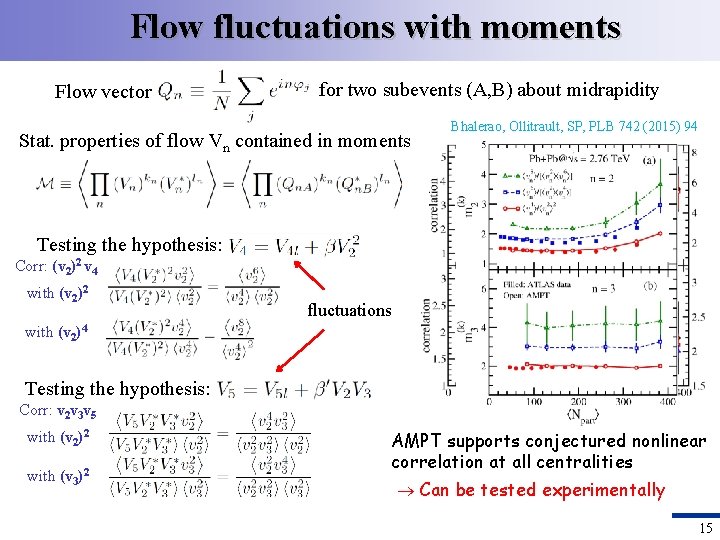
Flow fluctuations with moments Flow vector for two subevents (A, B) about midrapidity Stat. properties of flow Vn contained in moments Bhalerao, Ollitrault, SP, PLB 742 (2015) 94 Testing the hypothesis: Corr: (v 2)2 v 4 with (v 2)2 fluctuations with (v 2)4 Testing the hypothesis: Corr: v 2 v 3 v 5 with (v 2)2 with (v 3)2 AMPT supports conjectured nonlinear correlation at all centralities Can be tested experimentally 15

Event plane correlations p( n, m, . . . ) EP correlators involve 3 -particles higher order correlations vn measured with single EP: Res n Correlations from multi-particles: {EP} {SP} Res( 1) Res(2 2) … Res(kn n) k 1+2 k 2+…+nkn=0 Experimental analysis: (i) each EP in different -window; (ii) windows pairwise separated by gaps decrease statistics 2 -subevent method for EP correlators Bhalerao, Ollitrault, SP, PRC 88 (2013) 024909 Consider 2 subevents (A, B) separated by a -gap. Construct flow vector for each subevent: EP method: Scalar product method: Resolution dependent Well-defined flow observable 16

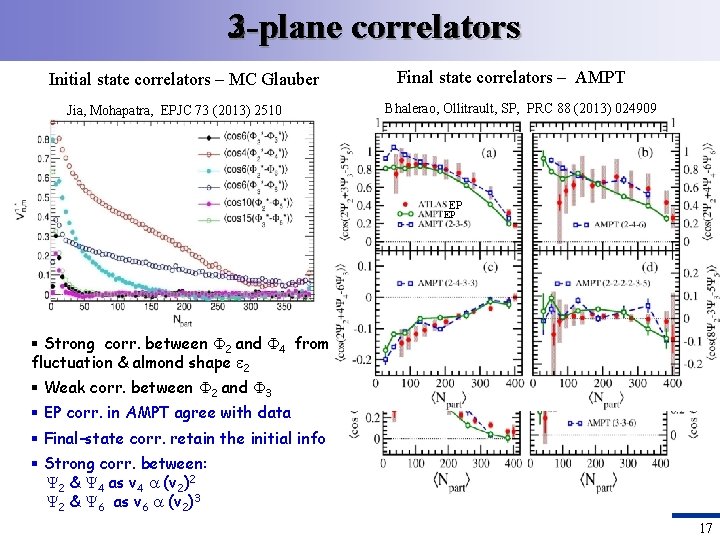
3 -plane 2 -plane correlators Initial state correlators – MC Glauber Jia, Mohapatra, EPJC 73 (2013) 2510 Final state correlators – AMPT Bhalerao, Ollitrault, SP, PRC 88 (2013) 024909 EP EP § Strong corr. between 2 and 4 from fluctuation & almond shape 2 § Weak corr. between 2 and 3 § EP corr. in AMPT agree with data § Final-state corr. retain the initial info § Strong corr. between: 2 & 4 as v 4 (v 2)2 2 & 6 as v 6 (v 2)3 17

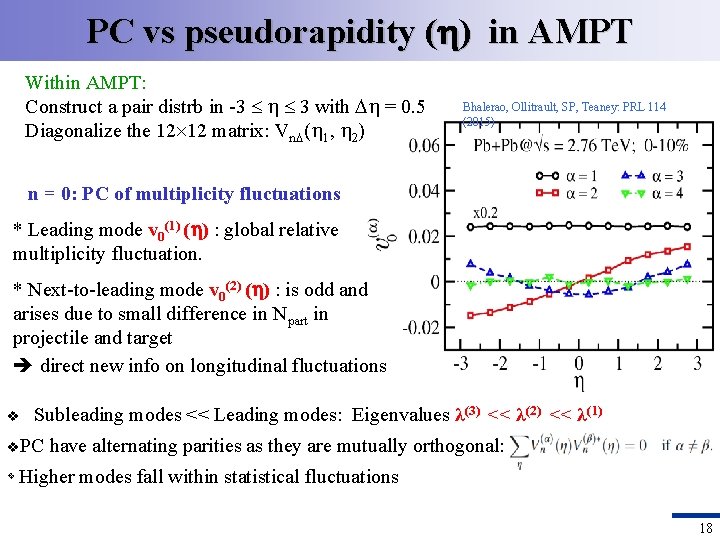
PC vs pseudorapidity ( ) in AMPT Within AMPT: Construct a pair distrb in -3 3 with = 0. 5 Diagonalize the 12 12 matrix: Vn ( 1, 2). Bhalerao, Ollitrault, SP, Teaney: PRL 114 (2015) n = 0: PC of multiplicity fluctuations * Leading mode v 0(1) ( ) : global relative multiplicity fluctuation. * Next-to-leading mode v 0(2) ( ) : is odd and arises due to small difference in Npart in projectile and target direct new info on longitudinal fluctuations v Subleading modes << Leading modes: Eigenvalues λ(3) << λ(2) << λ(1) v. PC v have alternating parities as they are mutually orthogonal: Higher modes fall within statistical fluctuations 18

PC vs in AMPT PC: Elliptic (n = 2), Triangular (n=3) flow fluctuations * Leading modes v 2(1), v 3(1) : usual elliptic and triangular flow that weakly depend on . v Subleading modes << Leading modes. v Next-to-leading mode v 2, 3(2) ( ) : torqued flow Emission profiles of forward (f+) and backward (f-) moving wounded nucleons in Eby. E basis causes a torque of the principal axis (or participant plane). Bozek, Broniowski, Moreira, PRC 83 (2011) 034911 Direction of principal axis in transverse plane rotates as rapidity increases. The initial torque is converted into torqued flow v 2(2) ( ) and v 3(2) ( ). Elliptic Triangular 19

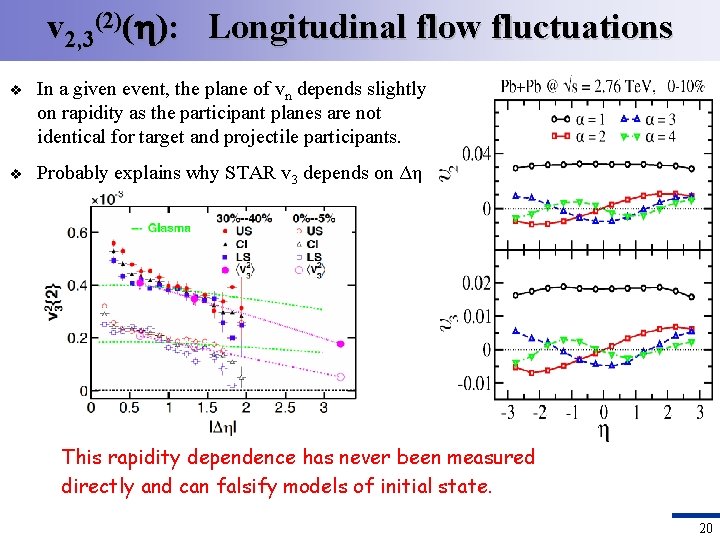
v 2, 3(2)( ): Longitudinal flow fluctuations v In a given event, the plane of vn depends slightly on rapidity as the participant planes are not identical for target and projectile participants. v Probably explains why STAR v 3 depends on Δη This rapidity dependence has never been measured directly and can falsify models of initial state. 20

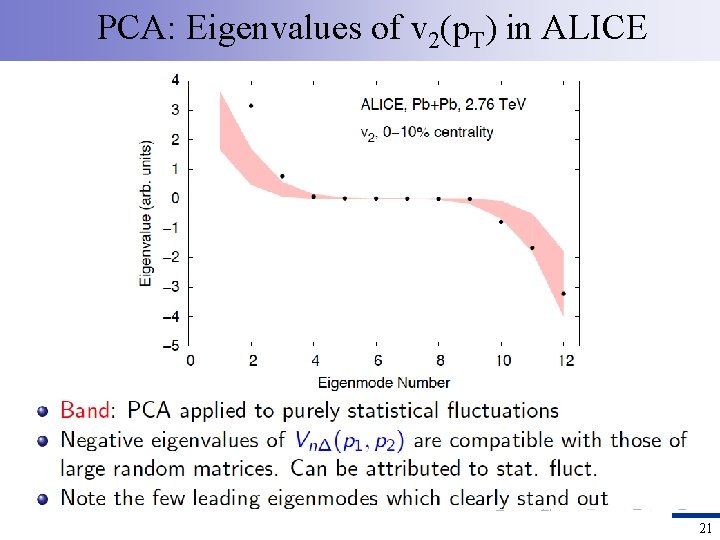
PCA: Eigenvalues of v 2(p. T) in ALICE 21

PCA: Eigenvalues of v 3(p. T) in ALICE 22

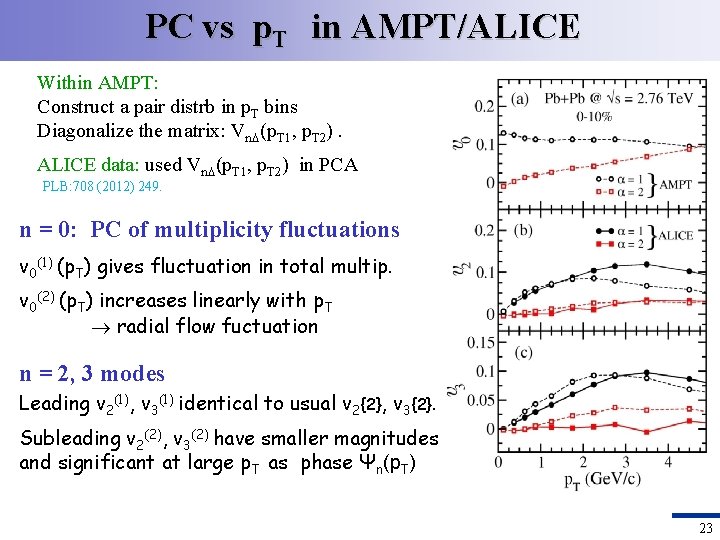
PC vs p. T in AMPT/ALICE Within AMPT: Construct a pair distrb in p. T bins Diagonalize the matrix: Vn (p. T 1, p. T 2). ALICE data: used Vn (p. T 1, p. T 2) in PCA PLB: 708 (2012) 249. n = 0: PC of multiplicity fluctuations v 0(1) (p. T) gives fluctuation in total multip. v 0(2) (p. T) increases linearly with p. T radial flow fuctuation n = 2, 3 modes Leading v 2(1), v 3(1) identical to usual v 2{2}, v 3{2}. Subleading v 2(2), v 3(2) have smaller magnitudes and significant at large p. T as phase Ψn(p. T) 23

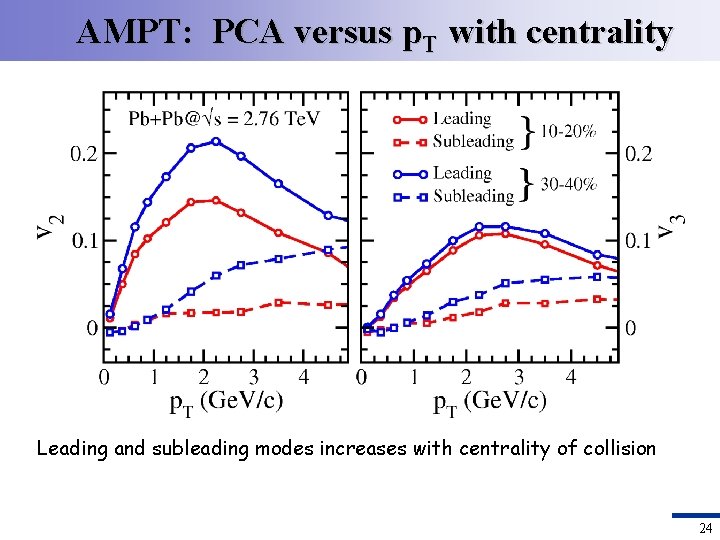
AMPT: PCA versus p. T with centrality Leading and subleading modes increases with centrality of collision 24

Ideal and Dissipative Hydrodynamics Israel, Stewart, Ann. Phys. 118 (1979) 341. Muronga, PRC 69 (2004) 034903. Romatschke, Int. J. Mod. Phys. E 19 (2010) 1. Huovinen, Petreczky, NPA 837 (2010) 26 s 95 p-PCE Eo. S matching lattice data to hadron reson gas at TPCE 165 Me. V Hadron spectra at freeze-out temp. Tdec 120 Me. V obtained by Cooper-Frye formula 25

Non-equilibrium distribution function Grad, Comm. Pure App. Math 2 (1949) 2 Chapman-Enskog like derivation Bhalerao, Jaiswal, SP, Sreekanth, PRC 89 (2014) 055903 26

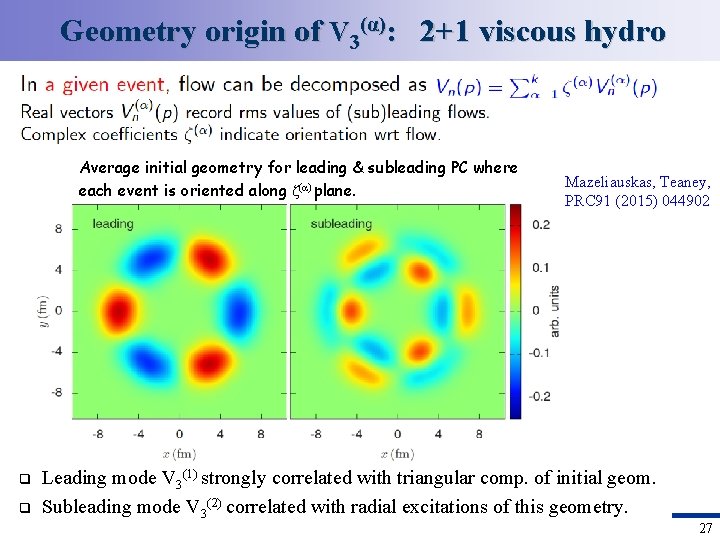
Geometry origin of V 3(α): 2+1 viscous hydro Average initial geometry for leading & subleading PC where each event is oriented along ζ(α) plane. q q Mazeliauskas, Teaney, PRC 91 (2015) 044902 Leading mode V 3(1) strongly correlated with triangular comp. of initial geom. Subleading mode V 3(2) correlated with radial excitations of this geometry. 27

Viscosity dependence of PC for v 3 q q Leading mode v 3(1) strongly suppressed with shear viscosity. Subleading flow v 3(2) depends weakly on viscosity and centrality. 28

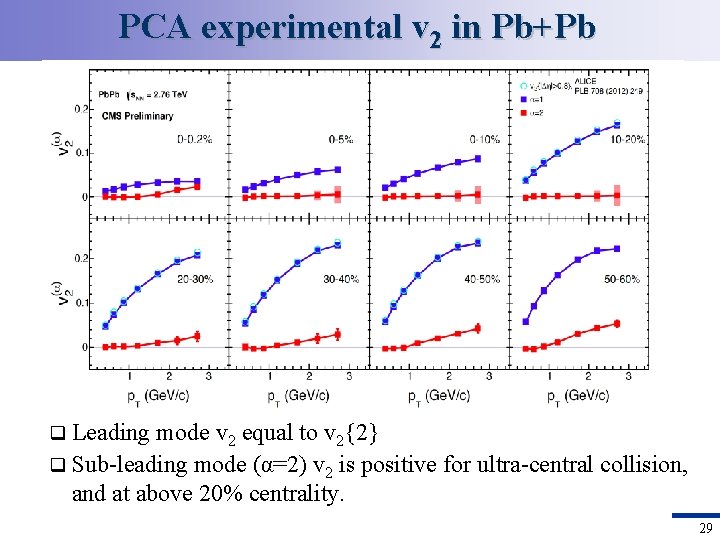
PCA experimental v 2 in Pb+Pb Leading mode v 2 equal to v 2{2} q Sub-leading mode (α=2) v 2 is positive for ultra-central collision, and at above 20% centrality. q 29

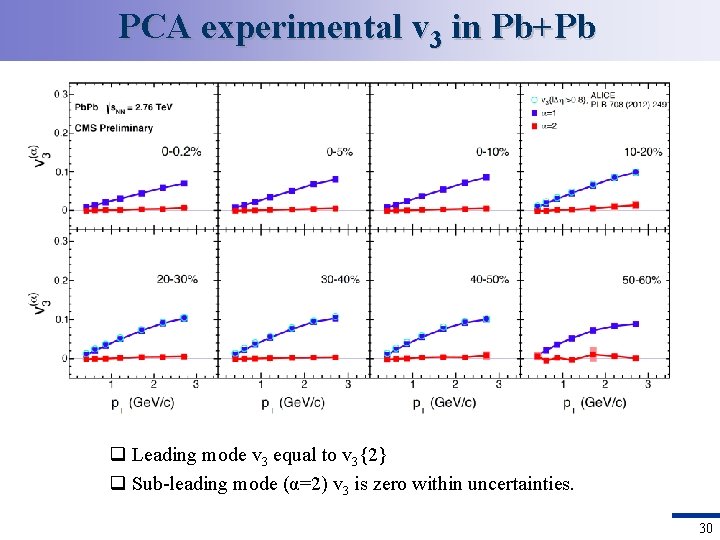
PCA experimental v 3 in Pb+Pb q Leading mode v 3 equal to v 3{2} q Sub-leading mode (α=2) v 3 is zero within uncertainties. 30

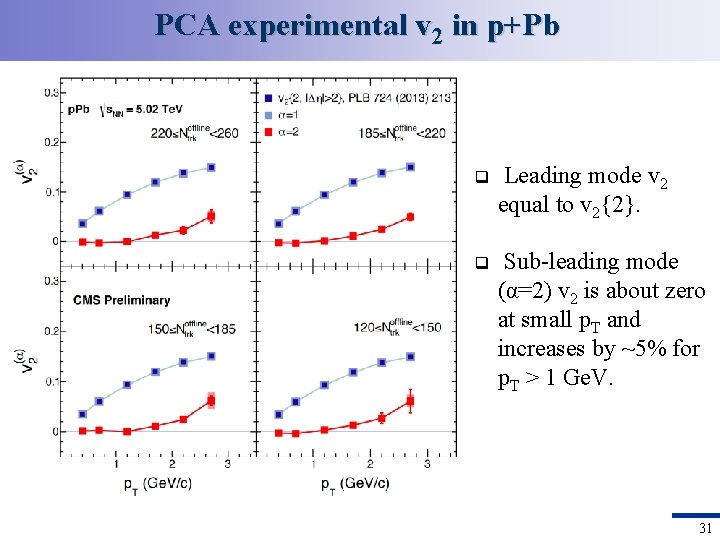
PCA experimental v 2 in p+Pb q Leading mode v 2 equal to v 2{2}. q Sub-leading mode (α=2) v 2 is about zero at small p. T and increases by ~5% for p. T > 1 Ge. V. 31

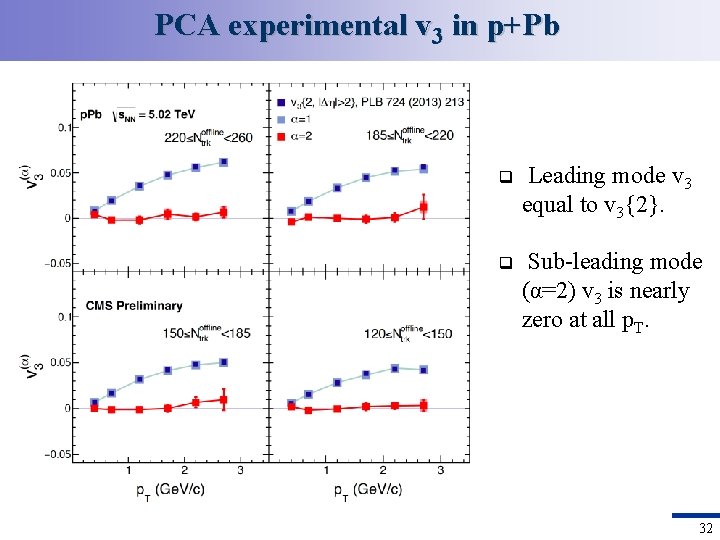
PCA experimental v 3 in p+Pb q Leading mode v 3 equal to v 3{2}. q Sub-leading mode (α=2) v 3 is nearly zero at all p. T. 32

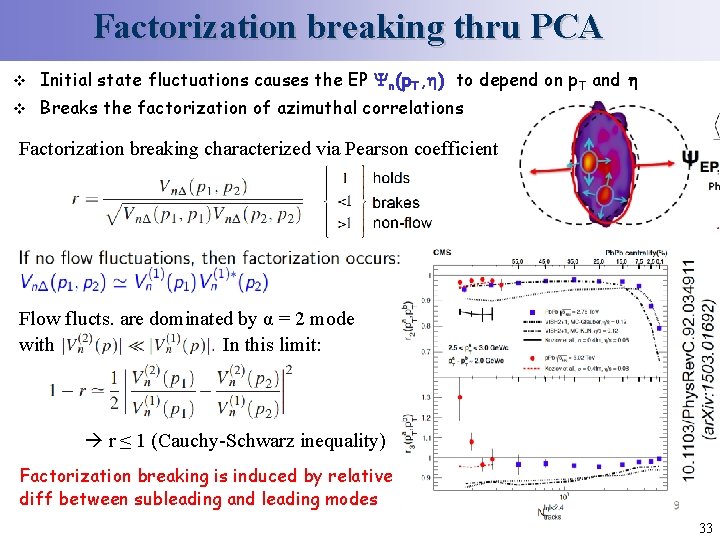
Factorization breaking thru PCA v Initial state fluctuations causes the EP n(p. T, ) to depend on p. T and v Breaks the factorization of azimuthal correlations Factorization breaking characterized via Pearson coefficient Flow flucts. are dominated by α = 2 mode with ` In this limit: r ≤ 1 (Cauchy-Schwarz inequality) Factorization breaking is induced by relative diff between subleading and leading modes 33

Summary & Conclusions PCA can provide further constraints on the properties of QGP ! 34