Prims Minimum Spanning Tree Algorithm CSCI 385 Data

  • Slides: 18
Download presentation
Prim’s Minimum Spanning Tree Algorithm CSCI 385 Data Structures & Analysis of Algorithms Lecture

Prim’s Minimum Spanning Tree Algorithm CSCI 385 Data Structures & Analysis of Algorithms Lecture note Sajedul Talukder

Prim’s Algorithm Maintain two disjoint sets of vertices. One containing vertices that are in

Prim’s Algorithm Maintain two disjoint sets of vertices. One containing vertices that are in the growing spanning tree and other that are not in the growing spanning tree. Three Steps: 1. Start with an arbitrary node and add it to the MST set. 2. Select the next shortest edge from the neighbors of MST set that does not create a cycle 3. Stop when you have added all the vertices to the MST set

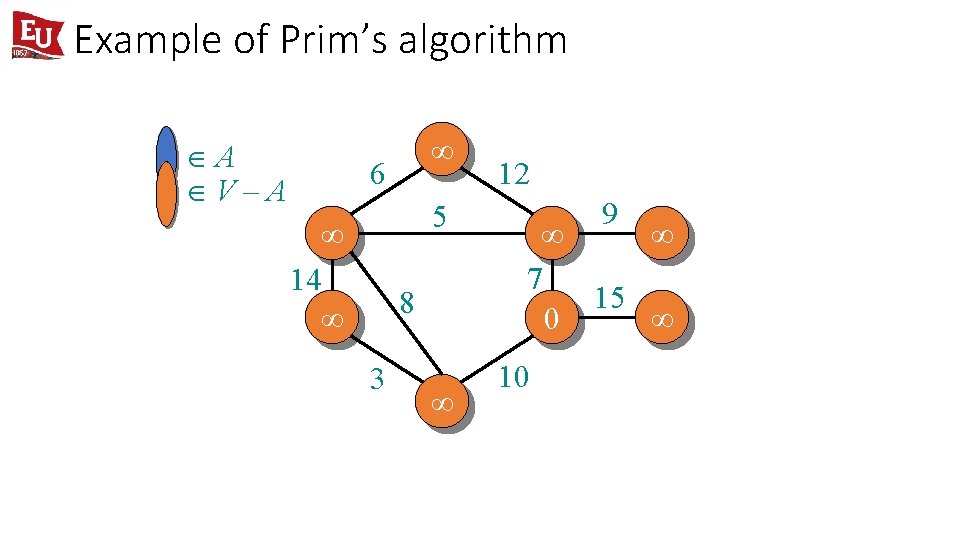
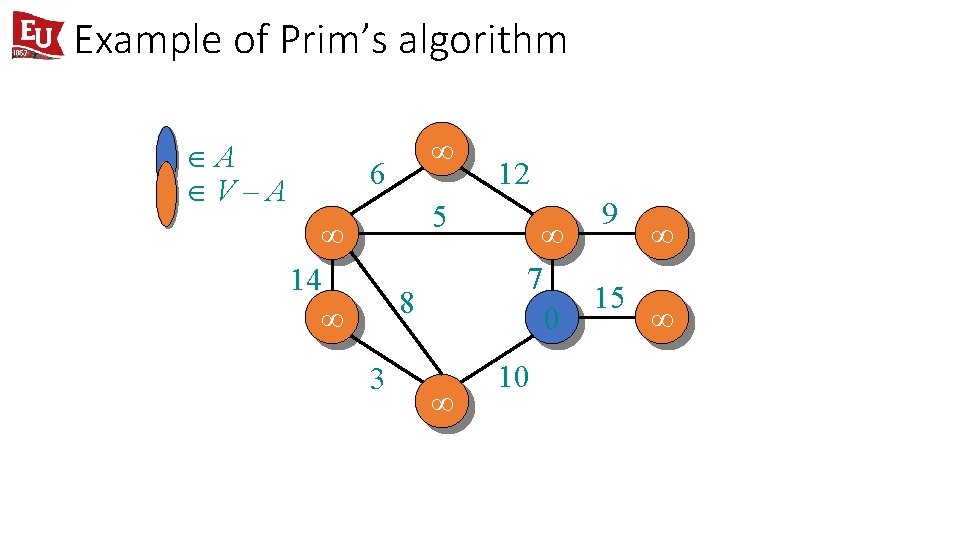
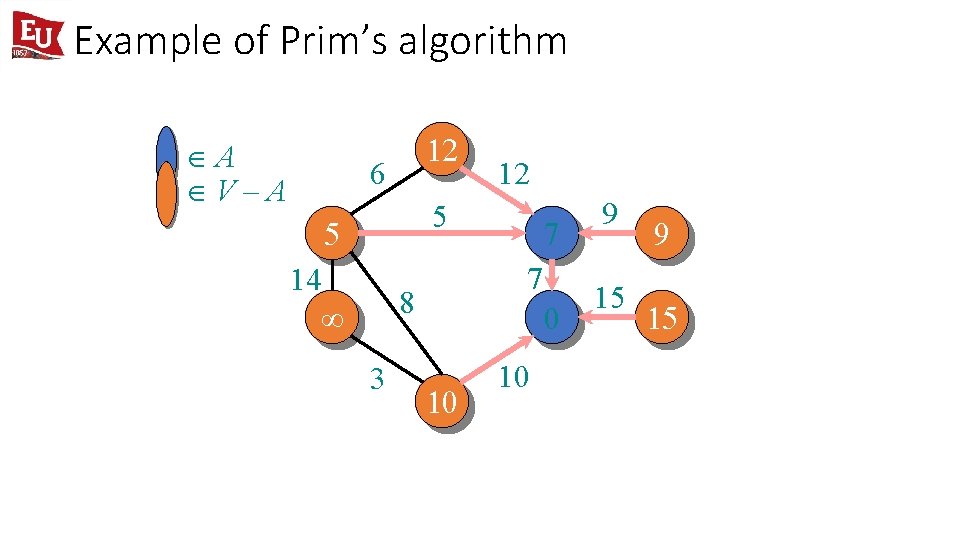
Example of Prim’s algorithm ÎA ÎV–A ¥ 6 5 ¥ 14 ¥ 8 3

Example of Prim’s algorithm ÎA ÎV–A ¥ 6 5 ¥ 14 ¥ 8 3 ¥ 12 9 ¥ ¥ 7 15 0 ¥ 10

Example of Prim’s algorithm ÎA ÎV–A ¥ 6 5 ¥ 14 ¥ 8 3

Example of Prim’s algorithm ÎA ÎV–A ¥ 6 5 ¥ 14 ¥ 8 3 ¥ 12 9 ¥ ¥ 7 15 0 ¥ 10

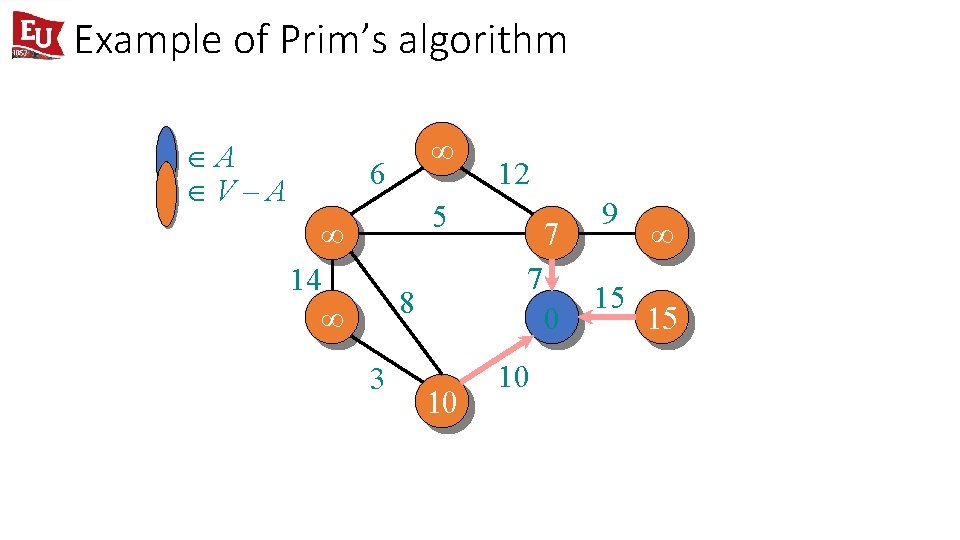
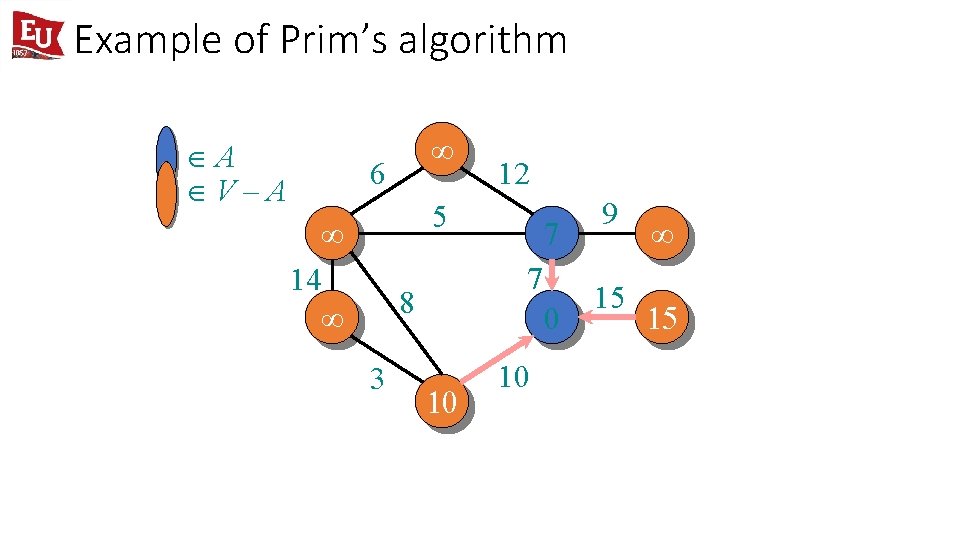
Example of Prim’s algorithm ÎA ÎV–A ¥ 6 12 5 ¥ 14 ¥ 7

Example of Prim’s algorithm ÎA ÎV–A ¥ 6 12 5 ¥ 14 ¥ 7 8 3 7 0 10 10 9 15 ¥ 15

Example of Prim’s algorithm ÎA ÎV–A ¥ 6 12 5 ¥ 14 ¥ 7

Example of Prim’s algorithm ÎA ÎV–A ¥ 6 12 5 ¥ 14 ¥ 7 8 3 7 0 10 10 9 15 ¥ 15

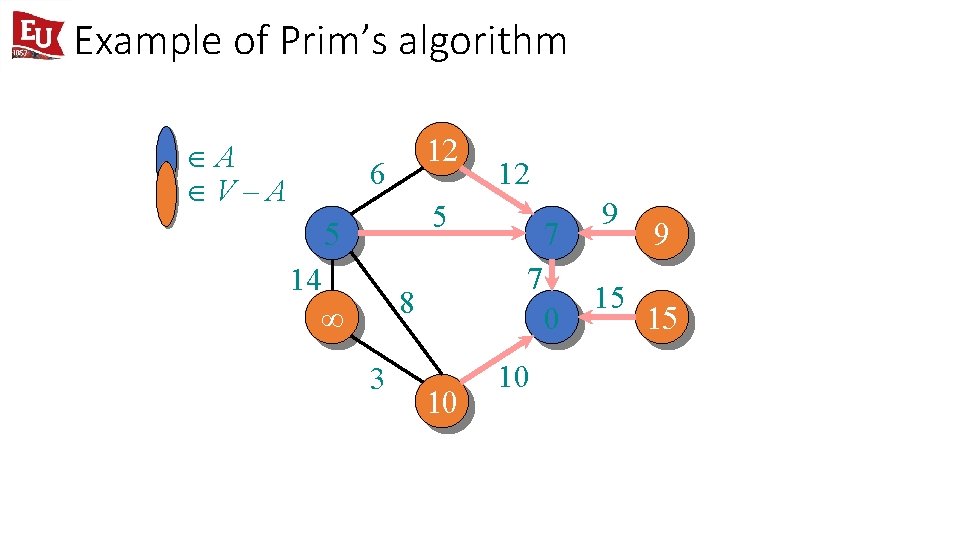
Example of Prim’s algorithm ÎA ÎV–A 12 6 12 5 5 14 ¥ 7

Example of Prim’s algorithm ÎA ÎV–A 12 6 12 5 5 14 ¥ 7 8 3 7 0 10 10 9 15

Example of Prim’s algorithm ÎA ÎV–A 12 6 12 5 5 14 ¥ 7

Example of Prim’s algorithm ÎA ÎV–A 12 6 12 5 5 14 ¥ 7 8 3 7 0 10 10 9 15

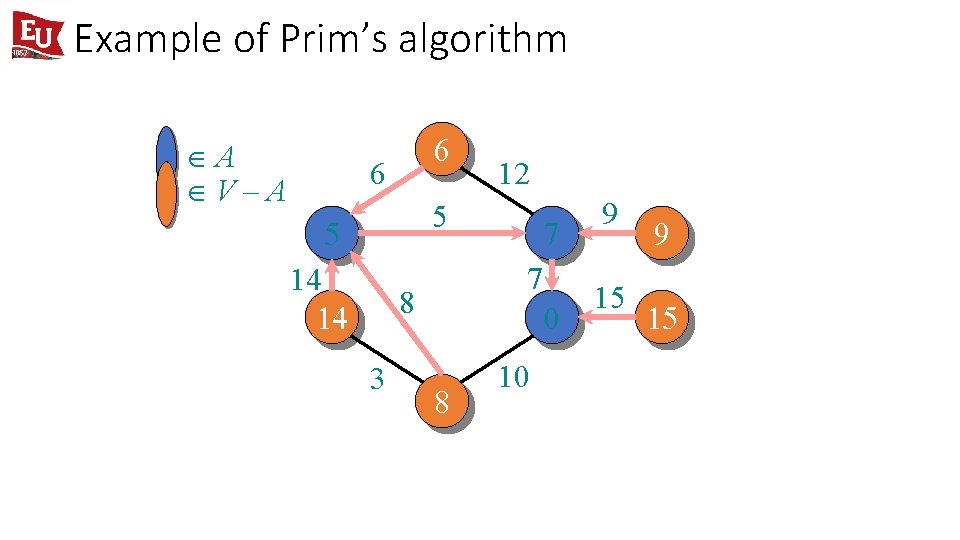
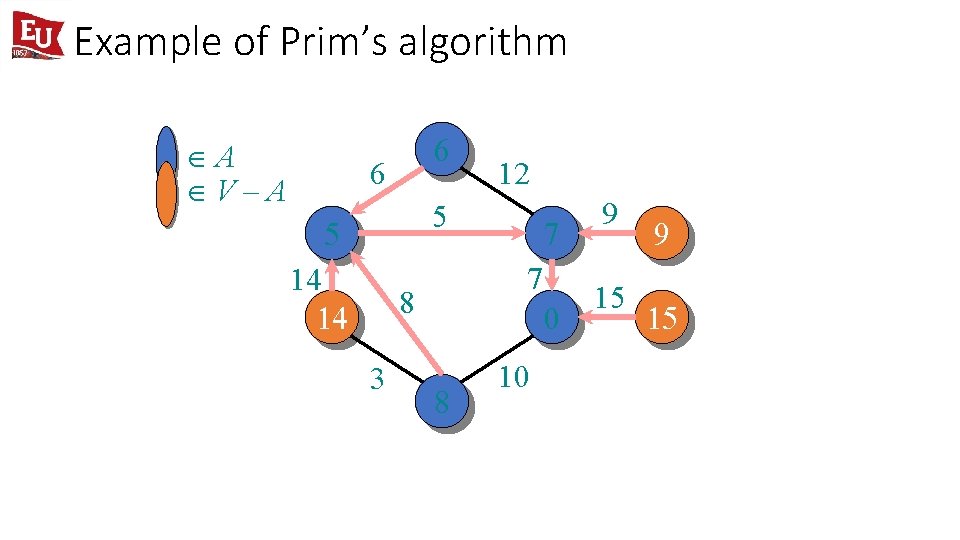
Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 14 7

Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 14 7 8 3 7 0 8 10 9 15

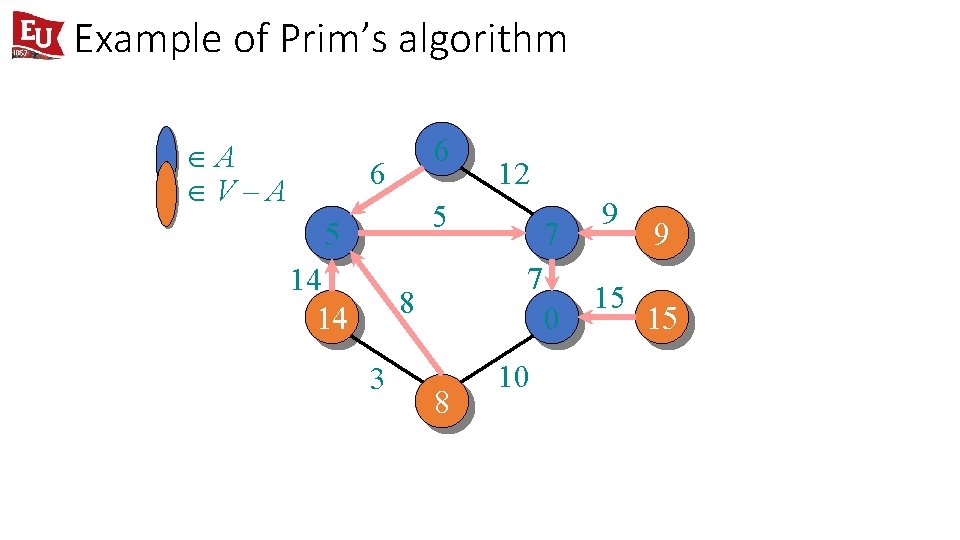
Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 14 7

Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 14 7 8 3 7 0 8 10 9 15

Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 14 7

Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 14 7 8 3 7 0 8 10 9 15

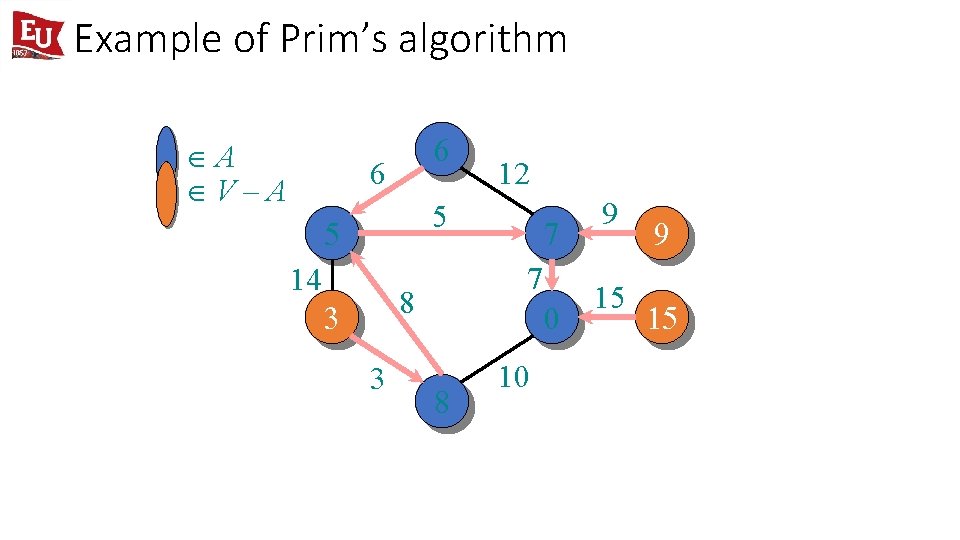
Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 7 8

Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 7 8 3 3 7 0 8 10 9 15

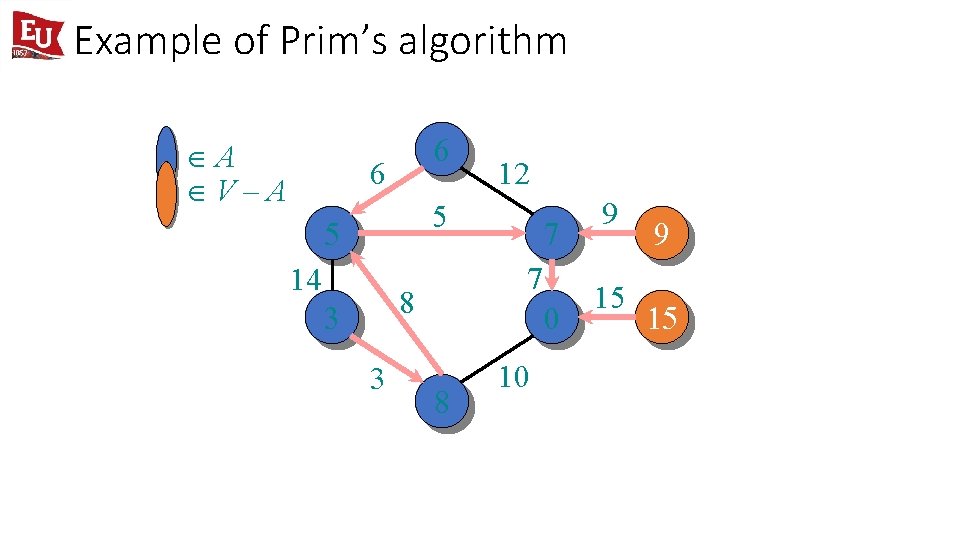
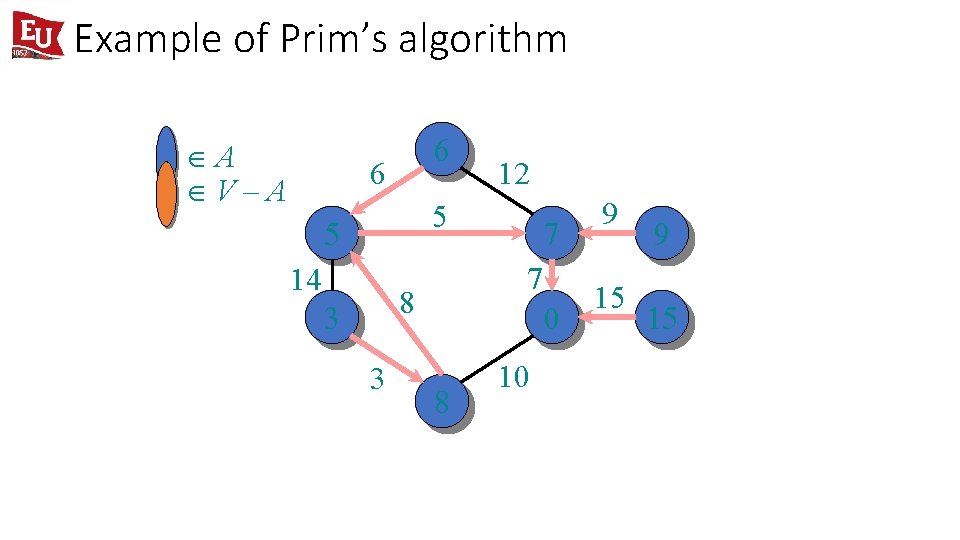
Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 7 8

Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 7 8 3 3 7 0 8 10 9 15

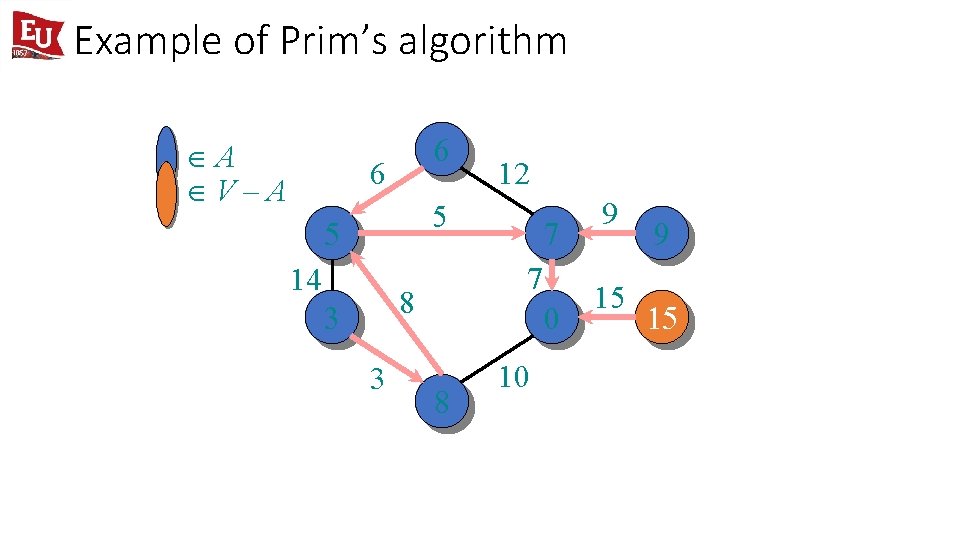
Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 7 8

Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 7 8 3 3 7 0 8 10 9 15

Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 7 8

Example of Prim’s algorithm ÎA ÎV–A 6 6 12 5 5 14 7 8 3 3 7 0 8 10 9 15

Example of Prim’s algorithm ÎA ÎV–A 6 6 5 5 7 8 3 3

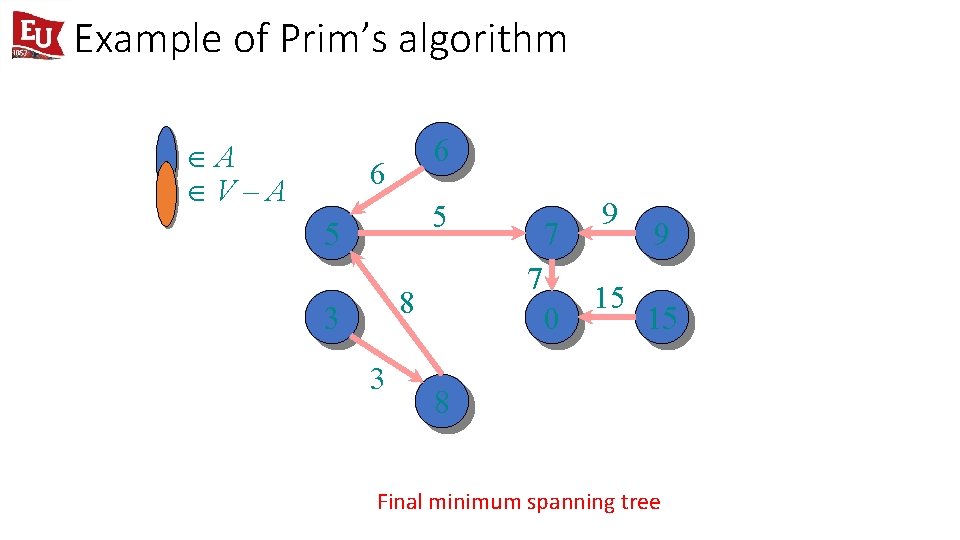
Example of Prim’s algorithm ÎA ÎV–A 6 6 5 5 7 8 3 3 7 0 9 15 8 Final minimum spanning tree

Prim’s Algorithm Pseudocode IDEA: Maintain V – A as a priority queue Q. Key

Prim’s Algorithm Pseudocode IDEA: Maintain V – A as a priority queue Q. Key each vertex in Q with the weight of the leastweight edge connecting it to a vertex in A. Q V key[v] ¥ for all v Î V key[s] 0 for some arbitrary s Î V while Q ¹ do u EXTRACT-MIN(Q) for each v Î Adj[u] do if v Î Q and w(u, v) < key[v] then key[v] w(u, v) ⊳ DECREASE-KEY ⊳ Add u to MST set At the end, {(v, p[v])} forms the MST. p[v] u

Prim’s Algorithm Complexity IDEA: Implement the priority queue Q with min-heap. Use adjacency list

Prim’s Algorithm Complexity IDEA: Implement the priority queue Q with min-heap. Use adjacency list to store the neighbors. Q V key[v] ¥ for all v Î V O(V) key[s] 0 for some arbitrary s Î V O(1) while Q ¹ O(V) do u EXTRACT-MIN(Q) O(log V) for each v Î Adj[u] O(E) do if v Î Q and w(u, v) < key[v] then key[v] w(u, v) p[v] u ⊳ DECREASE-KEY ⊳ Add u to MST set Total time complexity: O(V) + O(V)·TEXTRACT-MIN + O(E)·TDECREASE-KEY = O(V) + O(V log V) + O(E log V) = O(E log V) O(log V)