Prime Numbers and Prime Factorization Factors Factors are

Prime Numbers and Prime Factorization

Factors • Factors are the numbers you multiply together to get a product. • For example, the product 24 has several factors. • 24 = 1 x 24 • 24 = 2 x 12 • 24 = 3 x 8 • 24 = 4 x 6 • SO, the factors are 1, 2, 3, 4, 6, 8, 12, 24

Finding Factors • Start with 1 times the number. • Try 2, 3, 4, etc. • When you repeat your factors, cross out the repeat - you’re done at this point. • If you get doubles (such as 4 x 4), then you’re done. Repeats or doubles let you know you’re done.
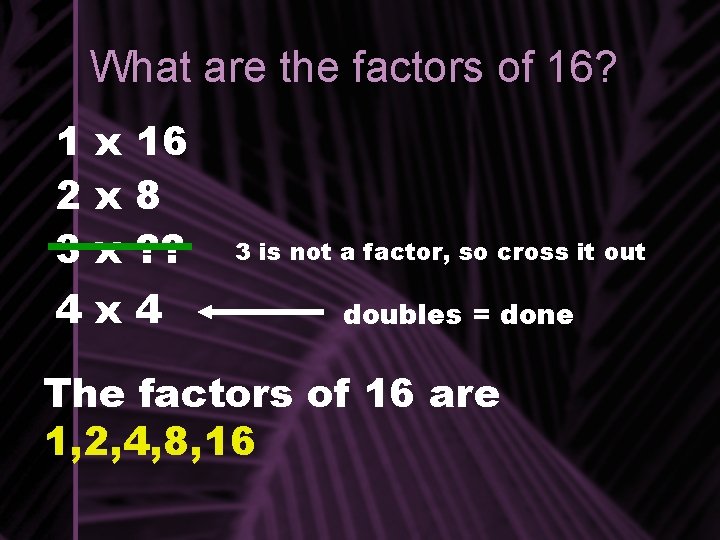
What are the factors of 16? 1 x 16 2 x 8 3 x ? ? 4 x 4 3 is not a factor, so cross it out doubles = done The factors of 16 are 1, 2, 4, 8, 16

What are the factors of 18? 1 2 3 4 5 6 x x x 18 9 6 ? ? 3 The factors are 1, 2, 3, 6, 9, 18 Repeat! Cross it out! We’re done!

What are the factors of 7? 1 x 7 2 x ? ? 3 x ? ? 4 5 6 7 x x ? ? ? 1 The only factors of 7 are 1, 7 This works, but it is a repeat. We are done.

Prime and Composite Numbers Prime numbers are numbers that only have two factors: one, and the number itself. EXAMPLES: 3, 5, 7, 11, 31 Composite numbers have more than two factors. EXAMPLES: 6, 15, 18, 30, 100

A Product of Primes • Every composite number can be expressed as a product of prime numbers. • This is called prime factorization.

Example • 15 is a composite number. • It can be written as a product of primes: 3 x 5

To find the prime factorization: 1. Divide the number by the first prime number possible. 2. Circle the prime number, and continue with the other factor. 3. Divide the new factor by a prime number. 4. Continue this process until the only numbers you have left are prime numbers.

Remember the Prime Number List: • 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97…
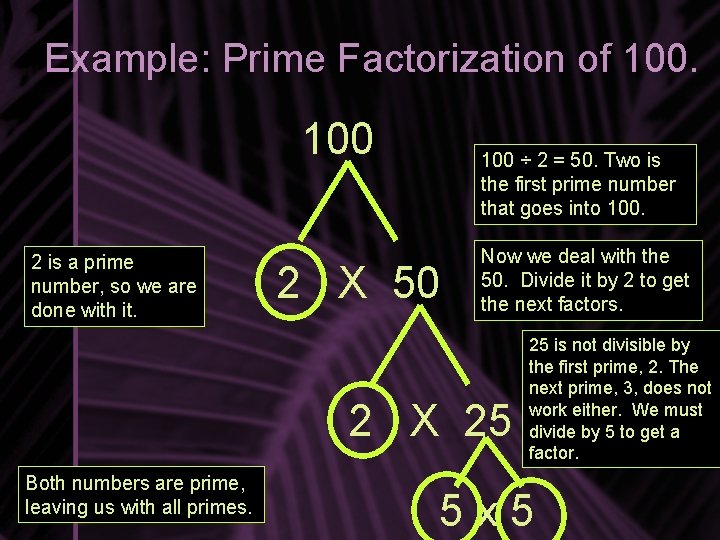
Example: Prime Factorization of 100 2 is a prime number, so we are done with it. 100 ÷ 2 = 50. Two is the first prime number that goes into 100. 2 X 50 Now we deal with the 50. Divide it by 2 to get the next factors. 2 X 25 Both numbers are prime, leaving us with all primes. 25 is not divisible by the first prime, 2. The next prime, 3, does not work either. We must divide by 5 to get a factor. 5 x 5

What’s the Answer? • Now, we just list our factors with multiplication signs between them. Use the circled prime numbers. • 2 x 2 x 5 x 5

Exponent Form • We have just listed our prime factorization for 100 as being 2 x 5 x 5. This is repeated multiplication. Repeated multiplication can be expressed with exponents. 2 • 2 x 2 can be expressed in exponent form: 2 • 5 x 5 can be expressed as 52 • Put it together, and 2 x 5 x 5 is more simply put as 2 2 x 52

Another Example 420 2 x 210 2 x 105 2 x 2 x 3 x 5 x 7 3 x 35 or 5 x 7 2 2 x 3 x 5 x 7

Try this on your own: 54 Answer: 2 x 3 x 3 x 3 or 2 x 3 3

Try this on your own:

Try this on your own:

Try this on your own:

Try this on your own:

Homework Time!
- Slides: 21