PrimalDual Algorithms for Connected Facility Location Chaitanya Swamy

Primal-Dual Algorithms for Connected Facility Location Chaitanya Swamy Amit Kumar Cornell University ALADDIN Workshop, 10/2002

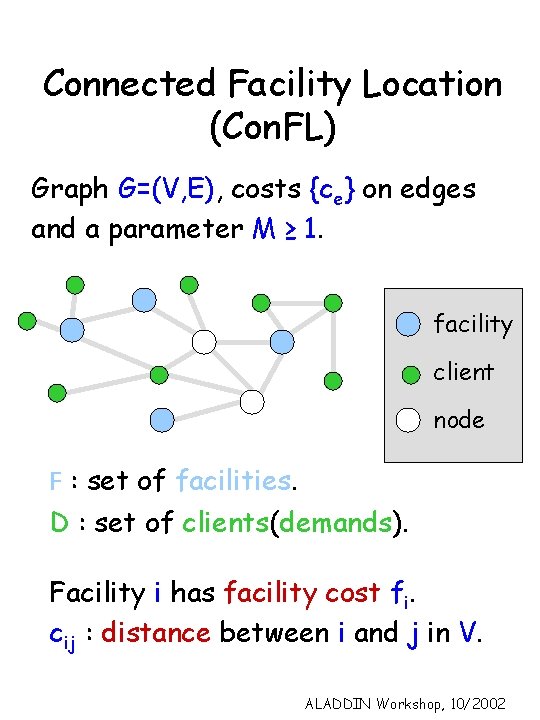
Connected Facility Location (Con. FL) Graph G=(V, E), costs {ce} on edges and a parameter M ≥ 1. facility client node F : set of facilities. D : set of clients(demands). Facility i has facility cost fi. cij : distance between i and j in V. ALADDIN Workshop, 10/2002

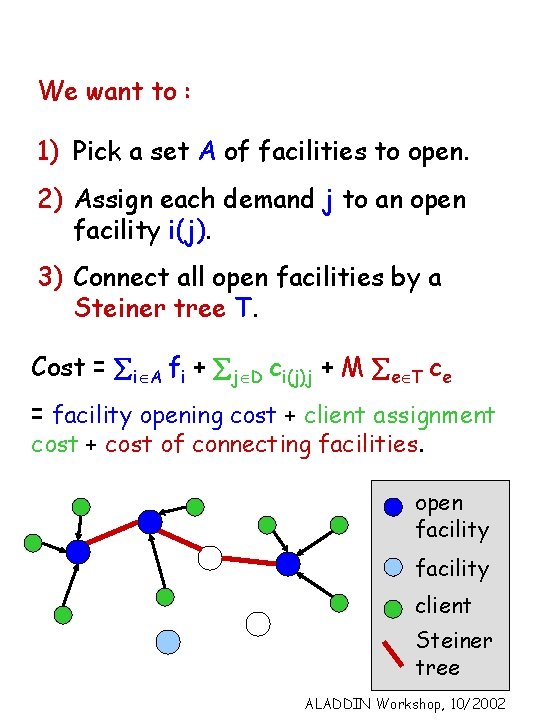
We want to : 1) Pick a set A of facilities to open. 2) Assign each demand j to an open facility i(j). 3) Connect all open facilities by a Steiner tree T. Cost = iÎA fi + jÎD ci(j)j + M eÎT ce = facility opening cost + client assignment cost + cost of connecting facilities. open facility client Steiner tree ALADDIN Workshop, 10/2002

Previous Work • Ravi & Selman : Look at related problem - connect facilities by a tour. Round optimal solution of an exponential size LP. • Karger & Minkoff : Combinatorial algorithm with ‘large’ constant approx. ratio. • Gupta, Kleinberg, Kumar, Rastogi & Yener : Also use LP rounding. Get a 9. 001 -approx. if F =V, fi = 0 for all i, a 10. 66 -approx. in the general case. • Guha, Meyerson & Munagala; Talwar : Gave a constant approx. for the single -sink buy-at-bulk problem. ALADDIN Workshop, 10/2002

Our Results • Give primal-dual algorithms with approx. ratios of 5 (F =V, fi = 0) and 9 (general case). • Use this to solve the Connected k-Median problem, and an edge capacitated version of Con. FL. ALADDIN Workshop, 10/2002

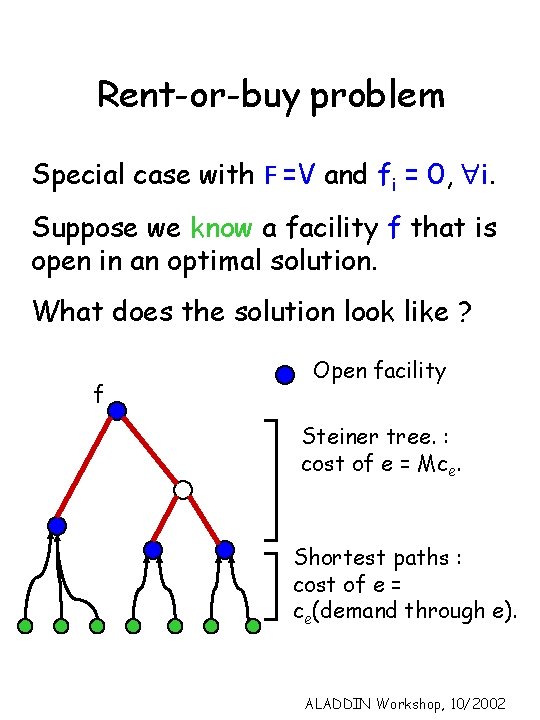
Rent-or-buy problem Special case with F =V and fi = 0, i. Suppose we know a facility f that is open in an optimal solution. What does the solution look like ? f Open facility Steiner tree. : cost of e = Mce. Shortest paths : cost of e = ce(demand through e). ALADDIN Workshop, 10/2002

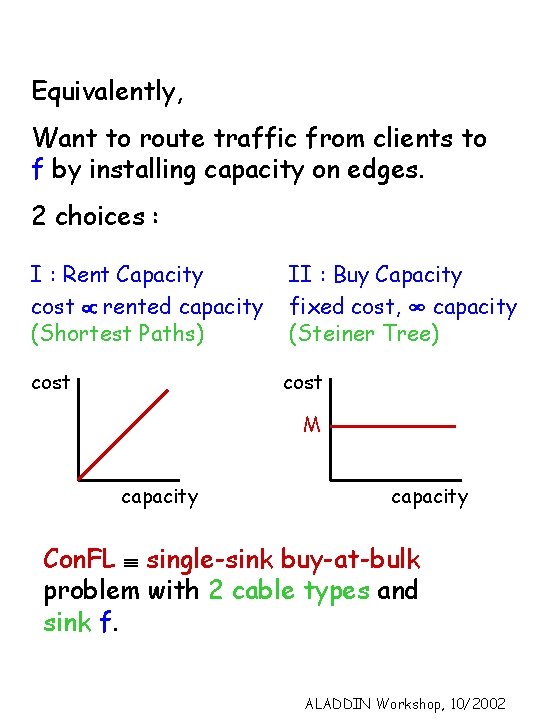
Equivalently, Want to route traffic from clients to f by installing capacity on edges. 2 choices : I : Rent Capacity cost µ rented capacity (Shortest Paths) II : Buy Capacity fixed cost, ∞ capacity (Steiner Tree) cost M capacity Con. FL º single-sink buy-at-bulk problem with 2 cable types and sink f. ALADDIN Workshop, 10/2002

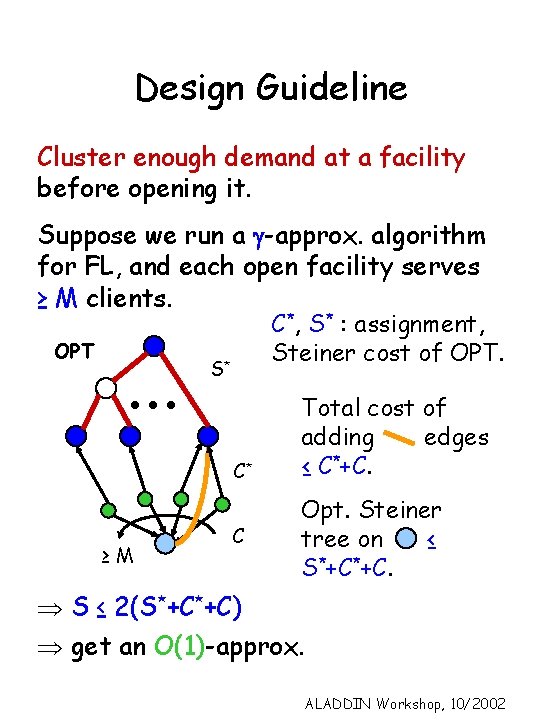
Design Guideline Cluster enough demand at a facility before opening it. Suppose we run a g-approx. algorithm for FL, and each open facility serves ≥ M clients. OPT C*, S* : assignment, Steiner cost of OPT. S* C* ≥M C Total cost of adding edges ≤ C*+C. Opt. Steiner tree on ≤ S*+C*+C. Þ S ≤ 2(S*+C*+C) Þ get an O(1)-approx. ALADDIN Workshop, 10/2002

An Integer Program xij = 1 if demand j is assigned to i. ze = 1 if edge e is included in the Steiner tree. Min. j, i cijxij + M e ceze (primal) s. t. i xij ≥ 1 f j iÎS xij ≤ eÎ (S) ze S Í V : fÏS, j xij, ze Î {0, 1} (1) S j Relax (1) to xij, ze ≥ 0 to get an LP. ALADDIN Workshop, 10/2002

What is the dual? vj º amount j is willing to ‘pay’ to route its demand to f. Let y. S = j y. S, j. {y. S } º moat packing around facilities. f vj ≤ cij + S: iÎS, fÏS y. S, j S: eÎ (S), fÏS y. S ≤ Mce cij Max. j vj j Any feasible dual solution is a lower bound on OPT – Weak Duality. ALADDIN Workshop, 10/2002

The Algorithm 1) Decide which facilities to open, cluster demands around open facilities. Construct a primal soln. and dual soln. (v, y) simultaneously. 2) Build a Steiner tree on open facilities. The following will hold after 1) : • (v, y) is a feasible dual solution. • j is assigned to i(j) s. t. ci(j)j ≤ 3 vj. • Each open facility i has ≥ M clients, {j}, assigned to it s. t. cij ≤ vj. ALADDIN Workshop, 10/2002

Analysis Suppose the 3 properties hold. Let A be the set of facilities opened, Di = {j assigned to i : cij ≤ vj } for iÎA. Then, |Di| ≥ M. Let D 1 = UiÎA Di. C ≤ jÎD 1 vj + jÏD 1 3 vj. can amortize the cost against demands in Di. Di ≥M i So, S ≤ 2(S*+ C* + jÎD 1 vj). ALADDIN Workshop, 10/2002

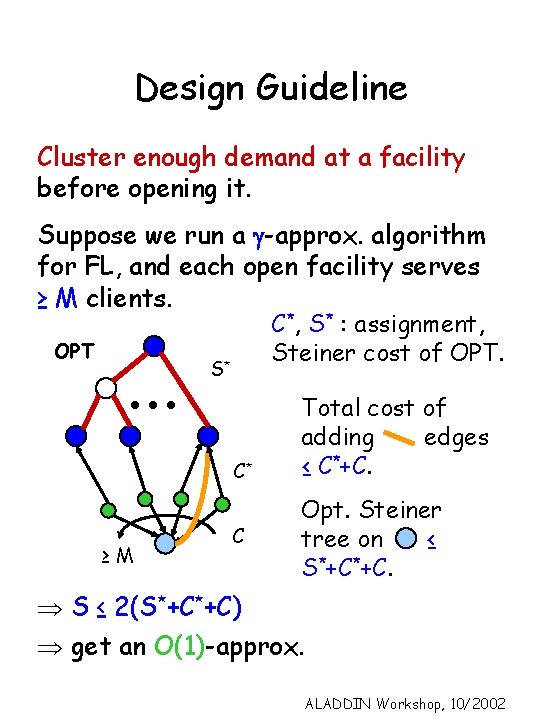
Design Guideline Cluster enough demand at a facility before opening it. Suppose we run a g-approx. algorithm for FL, and each open facility serves ≥ M clients. OPT C*, S* : assignment, Steiner cost of OPT. S* C* ≥M C Total cost of adding edges ≤ C*+C. Opt. Steiner tree on ≤ S*+C*+C. Þ S ≤ 2(S*+C*+C) Þ get an O(1)-approx. ALADDIN Workshop, 10/2002

Analysis Suppose the 3 properties hold. Let A be the set of facilities opened, Di = {j assigned to i : cij ≤ vj } for iÎA. Then, |Di| ≥ M. Let D 1 = UiÎA Di. C ≤ jÎD 1 vj + jÏD 1 3 vj. can amortize the cost against demands in Di. Di ≥M i So, S ≤ 2(S*+ C* + jÎD 1 vj). Total cost ≤ 2(S*+ C*) + 3 jÎD vj ≤ 5 OPT. ALADDIN Workshop, 10/2002

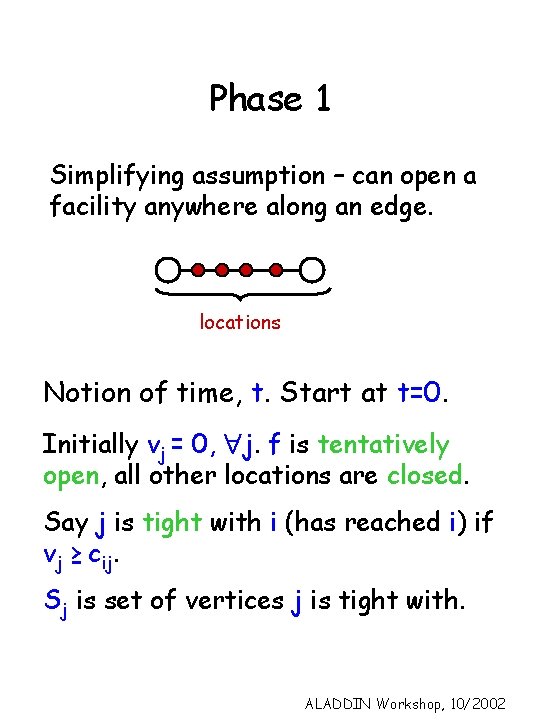
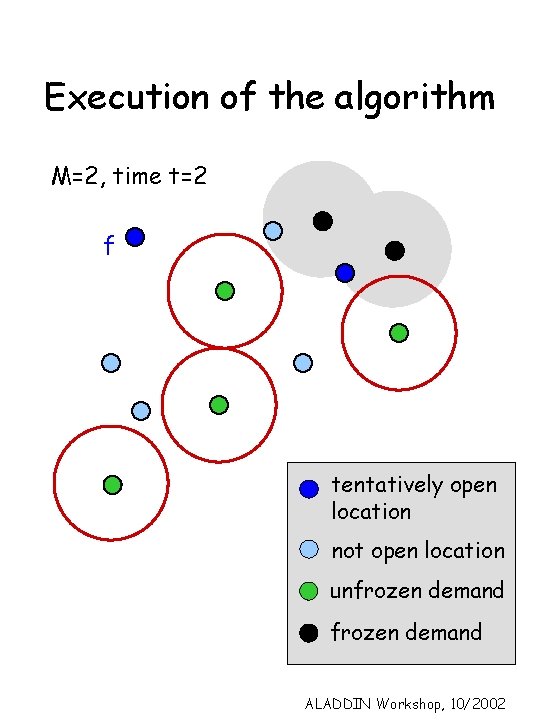
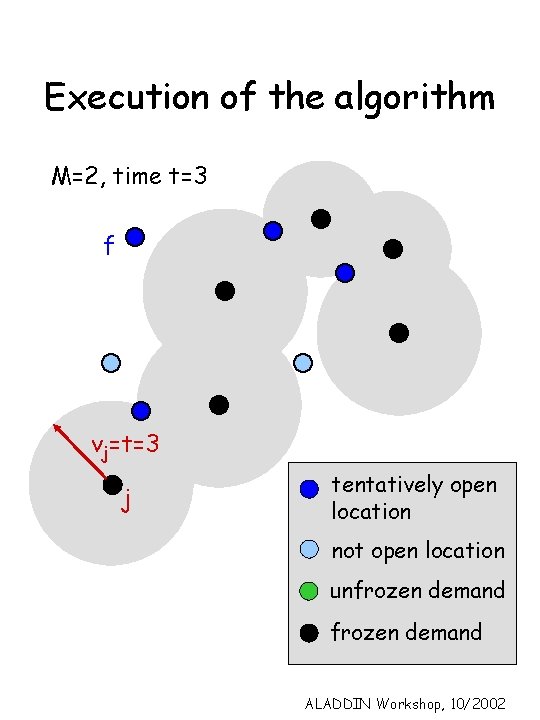
Phase 1 Simplifying assumption – can open a facility anywhere along an edge. locations Notion of time, t. Start at t=0. Initially vj = 0, j. f is tentatively open, all other locations are closed. Say j is tight with i (has reached i) if vj ≥ cij. Sj is set of vertices j is tight with. ALADDIN Workshop, 10/2002

Raise all vj at rate 1. Also raise y. Sj, j at same rate. Keep raising vjs until : 1) There is a closed location i with which M demands become tight : tentatively open i. Freeze all these M demands. 2) j reaches a tentatively open location : freeze j. Now only raise vj of unfrozen demands. Continue this process until all demands are frozen. ALADDIN Workshop, 10/2002

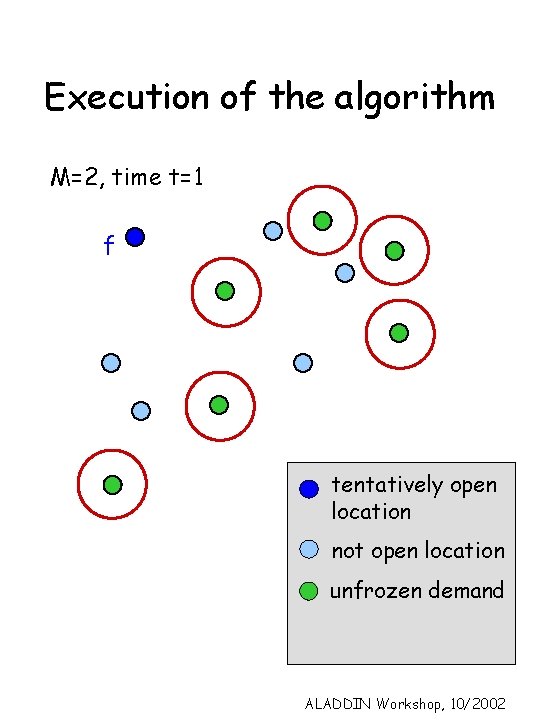
Execution of the algorithm t=1 M=2, time t=0 f tentatively open location not open location unfrozen demand ALADDIN Workshop, 10/2002

Execution of the algorithm M=2, time t=2 f tentatively open location not open location unfrozen demand ALADDIN Workshop, 10/2002

Execution of the algorithm M=2, time t=3 f vj=t=3 j tentatively open location not open location unfrozen demand ALADDIN Workshop, 10/2002

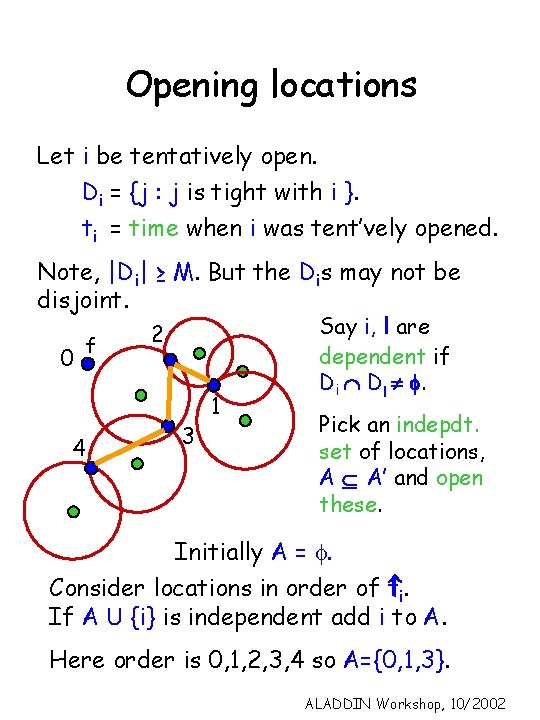
Opening locations Let i be tentatively open. Di = {j : j is tight with i }. ti = time when i was tent’vely opened. Note, |Di| ≥ M. But the Dis may not be disjoint. 0 f 4 2 3 1 Say i, l are dependent if Di Ç Dl ¹ f. Pick an indepdt. set of locations, A Í A’ and open these. Initially A = f. Consider locations in order of ti. If A U {i} is independent add i to A. Here order is 0, 1, 2, 3, 4 so A={0, 1, 3}. ALADDIN Workshop, 10/2002

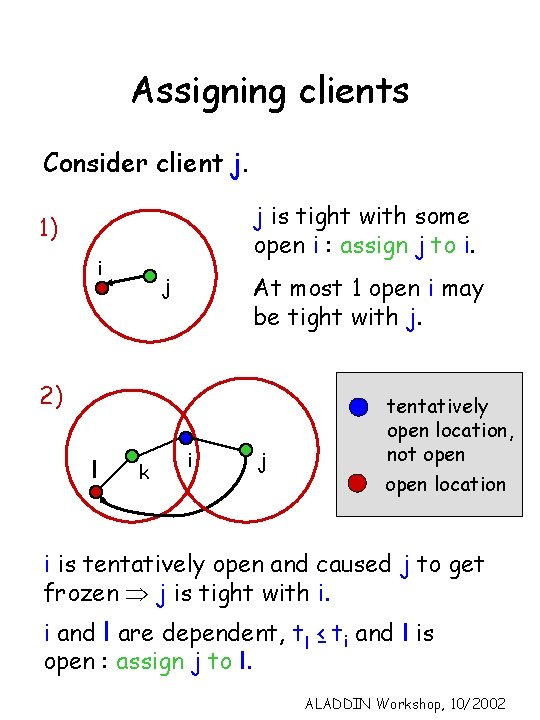
Assigning clients Consider client j. j is tight with some open i : assign j to i. 1) i At most 1 open i may be tight with j. j 2) l k i j tentatively open location, not open location i is tentatively open and caused j to get frozen Þ j is tight with i. i and l are dependent, tl ≤ ti and l is open : assign j to l. ALADDIN Workshop, 10/2002

i(j) = location that j is assigned to. 1) ci(j)j ≤ vj. 2) ci(j)j ≤ vj+ 2 vk. vj ≥ t i since j freezes at or after time ti. Also vk ≤ ti. So vk ≤ vj and ci(j)j ≤ 3 vj. For every open i, all clients in Di are assigned to i. |Di| ≥ M, so at least M demands {j} are assigned to i with cij ≤ vj. ALADDIN Workshop, 10/2002

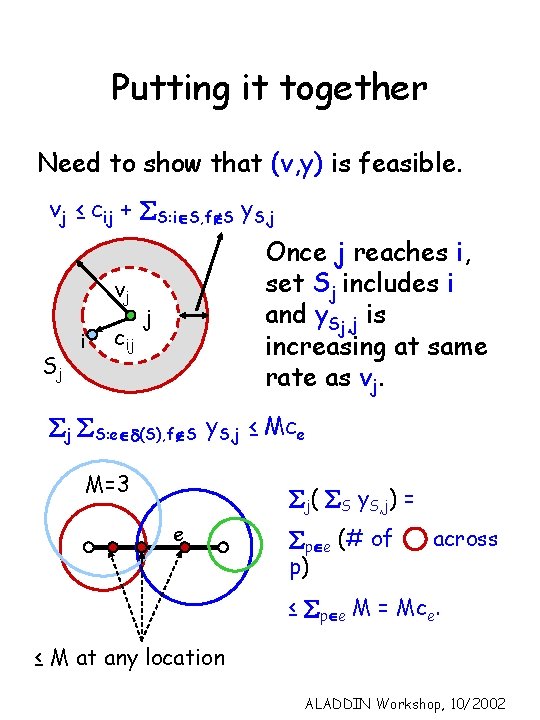
Putting it together Need to show that (v, y) is feasible. vj ≤ cij + S: iÎS, fÏS y. S, j vj Sj i cij Once j reaches i, set Sj includes i and y. Sj, j is increasing at same rate as vj. j j S: eÎ (S), fÏS y. S, j ≤ Mce M=3 j( S y. S, j) = e pÎe (# of p) across ≤ pÎe M = Mce. ≤ M at any location ALADDIN Workshop, 10/2002

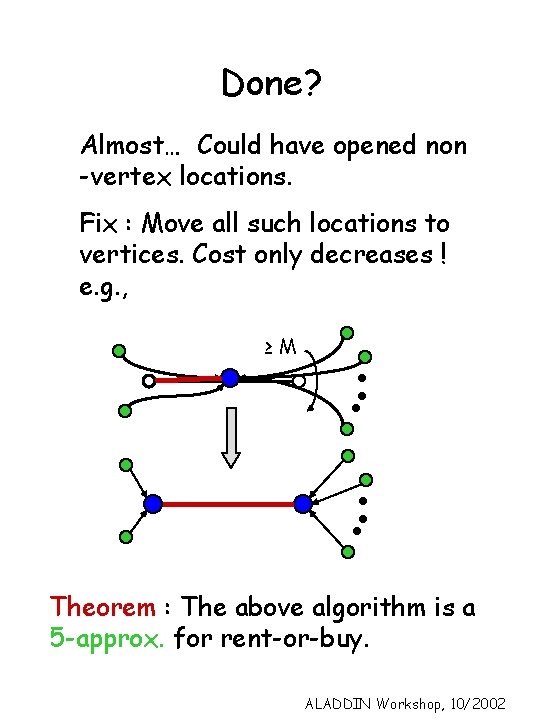
Done? Almost… Could have opened non -vertex locations. Fix : Move all such locations to vertices. Cost only decreases ! e. g. , ≥M Theorem : The above algorithm is a 5 -approx. for rent-or-buy. ALADDIN Workshop, 10/2002

The General Case • F Í V : Cannot open a facility everywhere. • Facilities have costs : Want to open cheap facilities. Modified Phase 1 1) Dual variables, vj, also pay for opening facilities. 2) Cluster ≥ M demands around terminal locations, open facilities ‘near’ terminal locations. Theorem : There is a 9 -approx. algorithm for the general case. ALADDIN Workshop, 10/2002

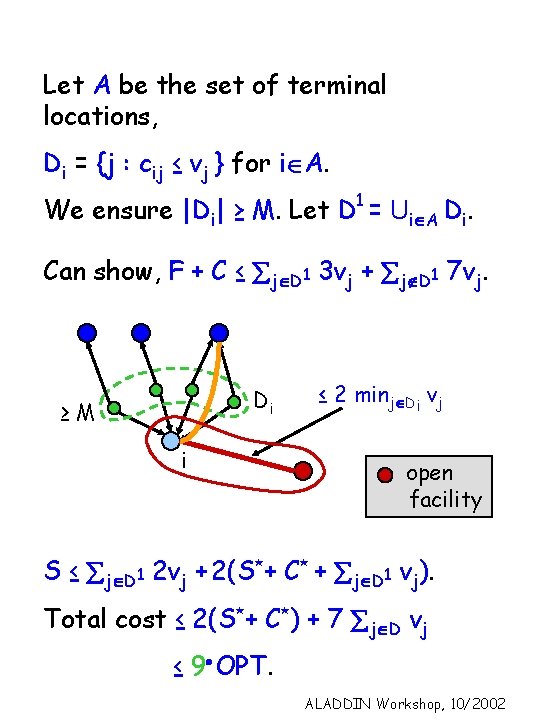
Let A be the set of terminal locations, Di = {j : cij ≤ vj } for iÎA. We ensure |Di| ≥ M. Let D 1 = UiÎA Di. Can show, F + C ≤ jÎD 1 3 vj + jÏD 1 7 vj. Di ≥M i ≤ 2 minjÎDi vj open facility S ≤ jÎD 1 2 vj + 2(S*+ C* + jÎD 1 vj). Total cost ≤ 2(S*+ C*) + 7 jÎD vj ≤ 9 OPT. ALADDIN Workshop, 10/2002

Open Questions 1) Better approximation : only know an integrality gap of 2 from Steiner tree. 2) Multicommodity buy-at-bulk. Multiple source-sink pairs, route flow from source to sink. Have different cable types. Kumar et al. give a const. approx. for multicommodity rent-or-buy. 3) Unrelated metrics : Min. i fiyi + j, i cijxij + e deze. Can reduce from group Steiner tree – get a O(log 2 n) LB. Matching UB? ALADDIN Workshop, 10/2002