Pricing and capital allocation for unitlinked life insurance

Pricing and capital allocation for unit-linked life insurance contracts with minimum death guarantee C. Frantz, X. Chenut and J. F. Walhin Secura Belgian Re

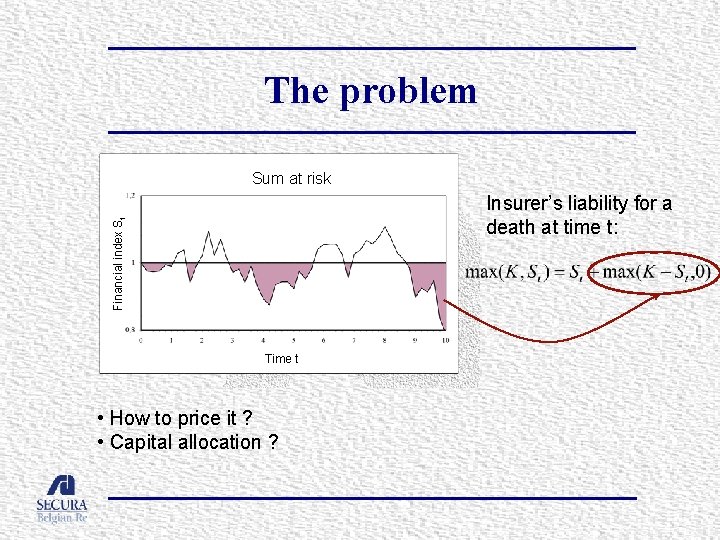
The problem Sum at risk Financial index St Insurer’s liability for a death at time t: Time t • How to price it ? • Capital allocation ?

Two approaches … § The financer: it is a contingent claim § Solution: hedging on the financial market Black-Scholes put pricing formula § The actuary: it is an insurance contract § Solution: equivalence principle Expected value of future losses

… and two risk managements § Financial approach : hedging on financial markets § Actuarial approach : reserving and raising capital

Agenda § § Actuarial vs financial pricing Monte Carlo simulations Cash flow model Open questions

First question: actuarial or financial pricing? § Hypotheses : – Complete and arbitrage-free financial market – Constant risk-free interest rate – Financial index follows a GBM: Simple expressions for the single pure premium in both approaches

Single pure premiums Actuarial pricing : Financial pricing : with

Monte Carlo simulations § Goal : distribution of the future costs § 3 processes to simulate : – Financial index – Death process – Hedging strategy (financial approach only)

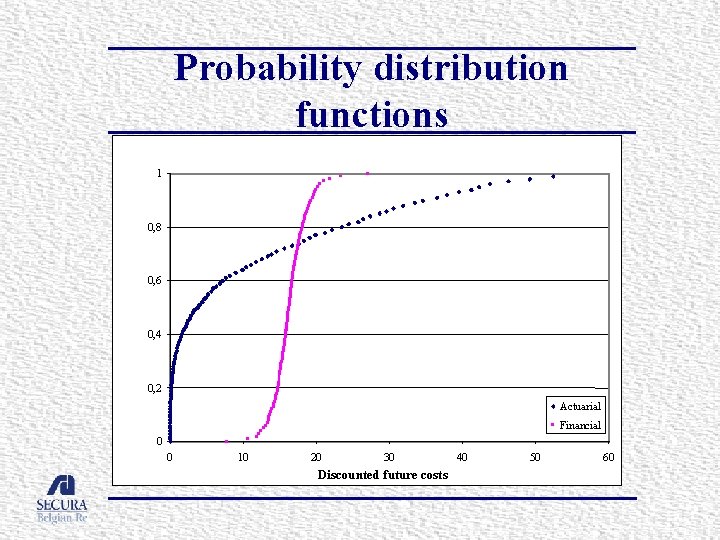
Probability distribution functions 1 0, 8 0, 6 0, 4 0, 2 Actuarial Financial 0 0 10 20 30 Discounted future costs 40 50 60

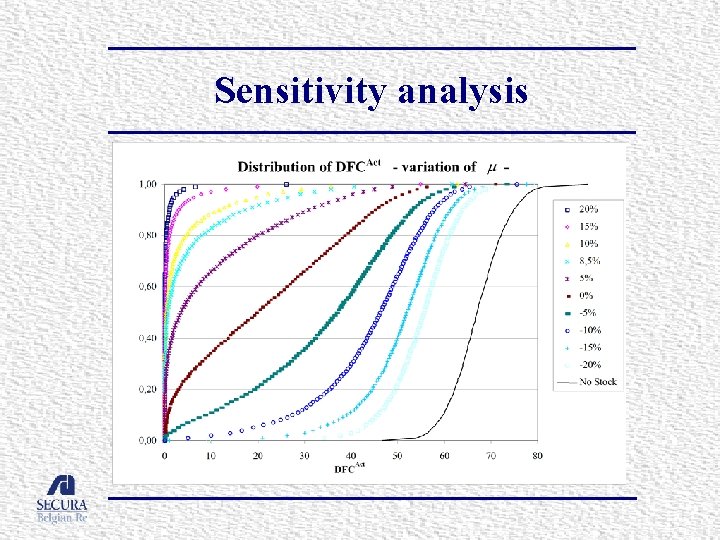
Sensitivity analysis

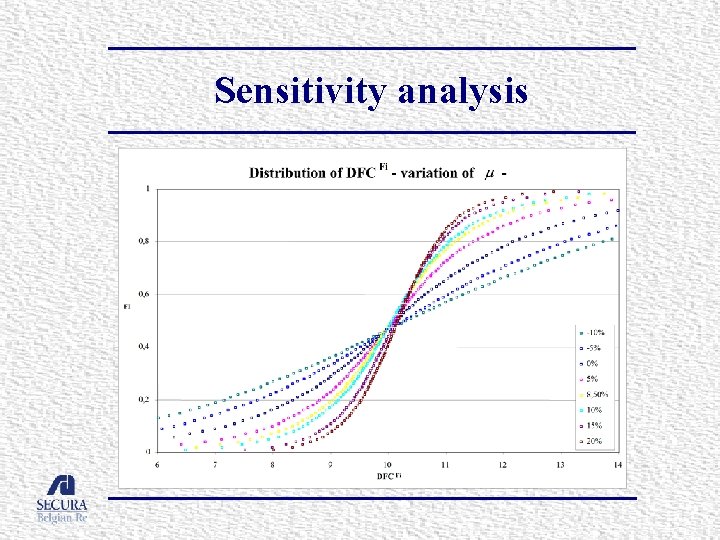
Sensitivity analysis

Conclusion § Financial approach is better § BUT only makes sense if the hedging strategy is applied ! § Difficult to put into practice (especially for the reinsurer) § Conclusion : actuarial approach has to be used

Second question : How to fix the price ? § Base : single pure premium § + Loading for « risk » § Answer : cash flow model

Cash flow model § Insurance contract = investment by the shareholders § Investment decision: cash flow model § Price P fixed according to the NPV criterion

Open questions § How much capital to allocate? § How to release it through time? § What is the cost of capital?

Risk measures and capital allocation § Coherent risk measures (Artzner et al. ) § Conditional tail expectation (CTE): where § Capital to be allocated at time t:

One-period vs multiperiodic risk measures § Problem: intermediate actions during development of risk § Addressed recently by Artzner et al. § Capital at time t : – to cover all the discounted future losses? – to pay the losses for x years and set up provisions at the end of the period? § We applied the one-period risk measure to the distribution of future losses at each time t

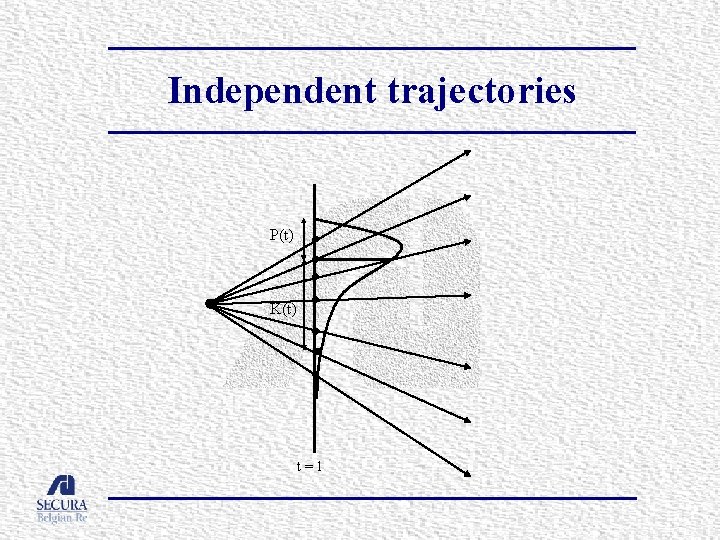
Simulation of provisions and capital § Two possibilities: – Independent trajectories

Independent trajectories P(t) K(t) t=1

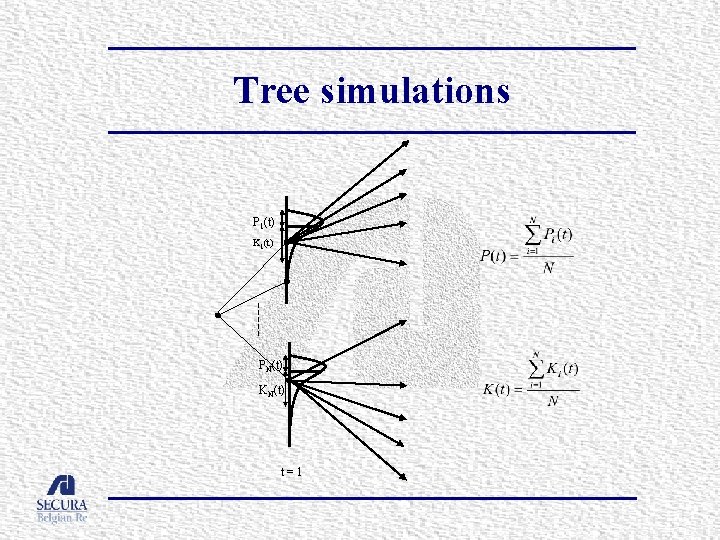
Simulation of provisions and capital § Two possibilities: – Independent trajectories – Tree simulations

Tree simulations P 1(t) K 1(t) PN(t) KN(t) t=1

Simulation of provisions and capital § Two possibilities: – Independent trajectories – Tree simulations

Cost of capital § CAPM : § What is the b for this contract? – Same b for the whole company? – Specific b for this line of business? § How to estimate it?

Conclusions § Actuarial approach § Pricing and capital allocation using simulations § Other questions: – Asset model: GBM, regime switching models, (G)ARCH, Jump diffusion, …? – Risk measure? Threshold a? – Capital allocation and release through time?