Price Discrimination and Monopoly Chapter 5 Price Discrimination







































- Slides: 59

Price Discrimination and Monopoly Chapter 5: Price Discrimination and Monopoly 1

Introduction • Prescription drugs are cheaper in Canada than the United States • Textbooks are generally cheaper in Britain than the United States • Examples of price discrimination – presumably profitable – should affect market efficiency: not necessarily adversely – is price discrimination necessarily bad – even if not seen as “fair”? Chapter 5: Price Discrimination and Monopoly 2

Feasibility of price discrimination • Two problems confront a firm wishing to price discriminate – identification: the firm is able to identify demands of different types of consumer or in separate markets • easier in some markets than others: e. g tax consultants, doctors – arbitrage: prevent consumers who are charged a low price from reselling to consumers who are charged a high price • prevent re-importation of prescription drugs to the United States • The firm then must choose the type of price discrimination – first-degree or personalized pricing – second-degree or menu pricing – third-degree or group pricing Chapter 5: Price Discrimination and Monopoly 3

Introduction to First-Degree Price Discrimination • Annual subscriptions generally cost less in total than one-off purchases • Buying in bulk usually offers a price discount – these are price discrimination reflecting quantity discounts – prices are nonlinear, with the unit price dependent upon the quantity bought – allows pricing nearer to willingness to pay – so should be more profitable than third-degree price discrimination • How to design such pricing schemes? – depends upon the information available to the seller about buyers – distinguish first-degree (personalized) and second-degree (menu) pricing Chapter 5: Price Discrimination and Monopoly 4

First-degree price discrimination 2 • Monopolist can charge maximum price that each consumer is willing to pay • Extracts all consumer surplus • Since profit is now total surplus, find that first-degree price discrimination is efficient Chapter 5: Price Discrimination and Monopoly 5

First-degree price discrimination 3 • Suppose that you own five antique cars • Market research shows there are collectors of different types – keenest is willing to pay $10, 000 for a car, second keenest $8, 000, third keenest $6, 000, fourth keenest $4, 000, fifth keenest $2, 000 – sell the first car at $10, 000 – sell the second car at $8, 000 – sell the third car to at $6, 000 and so on – total revenue $30, 000 • Contrast with linear pricing: all cars sold at the same price – set a price of $6, 000 – sell three cars – total revenue $18, 000 Chapter 5: Price Discrimination and Monopoly 6

First-degree price discrimination 4 • First-degree price discrimination is highly profitable but requires – detailed information – ability to avoid arbitrage • Leads to the efficient choice of output: since price equals marginal revenue and MR = MC – no value-creating exchanges are missed Chapter 5: Price Discrimination and Monopoly 7

First-degree price discrimination 5 • The information requirements appear to be insurmountable – but not in particular cases • tax accountants, doctors, students applying to private universities • No arbitrage is less restrictive but potentially a problem • But there are pricing schemes that will achieve the same outcome – non-linear prices – two-part pricing as a particular example of non-linear prices • charge a quantity-independent fee (membership? ) plus a per unit usage charge – block pricing is another • bundle total charge and quantity in a package Chapter 5: Price Discrimination and Monopoly 8

Two-part pricing • Jazz club serves two types of customer – Old: demand for entry plus Qo drinks is P = Vo – Qo – Young: demand for entry plus Qy drinks is P = Vy – Qy – Equal numbers of each type – Assume that Vo > Vy: Old are willing to pay more than Young – Cost of operating the jazz club C(Q) = F + c. Q • Demand costs are all in daily units Chapter 5: Price Discrimination and Monopoly 9

Two-part pricing 2 • Suppose that the jazz club owner applies “traditional” linear pricing: free entry and a set price for drinks – – – – – aggregate demand is Q = Qo + Qy = (Vo + Vy) – 2 P invert to give: P = (Vo + Vy)/2 – Q/2 MR is then MR = (Vo + Vy)/2 – Q equate MR and MC, where MC = c and solve for Q to give QU = (Vo + Vy)/2 – c substitute into aggregate demand to give the equilibrium price PU = (Vo + Vy)/4 + c/2 each Old consumer buys Qo = (3 Vo – Vy)/4 – c/2 drinks each Young consumer buys Qy = (3 Vy – Vo)/4 – c/2 drinks profit from each pair of Old and Young is U = (Vo + Vy – 2 c)2 Chapter 5: Price Discrimination and Monopoly 10

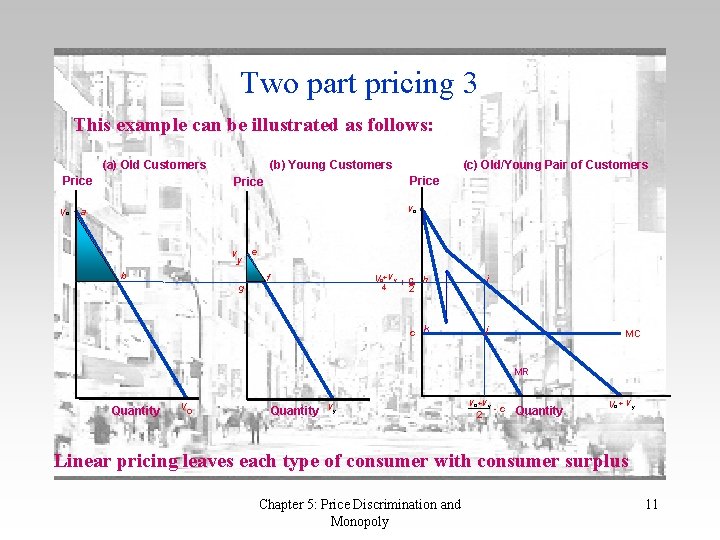
Two part pricing 3 This example can be illustrated as follows: (a) Old Customers Price Vo (b) Young Customers Price Vo a V d (c) Old/Young Pair of Customers y b g e f Vo+V y + c h 4 2 i c k j MC MR Quantity Vo Quantity Vy Vo+V y 2 -c Quantity Vo + Vy Linear pricing leaves each type of consumer with consumer surplus Chapter 5: Price Discrimination and Monopoly 11

Two part pricing 4 • Jazz club owner can do better than this • Consumer surplus at the uniform linear price is: – Old: CSo = (Vo – PU). Qo/2 = (Qo)2/2 – Young: CSy = (Vy – PU). Qy/2 = (Qy)2/2 • So charge an entry fee (just less than): – Eo = CSo to each Old customer and Ey = CSy to each Young customer • check IDs to implement this policy – each type will still be willing to frequent the club and buy the equilibrium number of drinks • So this increases profit by Eo for each Old and Ey for each Young customer Chapter 5: Price Discrimination and Monopoly 12

Two part pricing 5 • The jazz club can do even better – reduce the price per drink – this increases consumer surplus – but the additional consumer surplus can be extracted through a higher entry fee • Consider the best that the jazz club owner can do with respect to each type of consumer Chapter 5: Price Discrimination and Monopoly 13

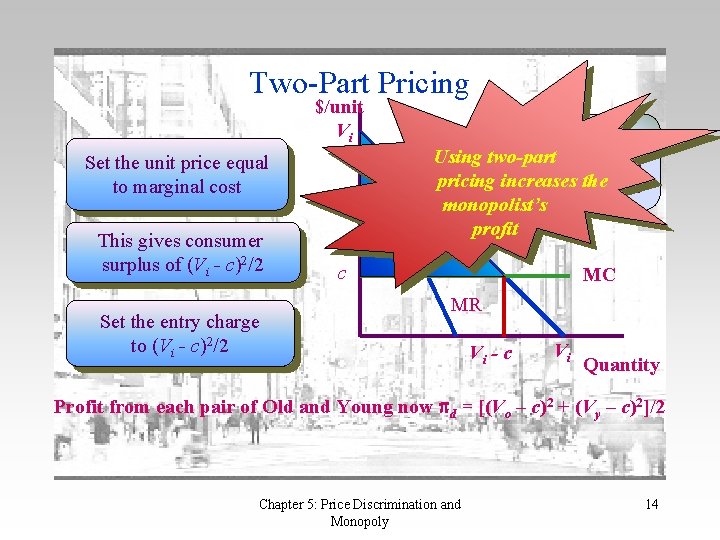
Two-Part Pricing $/unit Vi Set the unit price equal to marginal cost This gives consumer surplus of (Vi - c)2/2 Set the entry charge to (Vi - c)2/2 The entry charge Using two-part converts consumer pricing surplus increases the into profit monopolist’s profit c MC MR Vi - c Vi Quantity Profit from each pair of Old and Young now d = [(Vo – c)2 + (Vy – c)2]/2 Chapter 5: Price Discrimination and Monopoly 14

Block pricing • There is another pricing method that the club owner can apply – offer a package of “Entry plus X drinks for $Y” • To maximize profit apply two rules – set the quantity offered to each consumer type equal to the amount that type would buy at price equal to marginal cost – set the total charge for each consumer type to the total willingness to pay for the relevant quantity • Return to the example: Chapter 5: Price Discrimination and Monopoly 15

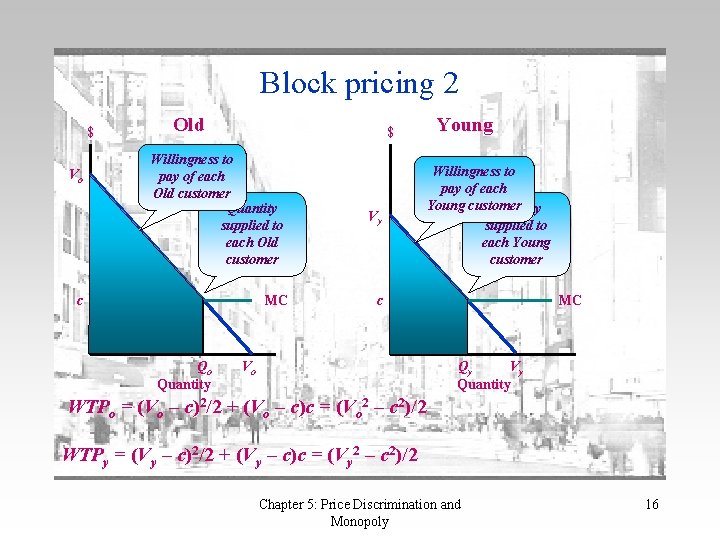
Block pricing 2 $ Vo Old $ Willingness to pay of each Old customer Quantity supplied to each Old customer c MC Qo Quantity Vy Young Willingness to pay of each Young customer Quantity supplied to each Young customer c Vo MC Qy Vy Quantity WTPo = (Vo – c)2/2 + (Vo – c)c = (Vo 2 – c 2)/2 WTPy = (Vy – c)2/2 + (Vy – c)c = (Vy 2 – c 2)/2 Chapter 5: Price Discrimination and Monopoly 16

Block pricing 3 • How to implement this policy? – card at the door – give customers the requisite number of tokens that are exchanged for drinks Chapter 5: Price Discrimination and Monopoly 17

A final comment • One final point – average price that is paid by an Old customer = (Vo 2 – c 2)/2(Vo – c) = (Vo + c)/2 – average price paid by a Young customer = (Vy 2 – c 2)/2(Vo – c) = (Vy + c)/2 – identical to the third-degree price discrimination (linear) prices – but the profit outcome is much better with first-degree price discrimination. Why? • consumer equates MC of last unit bought with marginal benefit • with linear pricing MC = AC (= average price) • with first-degree price discrimination MC of last unit bought is less than AC (= average price) so more is bought Chapter 5: Price Discrimination and Monopoly 18

Third-degree price discrimination • Consumers differ by some observable characteristic(s) • A uniform price is charged to all consumers in a particular group – linear price • Different uniform prices are charged to different groups – “kids are free” – subscriptions to professional journals e. g. American Economic Review – airlines • the number of different economy fares charged can be very large indeed! – early-bird specials; first-runs of movies Chapter 5: Price Discrimination and Monopoly 19

Third-degree price discrimination 2 • The pricing rule is very simple: – consumers with low elasticity of demand should be charged a high price – consumers with high elasticity of demand should be charged a low price Chapter 5: Price Discrimination and Monopoly 20

Third degree price discrimination: example • Harry Potter volume sold in the United States and Europe • Demand: – United States: PU = 36 – 4 QU – Europe: PE = 24 – 4 QE • Marginal cost constant in each market – MC = $4 Chapter 5: Price Discrimination and Monopoly 21

The example: no price discrimination • Suppose that the same price is charged in both markets • Use the following procedure: – calculate aggregate demand in the two markets – identify marginal revenue for that aggregate demand – equate marginal revenue with marginal cost to identify the profit maximizing quantity – identify the market clearing price from the aggregate demand – calculate demands in the individual markets from the individual market demand curves and the equilibrium price Chapter 5: Price Discrimination and Monopoly 22

The example (npd cont. ) United States: PU = 36 – 4 QU Invert this: QU = 9 – P/4 for P < $36 Europe: PU = 24 – 4 QE Invert QE = 6 – P/4 for P < $24 Aggregate these demands Q = QU + QE = 9 – P/4 for $36 < P < Q = QU + QE = 15 – P/2 for P < $24 Chapter 5: Price Discrimination and Monopoly At these prices only the US market is active Now both markets are $24 active 23

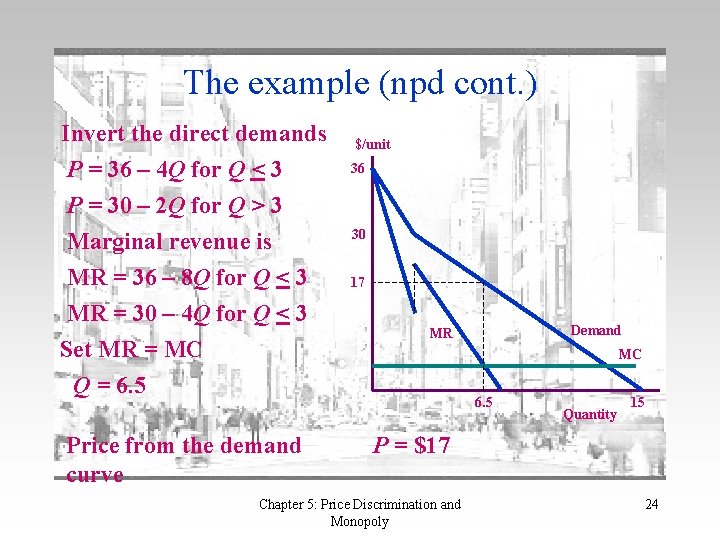
The example (npd cont. ) Invert the direct demands P = 36 – 4 Q for Q < 3 P = 30 – 2 Q for Q > 3 Marginal revenue is MR = 36 – 8 Q for Q < 3 MR = 30 – 4 Q for Q < 3 Set MR = MC Q = 6. 5 Price from the demand curve $/unit 36 30 17 Demand MR MC 6. 5 Quantity 15 P = $17 Chapter 5: Price Discrimination and Monopoly 24

The example (npd cont. ) Substitute price into the individual market demand curves: QU = 9 – P/4 = 9 – 17/4 = 4. 75 million QE = 6 – P/4 = 6 – 17/4 = 1. 75 million Aggregate profit = (17 – 4)x 6. 5 = $84. 5 million Chapter 5: Price Discrimination and Monopoly 25

The example: price discrimination • The firm can improve on this outcome • Check that MR is not equal to MC in both markets – MR > MC in Europe – MR < MC in the US – the firms should transfer some books from the US to Europe • This requires that different prices be charged in the two markets • Procedure: – take each market separately – identify equilibrium quantity in each market by equating MR and MC – identify the price in each market from market demand Chapter 5: Price Discrimination and Monopoly 26

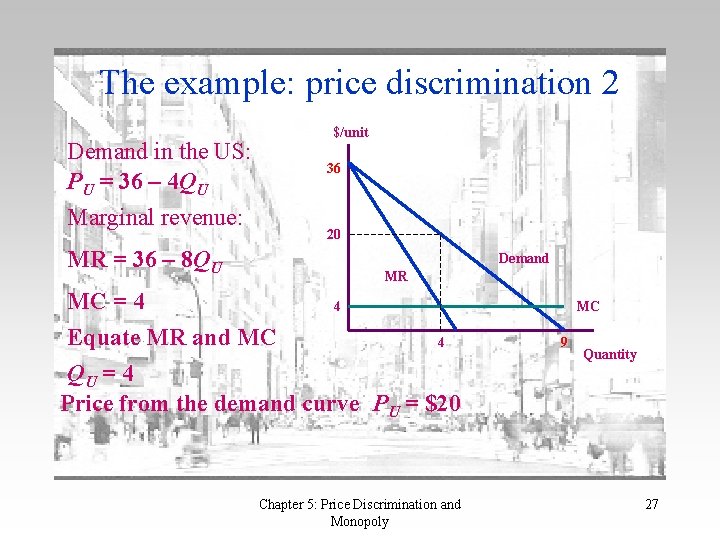
The example: price discrimination 2 Demand in the US: PU = 36 – 4 QU Marginal revenue: MR = 36 – 8 QU $/unit 36 20 Demand MR MC = 4 4 Equate MR and MC 4 QU = 4 Price from the demand curve PU = $20 Chapter 5: Price Discrimination and Monopoly MC 9 Quantity 27

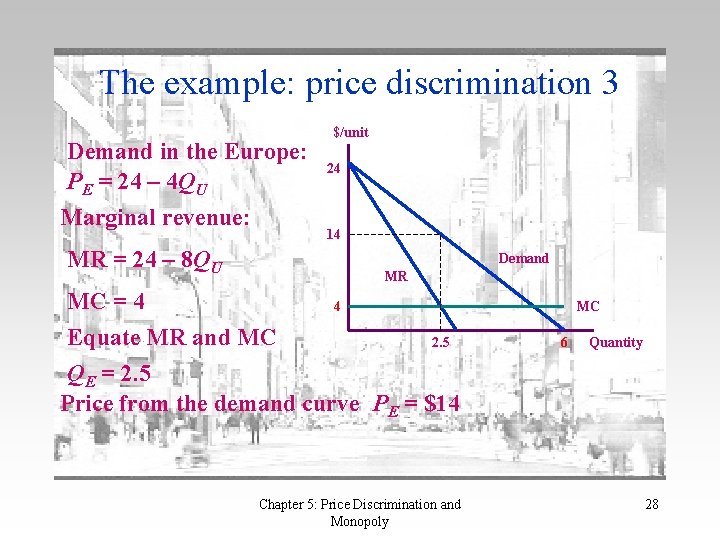
The example: price discrimination 3 Demand in the Europe: PE = 24 – 4 QU Marginal revenue: MR = 24 – 8 QU $/unit 24 14 Demand MR MC = 4 4 Equate MR and MC 2. 5 QE = 2. 5 Price from the demand curve PE = $14 Chapter 5: Price Discrimination and Monopoly MC 6 Quantity 28

The example: price discrimination 4 • Aggregate sales are 6. 5 million books – the same as without price discrimination • Aggregate profit is (20 – 4)x 4 + (14 – 4)x 2. 5 = $89 million – $4. 5 million greater than without price discrimination Chapter 5: Price Discrimination and Monopoly 29

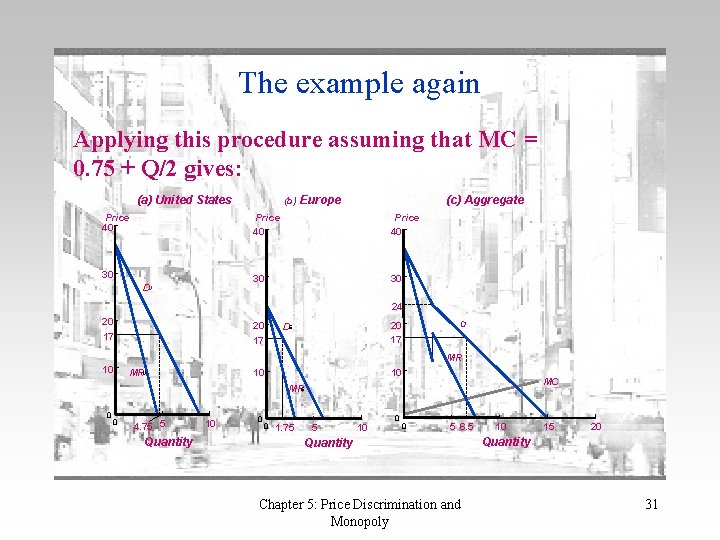
No price discrimination: non-constant cost • The example assumes constant marginal cost • How is this affected if MC is non-constant? – Suppose MC is increasing • No price discrimination procedure – – – Calculate aggregate demand Calculate the associated MR Equate MR with MC to give aggregate output Identify price from aggregate demand Identify market demands from individual demand curves Chapter 5: Price Discrimination and Monopoly 30

The example again Applying this procedure assuming that MC = 0. 75 + Q/2 gives: (a) United States Price 40 30 DU (c) Aggregate (b) Europe Price 40 30 30 24 20 17 DE MR 10 MRU 10 10 MC MRE 0 0 4. 75 5 Quantity 10 0 0 1. 75 5 10 0 0 5 6. 5 Quantity Chapter 5: Price Discrimination and Monopoly 10 15 20 Quantity 31

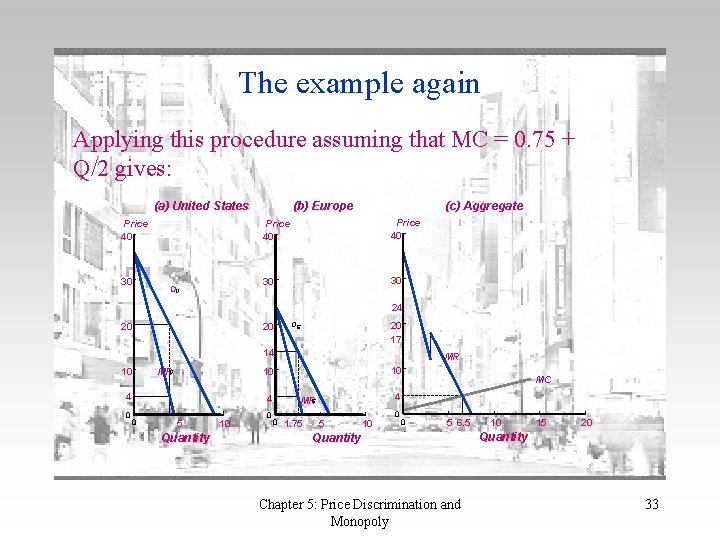
Price discrimination: non-constant cost • With price discrimination the procedure is – Identify marginal revenue in each market – Aggregate these marginal revenues to give aggregate marginal revenue – Equate this MR with MC to give aggregate output – Identify equilibrium MR from the aggregate MR curve – Equate this MR with MC in each market to give individual market quantities – Identify equilibrium prices from individual market demands Chapter 5: Price Discrimination and Monopoly 32

The example again Applying this procedure assuming that MC = 0. 75 + Q/2 gives: (a) United States Price 40 30 DU (c) Aggregate (b) Europe Price 40 30 30 24 20 20 20 17 DE 14 10 4 0 MR 10 10 MRU 5 Quantity 10 0 4 MRE 0 1. 75 MC 5 10 0 0 5 6. 5 Quantity Chapter 5: Price Discrimination and Monopoly 10 15 20 Quantity 33

Some additional comments • Suppose that demands are linear – price discrimination results in the same aggregate output as no price discrimination – price discrimination increases profit • For any demand specifications two rules apply – marginal revenue must be equalized in each market – marginal revenue must equal aggregate marginal cost Chapter 5: Price Discrimination and Monopoly 34

Price discrimination and elasticity • Suppose that there are two markets with the same MC • MR in market i is given by MRi = Pi(1 – 1/ i) – where i is (absolute value of) elasticity of demand • From rule 1 (above) – MR 1 = MR 2 – so P 1(1 – 1/ 1) = P 2(1 – 1/ 2) which gives P 1 P 2 = (1 – 1/ 2) (1 – 1/ 1) = Price is lower in the market with the higher demand elasticity 1 2 – 1 1 2 – 2 Chapter 5: Price Discrimination and Monopoly 35

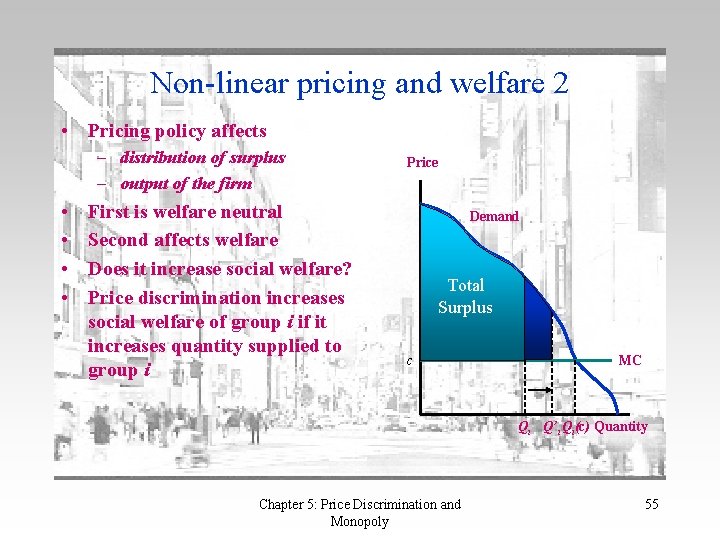
Third-degree price discrimination and welfare • Does third-degree price discrimination reduce welfare? – not the same as being “fair” – relates solely to efficiency – so consider impact on total surplus Chapter 5: Price Discrimination and Monopoly 36

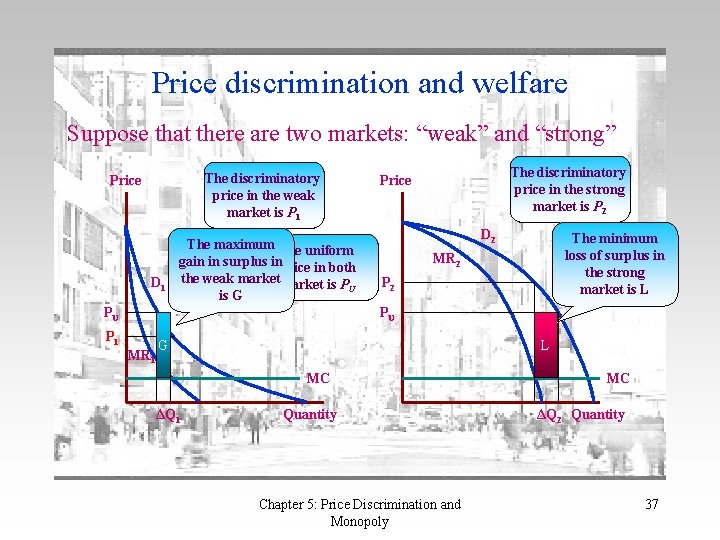
Price discrimination and welfare Suppose that there are two markets: “weak” and “strong” The discriminatory price in the weak market is P 1 Price D 1 The maximum The uniform gain in surplus inprice in both the weak market is P U is G PU The discriminatory price in the strong market is P 2 Price D 2 The minimum loss of surplus in the strong market is L MR 2 PU P 1 MR 1 G L MC ΔQ 1 Quantity Chapter 5: Price Discrimination and Monopoly MC ΔQ 2 Quantity 37

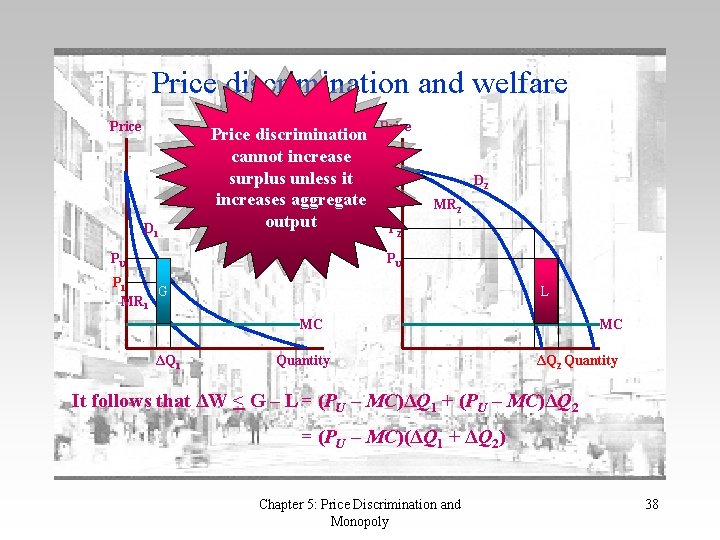
Price discrimination and welfare Price D 1 Price discrimination cannot increase surplus unless it increases aggregate output PU Price D 2 MR 2 PU P 1 G MR 1 L MC ΔQ 1 Quantity MC ΔQ 2 Quantity It follows that ΔW < G – L = (PU – MC)ΔQ 1 + (PU – MC)ΔQ 2 = (PU – MC)(ΔQ 1 + ΔQ 2) Chapter 5: Price Discrimination and Monopoly 38

Price discrimination and welfare 2 • Previous analysis assumes that the same markets are served with and without price discrimination • This may not be true – uniform price is affected by demand in “weak” markets – firm may then prefer not to serve such markets without price discrimination – price discrimination may open up weak markets • The result can be an increase in aggregate output and an increase in welfare Chapter 5: Price Discrimination and Monopoly 39

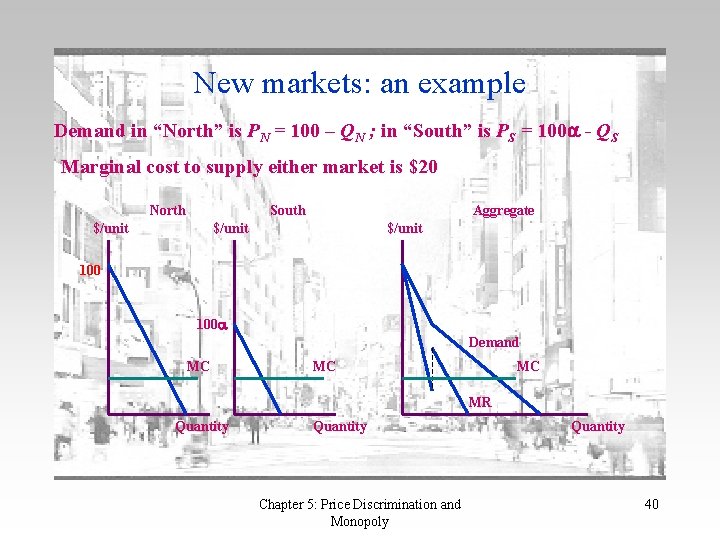
New markets: an example Demand in “North” is PN = 100 – QN ; in “South” is PS = 100 - QS Marginal cost to supply either market is $20 North South $/unit Aggregate $/unit 100 Demand MC MC MC MR Quantity Chapter 5: Price Discrimination and Monopoly Quantity 40

New Markets: the example 2 Aggregate demand is P = (1 + )50 – Q/2 provided that both markets are served $/unit Aggregate Equate MR and MC to get equilibrium output QA = (1 + )50 - 20 Get equilibrium price from aggregate demand P = 35 + 25 P Demand MC MR QA Chapter 5: Price Discrimination and Monopoly Quantity 41

New Markets: the example 3 Aggregate Now consider the impact of a reduction in Aggregate demand changes Marginal revenue changes It is no longer the case that both markets are served $/unit PN Demand MC The South market is dropped Price in North is the monopoly price for that market Chapter 5: Price Discrimination and Monopoly MR MR' D' Quantity 42

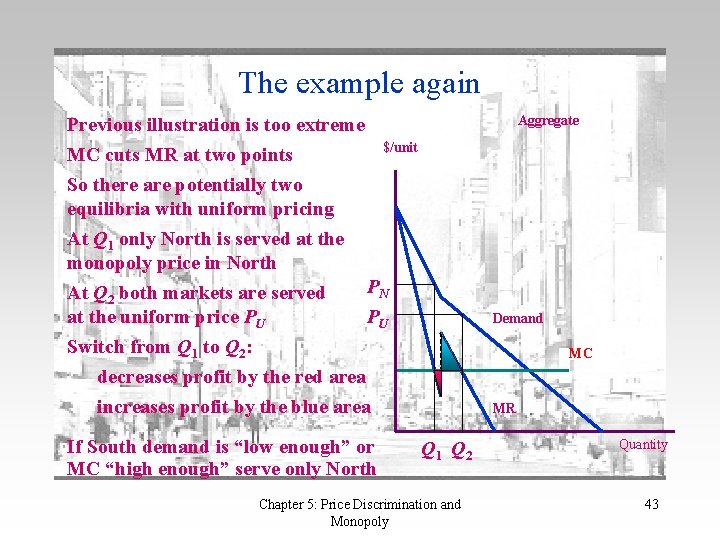
The example again Aggregate Previous illustration is too extreme MC cuts MR at two points So there are potentially two equilibria with uniform pricing At Q 1 only North is served at the monopoly price in North $/unit PN At Q 2 both markets are served at the uniform price PU PU Switch from Q 1 to Q 2: decreases profit by the red area increases profit by the blue area If South demand is “low enough” or MC “high enough” serve only North Demand MC MR Q 1 Q 2 Chapter 5: Price Discrimination and Monopoly Quantity 43

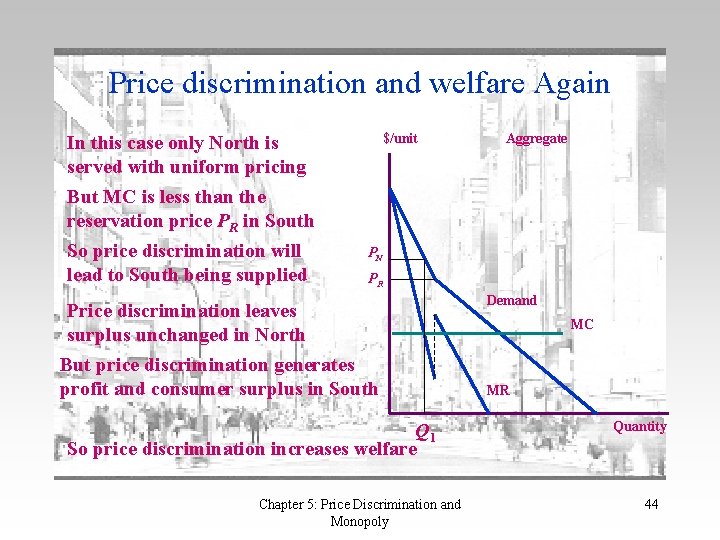
Price discrimination and welfare Again In this case only North is served with uniform pricing But MC is less than the reservation price PR in South So price discrimination will lead to South being supplied $/unit Aggregate PN PR Price discrimination leaves surplus unchanged in North But price discrimination generates profit and consumer surplus in South Q 1 So price discrimination increases welfare Chapter 5: Price Discrimination and Monopoly Demand MC MR Quantity 44

Price discrimination and welfare One more time • Suppose only North is served with a uniform price • Also assume that South will be served with price discrimination – Welfare in North is unaffected – Consumer surplus is created in South: opening of a new market – Profit is generated in South: otherwise the market is not opened • As a result price discrimination increases welfare. Chapter 5: Price Discrimination and Monopoly 45

Second-degree price discrimination • What if the seller cannot distinguish between buyers? – perhaps they differ in income (unobservable) • Then the type of price discrimination just discussed is impossible • High-income buyer will pretend to be a low-income buyer – to avoid the high entry price – to pay the smaller total charge • Take a specific example – Ph = 16 – Qh – Pl = 12 – Ql – MC = 4 Chapter 5: Price Discrimination and Monopoly 46

Second-degree price discrimination 2 • First-degree price discrimination requires: – High Income: entry fee $72 and $4 per drink or entry plus 12 drinks for a total charge of $120 – Low Income: entry fee $32 and $4 per drink or entry plus 8 drinks for total charge of $64 • This will not work – high income types get no consumer surplus from the package designed for them but get consumer surplus from the other package – so they will pretend to be low income even if this limits the number of drinks they can buy • Need to design a “menu” of offerings targeted at the two types Chapter 5: Price Discrimination and Monopoly 47

Second-degree price discrimination 3 • The seller has to compromise • Design a pricing scheme that makes buyers – reveal their true types – self-select the quantity/price package designed for them • Essence of second-degree price discrimination • It is “like” first-degree price discrimination – the seller knows that there are buyers of different types – but the seller is not able to identify the different types • A two-part tariff is ineffective – allows deception by buyers • Use quantity discounting Chapter 5: Price Discrimination and Monopoly 48

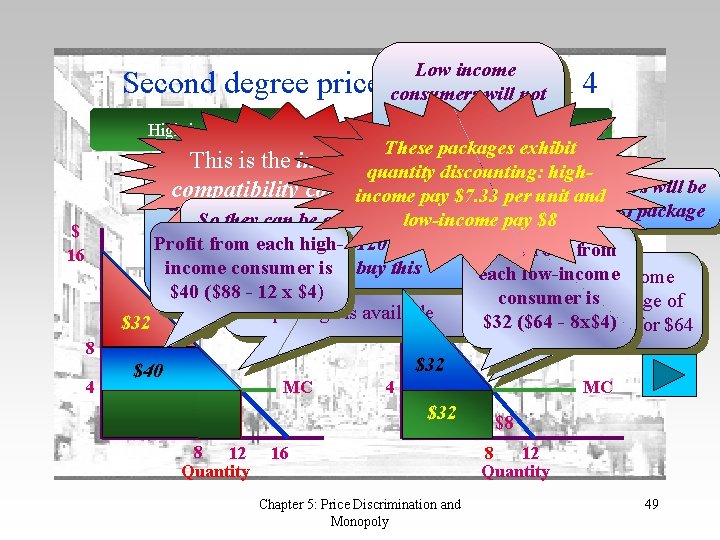
Low income consumers will not buy the ($88, 12) High-income Low-Income package since they These packages exhibit This is the incentive are willing to pay highquantity discounting: So any other package So will the high. The low-demand consumers will be only $72 forper 12 unit compatibility constraint income pay $7. 33 and income consumers: offered to high-income willing to buy this ($64, 8) package drinks low-income pay $8 So they can be offered a package because consumers the ($64, 8) must $ - offer at High income consumers are Profit of from ($88, each 12) (since high$120 32 = 88) And profit from package gives them $32 willing to pay up to $120 for least $32 income consumer and theyconsumer is will buy thissurplus each low-income consumer surplus Offer the low-income 12 entry plus 12 drinks if no other $40 ($88 - 12 x $4) consumer aispackage of consumers package is available $32 entry($64 plus- 88 x$4) drinks for $64 Second degree price discrimination 4 $ 16 8 4 $32 $40 $64 $32 $8 $24 $32 MC $16 8 12 Quantity 4 MC $32 16 Chapter 5: Price Discrimination and Monopoly $8 8 12 Quantity 49

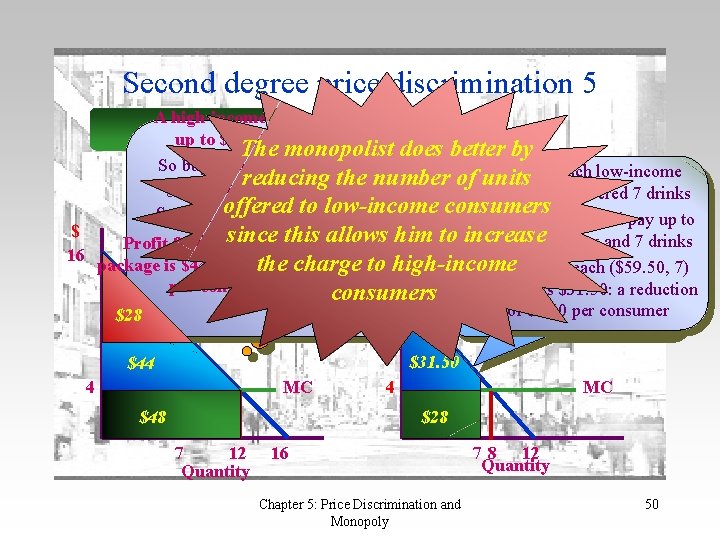
Second degree price discrimination 5 A high-income consumer will pay High-Income up to $87. 50 for entry and 7 The monopolist does better by drinks So buying the ($59. 50, 7) package Suppose each low-income reducing the number of units gives him $28 consumer surplus consumer is offered 7 drinks offered to low-income consumers Can thebeclub. So entry plus 12 drinks can sold Each consumer will pay up to Low-Income for each $92 ($120 -12) 28 allows = $92) since this him to increase owner do $even $59. 50 for entry and 7 drinks Profit from ($92, $ 16 package is $44: an increase of $4 the charge to this? high-income Yes! Reduce the number Profit from each ($59. 50, 7) better than 12 per consumer package is $31. 50: reduction of units offered toaeach consumers of $0. 50 per consumer low-income consumer $28 4 $87. 50 $44$92 MC $28$48 4 $31. 50 $59. 50 MC $28 7 12 Quantity 16 Chapter 5: Price Discrimination and Monopoly 7 8 12 Quantity 50

Second-degree price discrimination 6 • Will the monopolist always want to supply both types of consumer? • There are cases where it is better to supply only highdemand types – high-class restaurants – golf and country clubs • Take our example again – suppose that there are Nl low-income consumers – and Nh high-income consumers Chapter 5: Price Discrimination and Monopoly 51

Second-degree price discrimination 7 • Suppose both types of consumer are served – two packages are offered ($57. 50, 7) aimed at low-income and ($92, 12) aimed at high-income – profit is $31. 50 x. Nl + $44 x. Nh • Now suppose only high-income consumers are served – then a ($120, 12) package can be offered – profit is $72 x. Nh • Is it profitable to serve both types? – Only if $31. 50 x. Nl + $44 x. Nh > $72 x. Nh 31. 50 Nl > 28 Nh This requires that Nh < 31. 50 = 1. 125 Nl 28 There should not be “too high” a fraction of high-demand consumers Chapter 5: Price Discrimination and Monopoly 52

Second-degree price discrimination 8 • Characteristics of second-degree price discrimination – extract all consumer surplus from the lowest-demand group – leave some consumer surplus for other groups • the incentive compatibility constraint – offer less than the socially efficient quantity to all groups other than the highest-demand group – offer quantity-discounting • Second-degree price discrimination converts consumer surplus into profit less effectively than first-degree • Some consumer surplus is left “on the table” in order to induce high-demand groups to buy large quantities Chapter 5: Price Discrimination and Monopoly 53

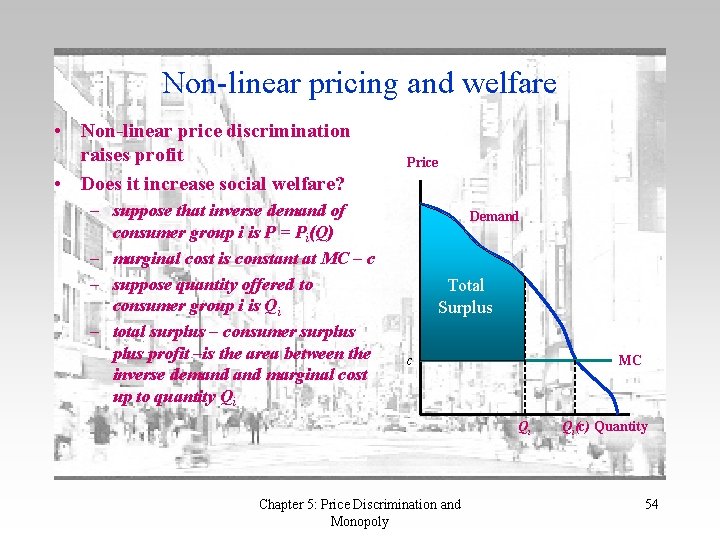
Non-linear pricing and welfare • Non-linear price discrimination raises profit • Does it increase social welfare? – suppose that inverse demand of consumer group i is P = Pi(Q) – marginal cost is constant at MC – c – suppose quantity offered to consumer group i is Qi – total surplus – consumer surplus profit –is the area between the inverse demand marginal cost up to quantity Qi Price Demand Total Surplus c MC Qi Chapter 5: Price Discrimination and Monopoly Qi(c) Quantity 54

Non-linear pricing and welfare 2 • Pricing policy affects – distribution of surplus – output of the firm • • First is welfare neutral Second affects welfare Does it increase social welfare? Price discrimination increases social welfare of group i if it increases quantity supplied to group i Price Demand Total Surplus c MC Qi Q’i Qi(c) Quantity Chapter 5: Price Discrimination and Monopoly 55

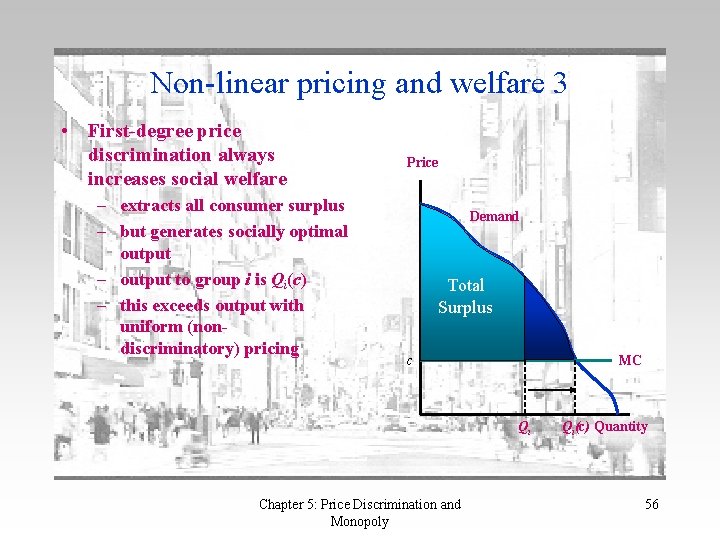
Non-linear pricing and welfare 3 • First-degree price discrimination always increases social welfare – extracts all consumer surplus – but generates socially optimal output – output to group i is Qi(c) – this exceeds output with uniform (nondiscriminatory) pricing Price Demand Total Surplus c MC Qi Chapter 5: Price Discrimination and Monopoly Qi(c) Quantity 56

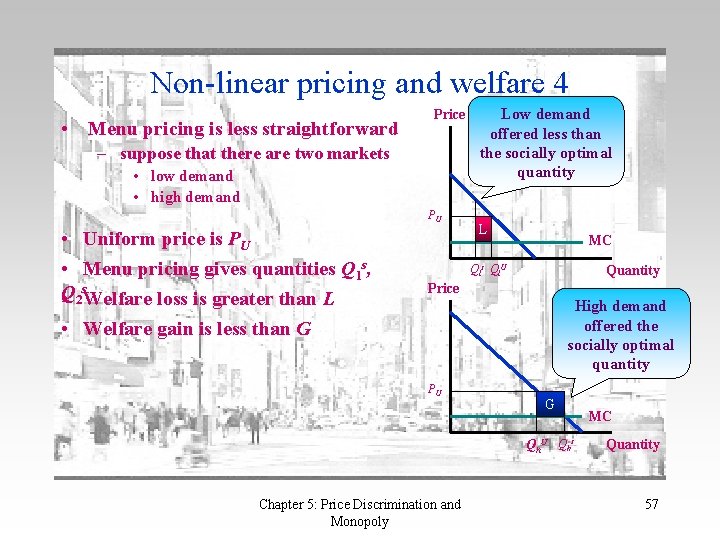
Non-linear pricing and welfare 4 • Menu pricing is less straightforward Price – suppose that there are two markets • low demand • high demand PU • Uniform price is PU • Menu pricing gives quantities Q 1 s, s Q • 2 Welfare loss is greater than L • Welfare gain is less than G Low demand offered less than the socially optimal quantity L MC Qls Ql. U Quantity Price High demand offered the socially optimal quantity PU G Qh. U Qhs Chapter 5: Price Discrimination and Monopoly MC Quantity 57

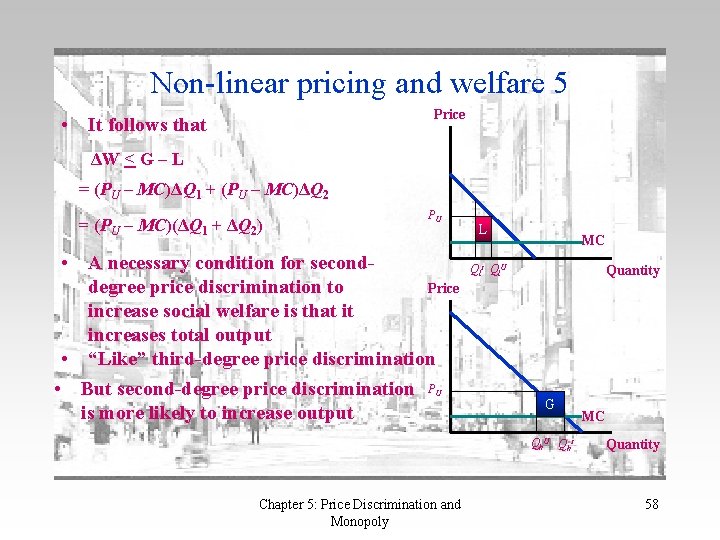
Non-linear pricing and welfare 5 Price • It follows that ΔW < G – L = (PU – MC)ΔQ 1 + (PU – MC)ΔQ 2 = (PU – MC)(ΔQ 1 + ΔQ 2) PU • A necessary condition for seconddegree price discrimination to Price increase social welfare is that it increases total output • “Like” third-degree price discrimination • But second-degree price discrimination P is more likely to increase output U L MC Qls Ql. U Quantity G Qh. U Qhs Chapter 5: Price Discrimination and Monopoly MC Quantity 58

The incentive compatibility constraint • Any offer made to high demand consumers must offer them as much consumer surplus as they would get from an offer designed for low-demand consumers. • This is a common phenomenon – performance bonuses must encourage effort – insurance policies need large deductibles to deter cheating – piece rates in factories have to be accompanied by strict quality inspection – encouragement to buy in bulk must offer a price discount Chapter 5: Price Discrimination and Monopoly 59
 Perfectly price discriminating monopoly
Perfectly price discriminating monopoly Price and output determination under monopoly
Price and output determination under monopoly Kilala ito sa katawagang maximum price policy.
Kilala ito sa katawagang maximum price policy. Socially efficient quantity
Socially efficient quantity Monopoly market examples
Monopoly market examples Monopoly graph deadweight loss
Monopoly graph deadweight loss Monopoly profit maximizing price
Monopoly profit maximizing price Market equilibrium
Market equilibrium Perfectly discriminating monopolist
Perfectly discriminating monopolist Why monopoly arise
Why monopoly arise Perfectly discriminating monopolist
Perfectly discriminating monopolist Perfectly price discriminating monopoly
Perfectly price discriminating monopoly Price determination under monopoly
Price determination under monopoly Single price monopoly graph
Single price monopoly graph Perfect price discrimination คือ
Perfect price discrimination คือ What is first degree price discrimination
What is first degree price discrimination Second degree price discrimination graph
Second degree price discrimination graph Price discrimination occurs when
Price discrimination occurs when Price discrimination real world examples
Price discrimination real world examples Student discount price discrimination
Student discount price discrimination Perfect price discrimination
Perfect price discrimination Objectives of price discrimination
Objectives of price discrimination Versioning price discrimination
Versioning price discrimination Explain price discrimination
Explain price discrimination Hurdle model of price discrimination
Hurdle model of price discrimination Calculus vs algebra
Calculus vs algebra Chapter 16 section 3 segregation and discrimination
Chapter 16 section 3 segregation and discrimination Chapter 8 section 3 segregation and discrimination
Chapter 8 section 3 segregation and discrimination In what regions did the literacy test exist
In what regions did the literacy test exist Government chapter 21 diversity and discrimination
Government chapter 21 diversity and discrimination Monopoly
Monopoly Monopoly market graph
Monopoly market graph Price discovery and price determination
Price discovery and price determination Monopolistic competition pictures
Monopolistic competition pictures Advantages of monopoly
Advantages of monopoly Difference between perfect competition and monopoly market
Difference between perfect competition and monopoly market Example of pure competition
Example of pure competition Difference between perfect competition and monopoly
Difference between perfect competition and monopoly Difference between perfect competition and monopoly market
Difference between perfect competition and monopoly market Product variety and quality under monopoly
Product variety and quality under monopoly P = mc
P = mc Difference between perfect competition and monopoly
Difference between perfect competition and monopoly Product variety and quality under monopoly
Product variety and quality under monopoly Pure competition and monopoly _____
Pure competition and monopoly _____ Marked price-selling price=
Marked price-selling price= Characteristics of hire purchase system
Characteristics of hire purchase system Chain conveyor shot blasting machine
Chain conveyor shot blasting machine Module 77 prejudice and discrimination
Module 77 prejudice and discrimination Discrimination power
Discrimination power Allport's scale diagram
Allport's scale diagram Diversity and discrimination
Diversity and discrimination Merton's typology of prejudice and discrimination
Merton's typology of prejudice and discrimination Jobs for people who stutter
Jobs for people who stutter Serve to a general overall picture of the field of view
Serve to a general overall picture of the field of view Langkah teks eksplanasi
Langkah teks eksplanasi Deadweight loss in a monopoly
Deadweight loss in a monopoly Social cost of monopoly
Social cost of monopoly Monopoly vs perfect competition
Monopoly vs perfect competition Monopoly characteristics
Monopoly characteristics Gilded age entrepreneurs
Gilded age entrepreneurs















































































