Previously you have multiplied algebraic expressions using algebra

Previously, you have multiplied algebraic expressions using algebra tiles and rectangular area models. For example, you may have used an area model to write the product (x + 8)(x + 5) as the sum x 2 + 13 x + 40. Now you will focus on reversing this process: How can you write a product when given a sum? • Warm Up: Reciprocal teaching

4. 1. 1 Introduction to Factoring Expressions October 28, 2019

Objectives • CO: SWBAT use algebra tiles and area models to multiply and factor. • LO: SWBAT identify patterns for determining the dimensions of a completed area model.

Investigate this question by using algebra tiles to build rectangles for the following expressions. For each expression, write an equation showing that the area as a sum equals the area as a product. If you cannot build a rectangle, be prepared to convince the class that no rectangle exists (and thus the expression cannot be factored). 1 a. 2 x 2 + 7 x + 6 =(2 x + 3)(x + 2) 2 + 7 x + 2 b. 6 x 2 =(2 x + 1)(3 x + 2) 2 + 4 x + 1 c. x 3 Not factorable 2 + 3 y d. 2 xy + 6 x + y 4 =(2 x + y)(y + 3) Build, answer, share 4 -2. The process of changing a sum to a product is called factoring. When an expression is written as a product, it is said to be in factored form, and each of the expressions being multiplied is called a factor. Can every expression be factored? That is, can you rewrite every sum as a product?

4 -3. Work with your team to write the sum and the product for the following area models. Are there any special strategies you discovered that can help you determine the dimensions of the rectangle? Be sure to share these strategies with your team. • team

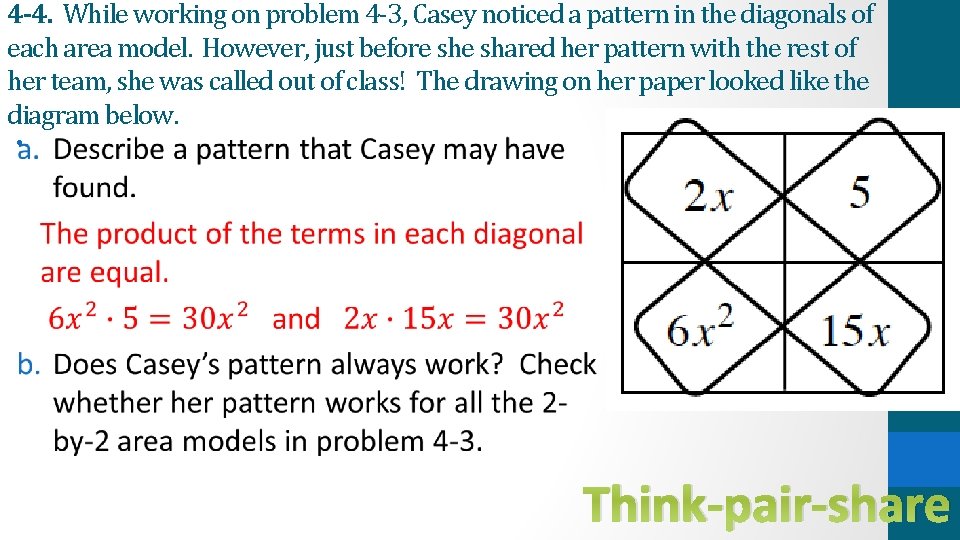
4 -4. While working on problem 4 -3, Casey noticed a pattern in the diagonals of each area model. However, just before shared her pattern with the rest of her team, she was called out of class! The drawing on her paper looked like the diagram below. • Think-pair-share

4 -5. LEARNING LOG – Diagonals of an Area Model Describe Casey’s pattern for the diagonals of a 2 -by-2 area model in your Learning Log. Be sure to include an example. The product of one diagonal in a 2 -by-2 area model always equals the product of the other.