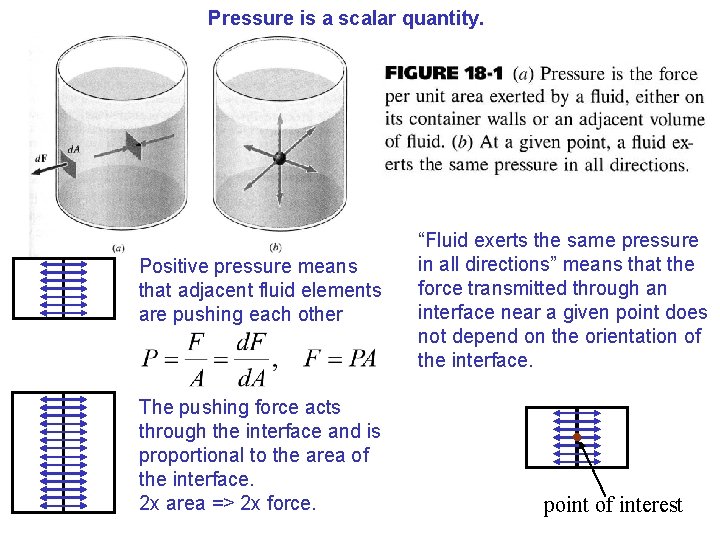
Pressure is a scalar quantity Positive pressure means

Pressure is a scalar quantity. Positive pressure means that adjacent fluid elements are pushing each other The pushing force acts through the interface and is proportional to the area of the interface. 2 x area => 2 x force. “Fluid exerts the same pressure in all directions” means that the force transmitted through an interface near a given point does not depend on the orientation of the interface. point of interest

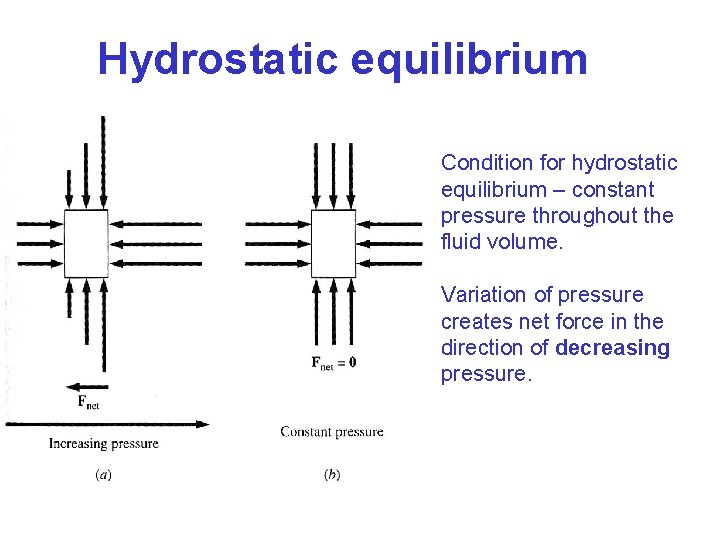
Hydrostatic equilibrium Condition for hydrostatic equilibrium – constant pressure throughout the fluid volume. Variation of pressure creates net force in the direction of decreasing pressure.

Hydrostatic equilibrium with external forces: Gravity Force from above (pushing down) Force from below (pushing up) Gravitational force (pulling down) Balance (equilibrium) equation

Hydrostatic equilibrium with external forces: Gravity We have got a differential equation… Where do we go from here? We need to integrate it. Can we? If both r and g are constant, certainly yes. What is P 0? And BTW, what is h? P 0 is the constant of integration – the value of pressure at h = 0. It is natural to count h downwards from the fluid surface (h = depth). Then P 0 is the pressure at the surface – the atmospheric pressure. If the atmospheric pressure changes, does the pressure at a given depth change? Yep!

If the atmospheric pressure changes, the pressure at all depths changes accordingly. Pascal’s law: a pressure change anywhere in a fluid is felt throughout the fluid. How can we find the pressure inside a closed vessel? We need to know the pressure P 0 at some point. Then to calculate the pressure everywhere else we use Only applicable in the hydrostatic equilibrium.

Hydrostatic equilibrium with external forces: Gravity What is the depth, h, where P = 2 P 0? The density, r, is only constant in liquids. Gasses are compressible, and one must assume variable r(h). Earth atmosphere:

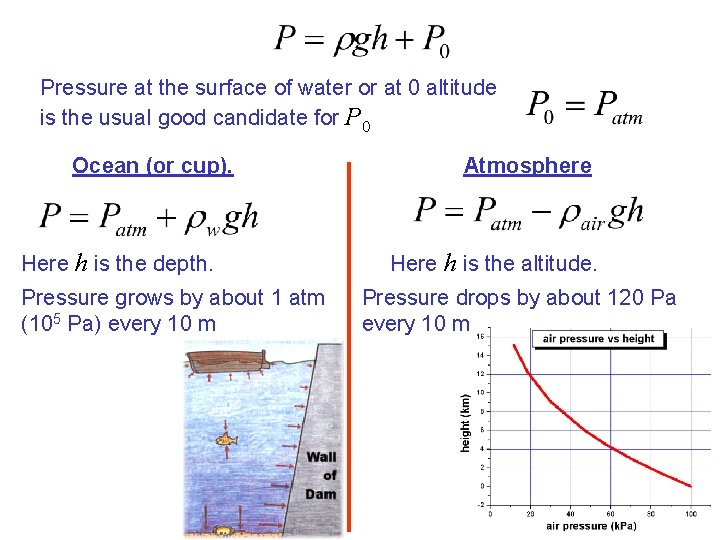
Pressure at the surface of water or at 0 altitude is the usual good candidate for P 0 Ocean (or cup). Here h is the depth. Pressure grows by about 1 atm (105 Pa) every 10 m Atmosphere Here h is the altitude. Pressure drops by about 120 Pa every 10 m

Drinking through a straw. When you get a tooth extracted you are warned not to drink through a straw. Why so? The pressure of liquid at the top of the straw is For you to drink, the pressure inside your mouth should drop below Ptop. This implies a substantial negative pressure difference, rgh, between the blood vessels in your gums and your mouth, which may open the wound.

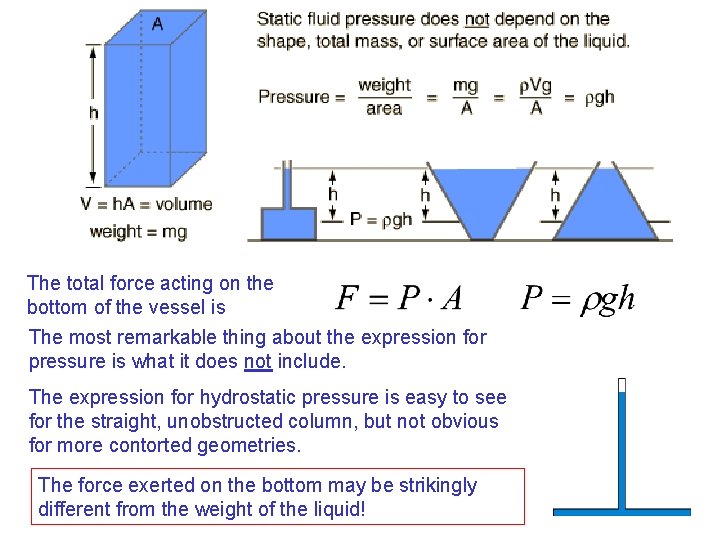
The total force acting on the bottom of the vessel is The most remarkable thing about the expression for pressure is what it does not include. The expression for hydrostatic pressure is easy to see for the straight, unobstructed column, but not obvious for more contorted geometries. The force exerted on the bottom may be strikingly different from the weight of the liquid!

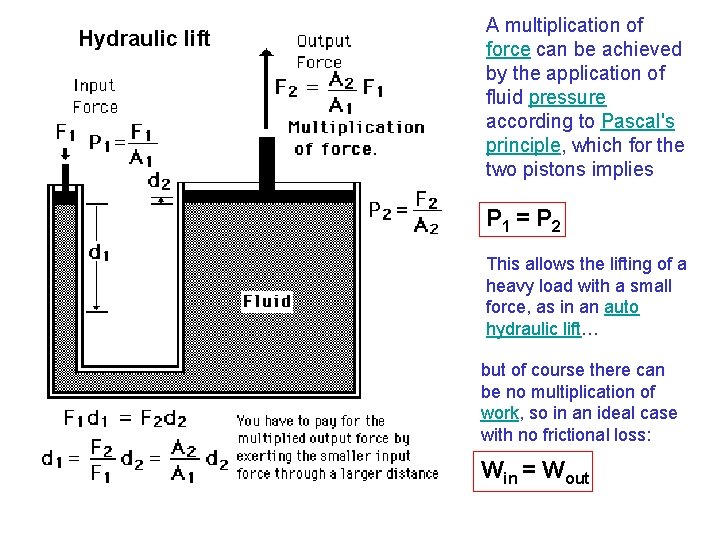
Hydraulic lift A multiplication of force can be achieved by the application of fluid pressure according to Pascal's principle, which for the two pistons implies P 1 = P 2 This allows the lifting of a heavy load with a small force, as in an auto hydraulic lift… but of course there can be no multiplication of work, so in an ideal case with no frictional loss: Win = Wout

A vacuum cleaner Does the vacuum suck the dust? Strictly speaking the pump of the cleaner creates lower pressure inside it and the air and dust are driven into the hose by the pressure of the atmosphere.

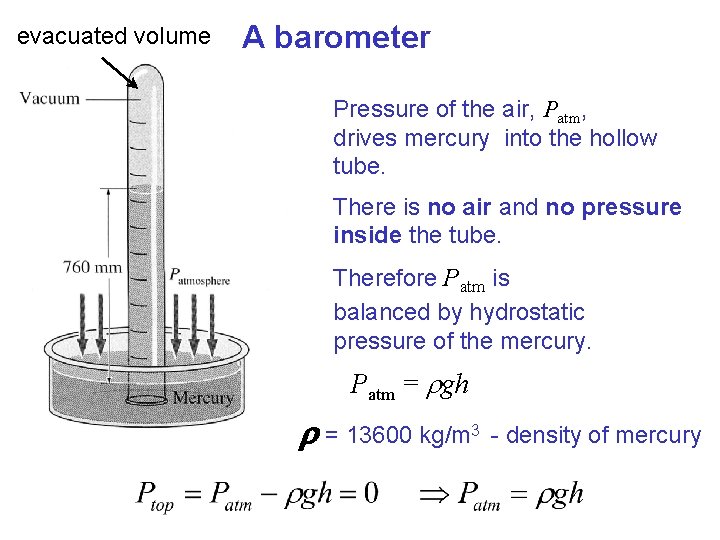
evacuated volume A barometer Pressure of the air, Patm, drives mercury into the hollow tube. There is no air and no pressure inside the tube. Therefore Patm is balanced by hydrostatic pressure of the mercury. Patm = rgh r = 13600 kg/m 3 - density of mercury

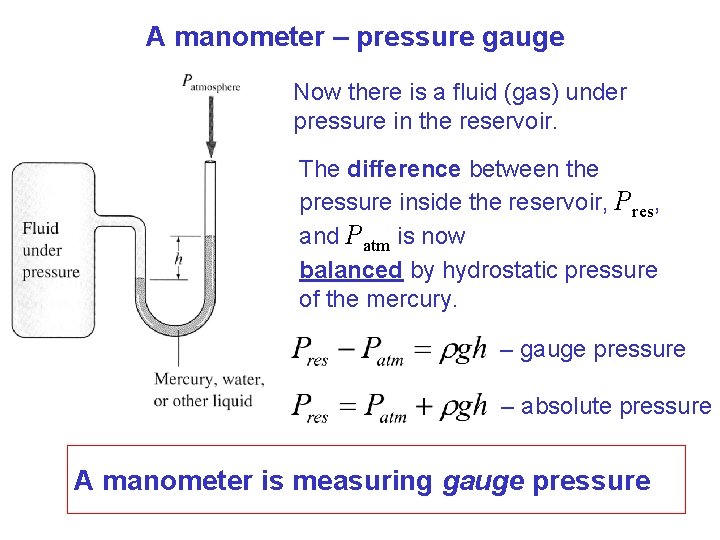
A manometer – pressure gauge Now there is a fluid (gas) under pressure in the reservoir. The difference between the pressure inside the reservoir, Pres, and Patm is now balanced by hydrostatic pressure of the mercury. – gauge pressure – absolute pressure A manometer is measuring gauge pressure

Buoyant force Archimede’s principle: The buoyant force on an object is equal to the weight of the fluid displaced by the object. The buoyant force is applied to the center of gravity of the fluid (center of the submerged volume of the body).