Pressure Drag and Lift for Uniform Flow Over

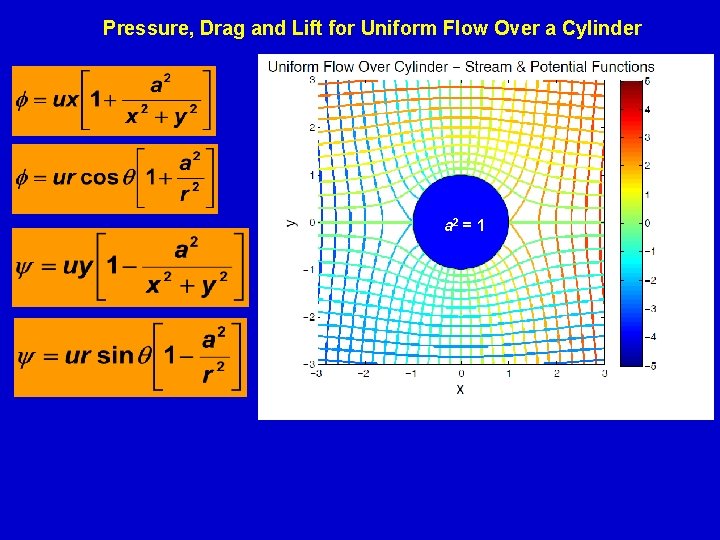
Pressure, Drag and Lift for Uniform Flow Over a Cylinder a 2 = 1

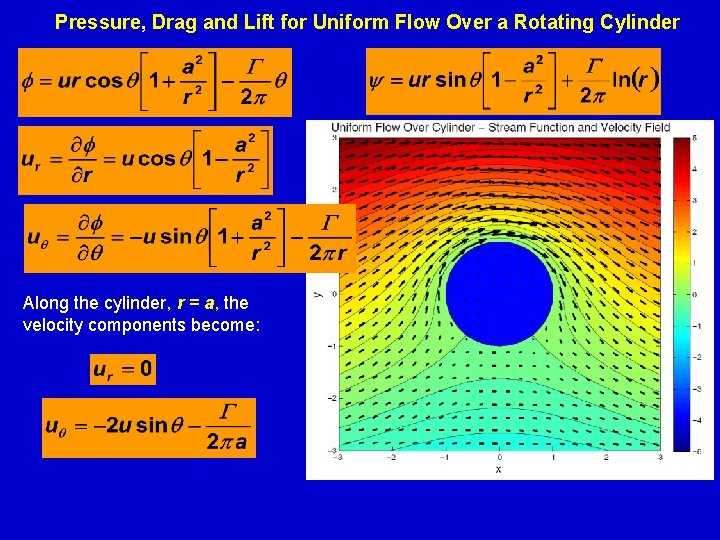
Pressure, Drag and Lift for Uniform Flow Over a Cylinder Along the cylinder, r = a, the velocity components become: uθ is maximum at θ = π/2 and 3 π /2; zero at θ = 0 and θ = π

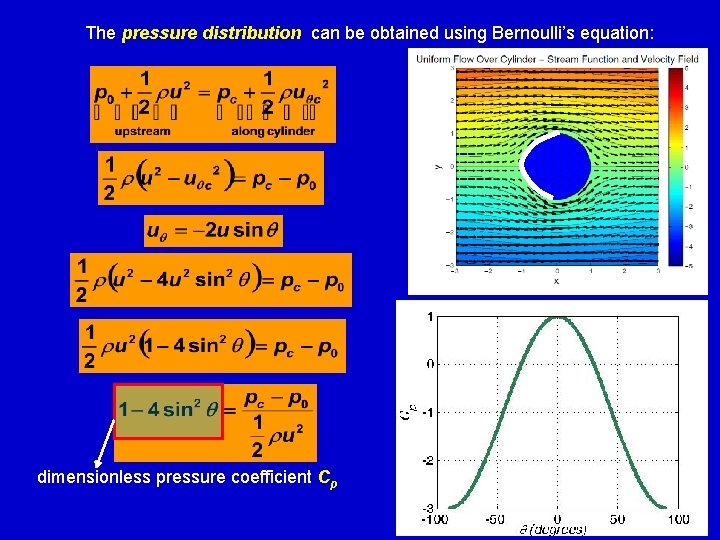
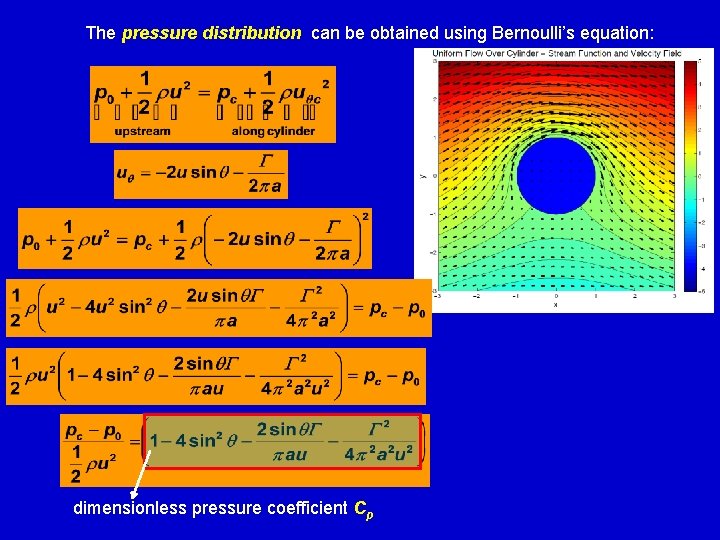
The pressure distribution can be obtained using Bernoulli’s equation: dimensionless pressure coefficient Cp

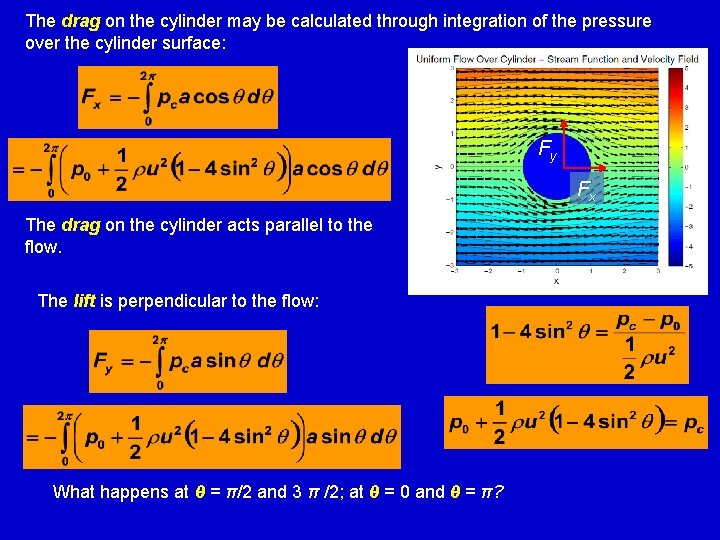
The drag on the cylinder may be calculated through integration of the pressure over the cylinder surface: Fy Fx The drag on the cylinder acts parallel to the flow. The lift is perpendicular to the flow: What happens at θ = π/2 and 3 π /2; at θ = 0 and θ = π?

Pressure, Drag and Lift for Uniform Flow Over a Rotating Cylinder Along the cylinder, r = a, the velocity components become:

The pressure distribution can be obtained using Bernoulli’s equation: dimensionless pressure coefficient Cp

The drag and lift can be obtained by integrating the pressure over the cylinder surface pc : Still no drag for a rotating cylinder There is lift proportional to density, upstream velocity, and strength of vortex -- Kutta – Jukowski law Lifting effect for rotating bodies in a free stream is called Magnus effect

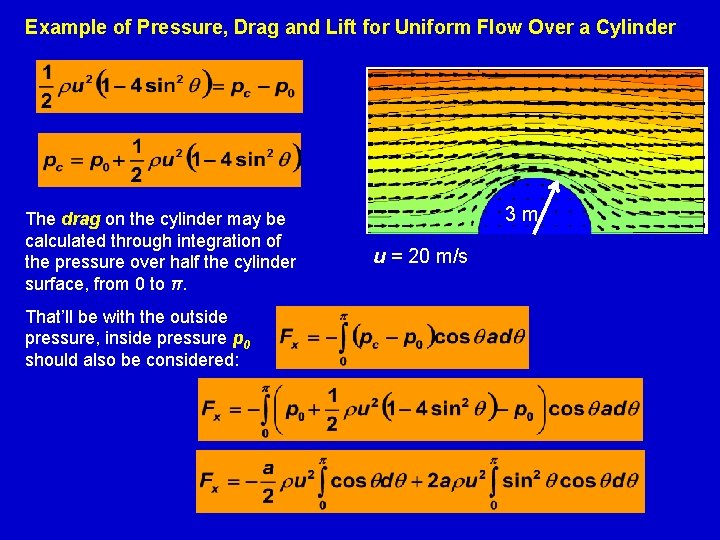
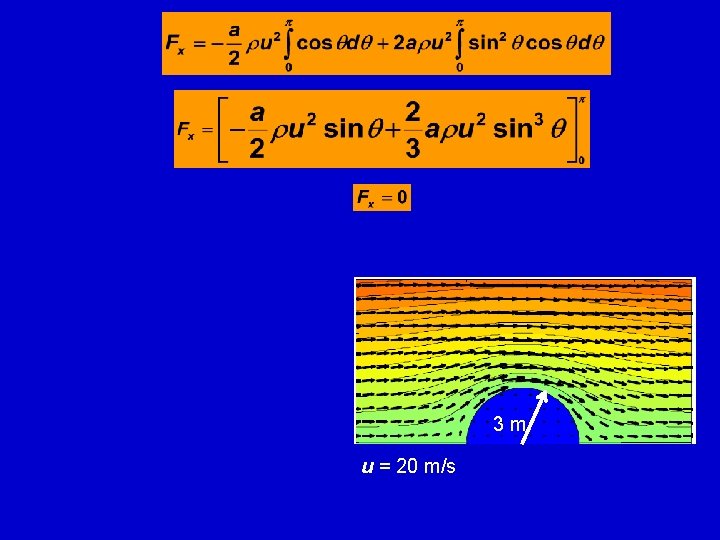
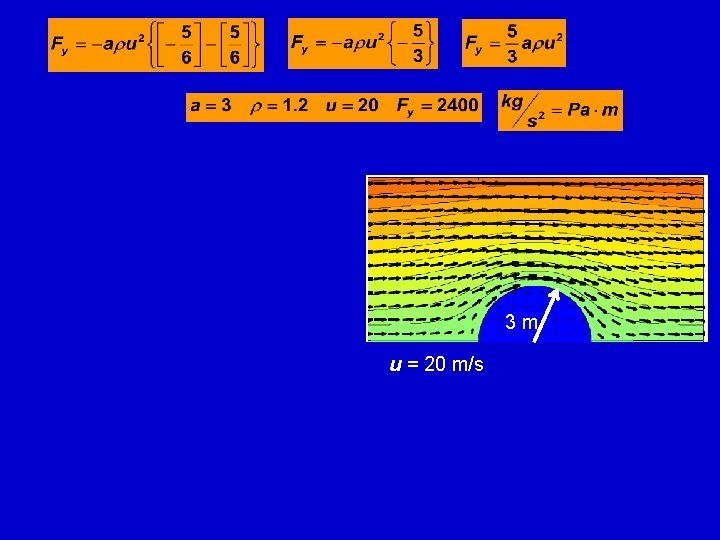
Example of Pressure, Drag and Lift for Uniform Flow Over a Cylinder The drag on the cylinder may be calculated through integration of the pressure over half the cylinder surface, from 0 to π. That’ll be with the outside pressure, inside pressure p 0 should also be considered: 3 m u = 20 m/s

3 m u = 20 m/s

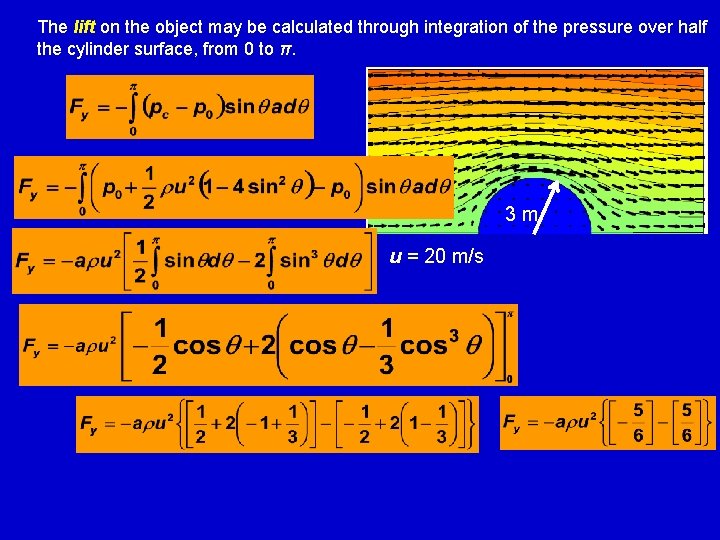
The lift on the object may be calculated through integration of the pressure over half the cylinder surface, from 0 to π. 3 m u = 20 m/s

3 m u = 20 m/s

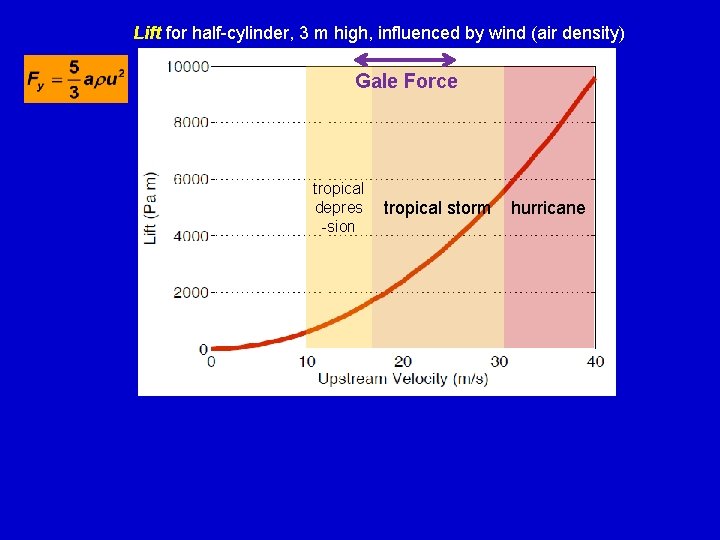
Lift for half-cylinder, 3 m high, influenced by wind (air density) Gale Force tropical depres -sion tropical storm hurricane

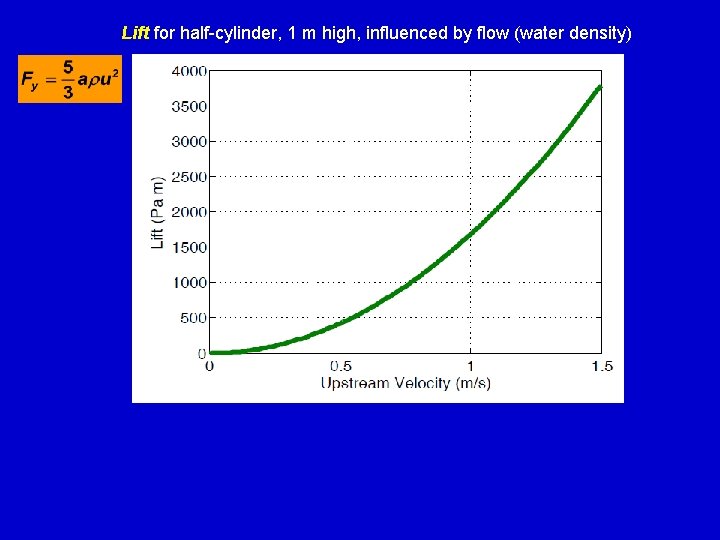
Lift for half-cylinder, 1 m high, influenced by flow (water density)