Presented at the Alabany Chapter of the ASA

Presented at the Alabany Chapter of the ASA February 25, 2004 Washinghton DC
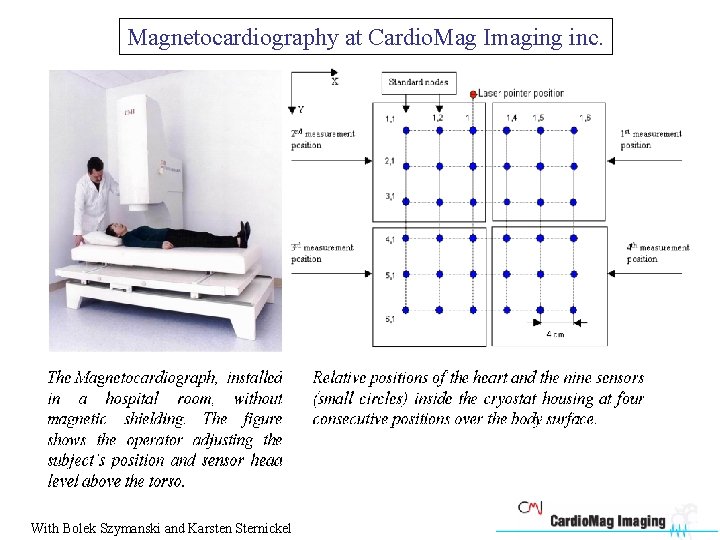
Magnetocardiography at Cardio. Mag Imaging inc. With Bolek Szymanski and Karsten Sternickel
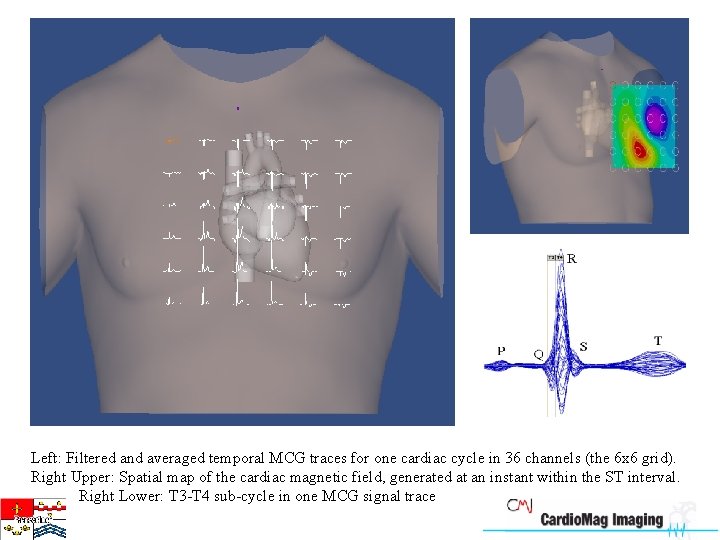
Left: Filtered and averaged temporal MCG traces for one cardiac cycle in 36 channels (the 6 x 6 grid). Right Upper: Spatial map of the cardiac magnetic field, generated at an instant within the ST interval. Right Lower: T 3 -T 4 sub-cycle in one MCG signal trace
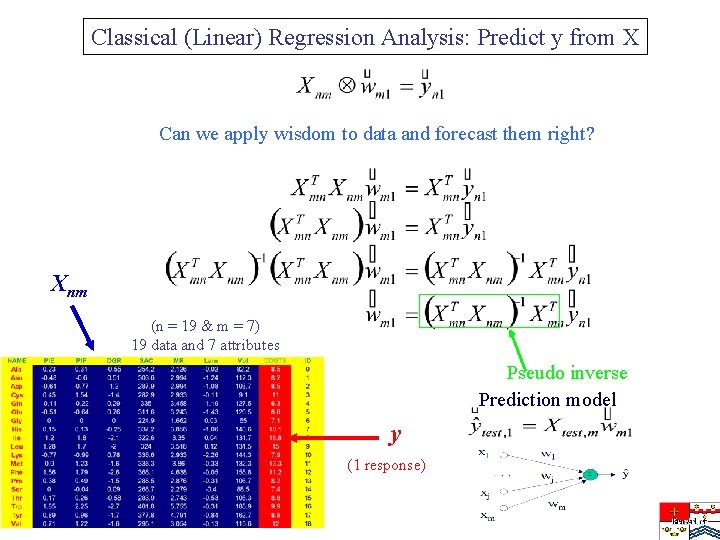
Classical (Linear) Regression Analysis: Predict y from X Can we apply wisdom to data and forecast them right? Xnm (n = 19 & m = 7) 19 data and 7 attributes Pseudo inverse Prediction model y (1 response)

Fundamental Machine Learning Paradox • Learning occurs because of redundancy (patterns) in the data • Machine Learning Paradox: If data contain redundancies (i) we can learn from data (ii) the “feature kernel matrix” KF is ill-conditioned • How to resolve Machine Learning Paradox? (i) fix rank deficiency of KF with principal components (PCA) (ii) regularization: use KF+ I instead of KF (ridge regression) (iii) local learning

Principal Component Regression (PCR): Replace Xnm by Tnh principal components projection of the (n) data records on the (h) “most important” eigenvectors of the feature kernel KF
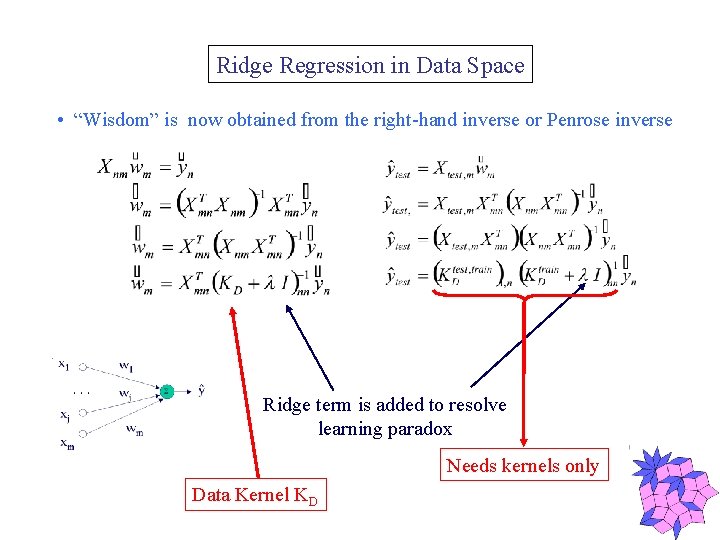
Ridge Regression in Data Space • “Wisdom” is now obtained from the right-hand inverse or Penrose inverse Ridge term is added to resolve learning paradox Needs kernels only Data Kernel KD
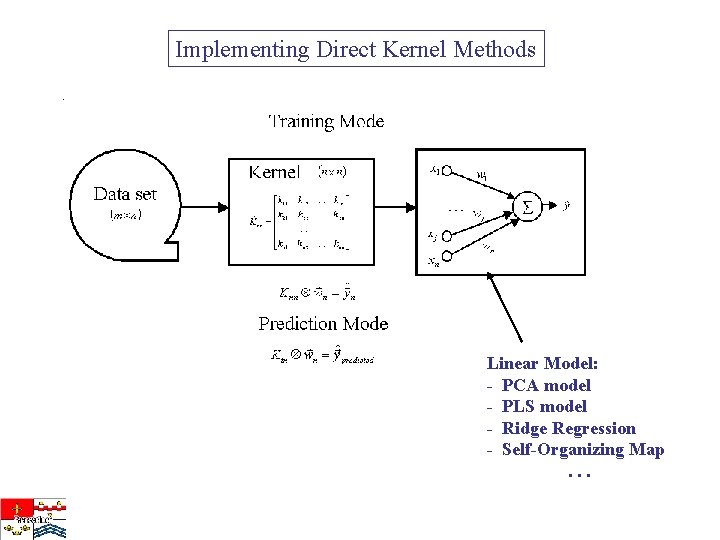
Implementing Direct Kernel Methods Linear Model: - PCA model - PLS model - Ridge Regression - Self-Organizing Map. . .

What have we learned so far? • There is a “learning paradox” because of redundancies in the data • We resolved this paradox by “regularization” - In the case of PCA we used the eigenvectors of the feature kernel - In the case of ridge regression we added a ridge to the data kernel • So far prediction models involved only linear algebra stricly linear • What is in a kernel? xi xj The data kernel contains linear similarity measures (correlations) of data records
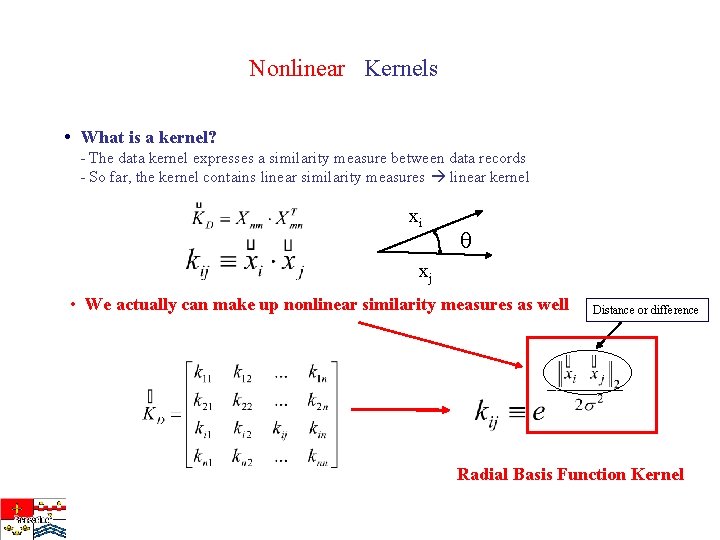
Nonlinear Kernels • What is a kernel? - The data kernel expresses a similarity measure between data records - So far, the kernel contains linear similarity measures linear kernel xi xj • We actually can make up nonlinear similarity measures as well Distance or difference Radial Basis Function Kernel
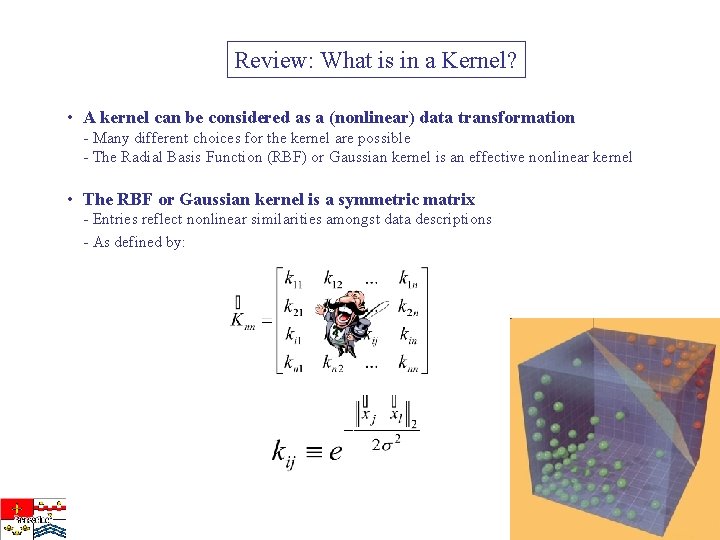
Review: What is in a Kernel? • A kernel can be considered as a (nonlinear) data transformation - Many different choices for the kernel are possible - The Radial Basis Function (RBF) or Gaussian kernel is an effective nonlinear kernel • The RBF or Gaussian kernel is a symmetric matrix - Entries reflect nonlinear similarities amongst data descriptions - As defined by:

Direct Kernel Methods for Nonlinear Regression/Classification • Consider the Kernel as a (nonlinear) data transformation - This is the so-called “kernel trick” (Hilbert, early 1900’s) - The Radial Basis Function (RBF) or Gaussian kernel is an efficient nonlinear kernel • Linear regression models can be “tricked” into nonlinear models by applying such regression models on kernel transformed data - PCA DK-PCA - PLS DK-PLS (Partial Least Squares Support Vector Machines) - (Direct) Kernel Ridge Regression Least Squares Support Vector Machines - Direct Kernel Self-Organizing maps (DK-SOM) • These methods work in the same space as SVMs - DK models can usually be derived also from an optimization formulation (similar to SVMs) - Unlike the original SVMs DK methods are not sparse (i. , e. , all data are support vectors) - Unlike SVMs there is no patent on direct kernel methods - Performance on hunderds of benchmark problems compare favorably with SVMs • Classification can be considered as a special cae of regression • Data Pre-processing: Data are usually Mahalanobis scaled first

Nonlinear PCA in Kernel Space • • Like PCA Consider a nonlinear data kernel transformation up front: Data Kernel Derive principal components for that kernel (e. g. with NIPALS) Examples: - Haykin’s Spiral - Cherkassky’s nonlinear function model
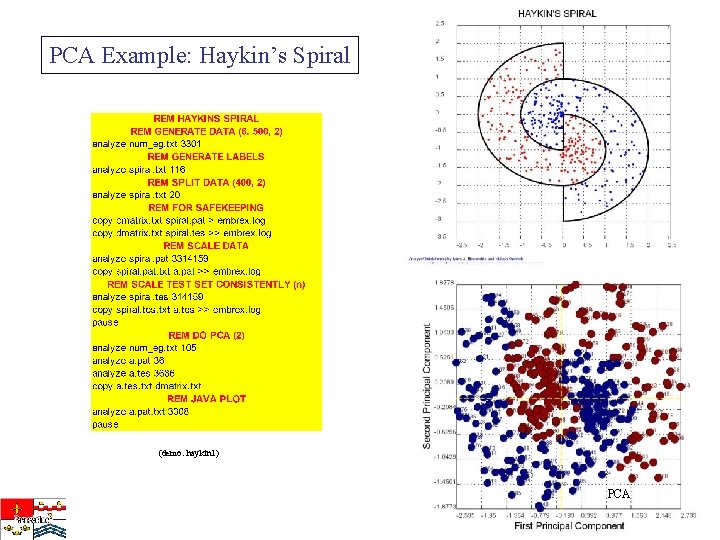
PCA Example: Haykin’s Spiral (demo: haykin 1) PCA
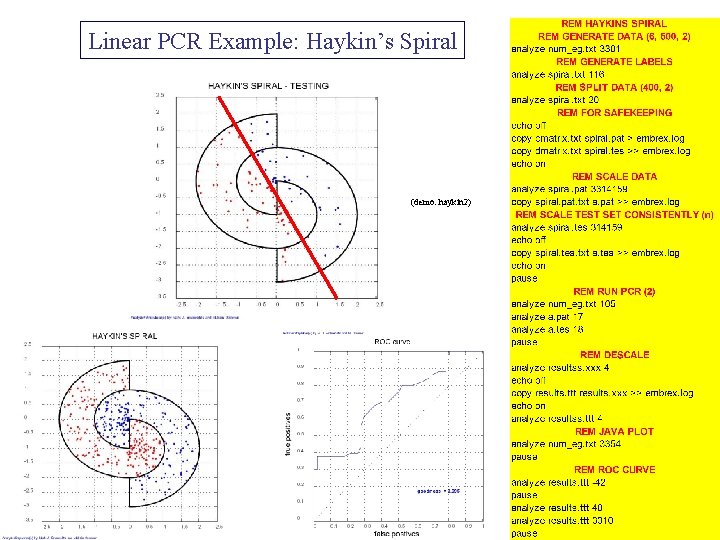
Linear PCR Example: Haykin’s Spiral (demo: haykin 2)
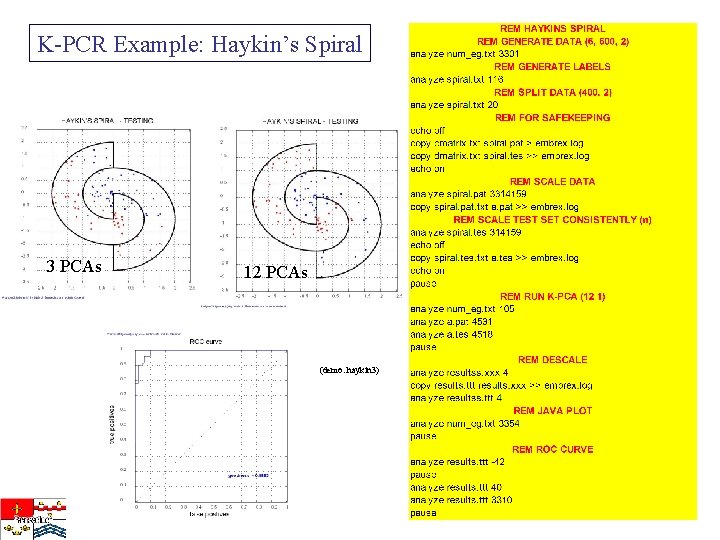
K-PCR Example: Haykin’s Spiral 3 PCAs 12 PCAs (demo: haykin 3)
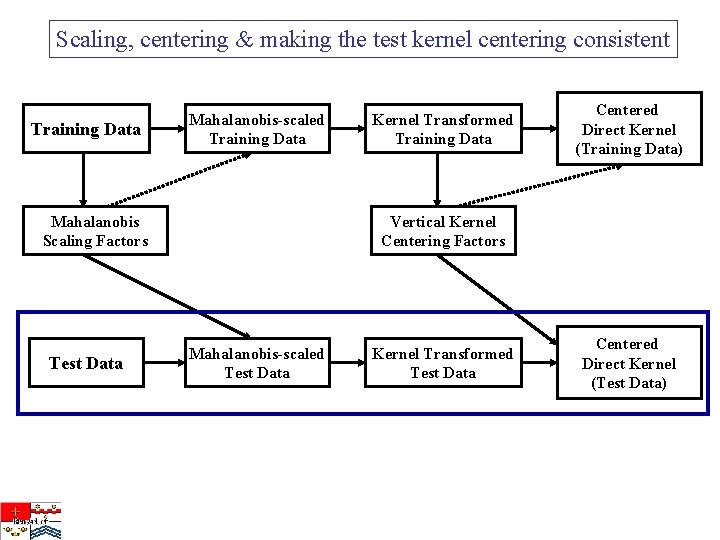
Scaling, centering & making the test kernel centering consistent Training Data Mahalanobis-scaled Training Data Mahalanobis Scaling Factors Test Data Kernel Transformed Training Data Centered Direct Kernel (Training Data) Vertical Kernel Centering Factors Mahalanobis-scaled Test Data Kernel Transformed Test Data Centered Direct Kernel (Test Data)
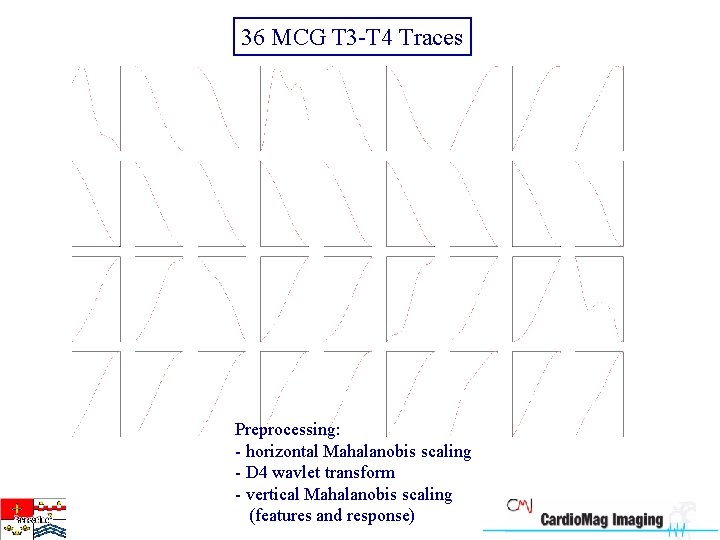
36 MCG T 3 -T 4 Traces Preprocessing: - horizontal Mahalanobis scaling - D 4 wavlet transform - vertical Mahalanobis scaling (features and response)
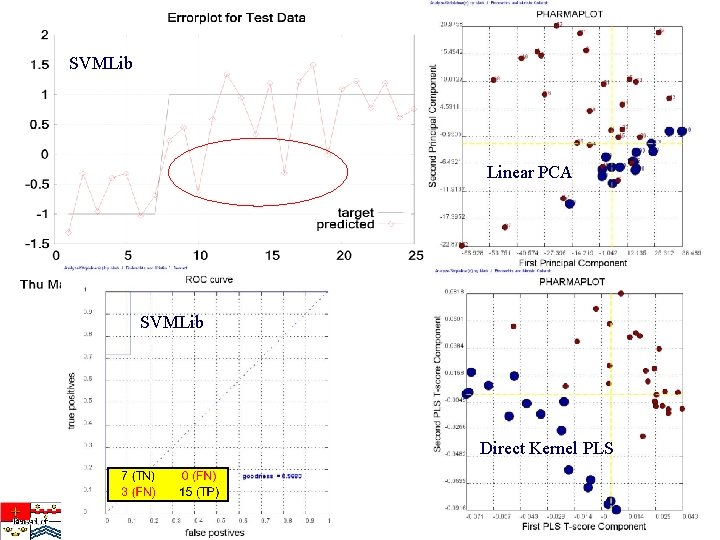
SVMLib Linear PCA SVMLib Direct Kernel PLS
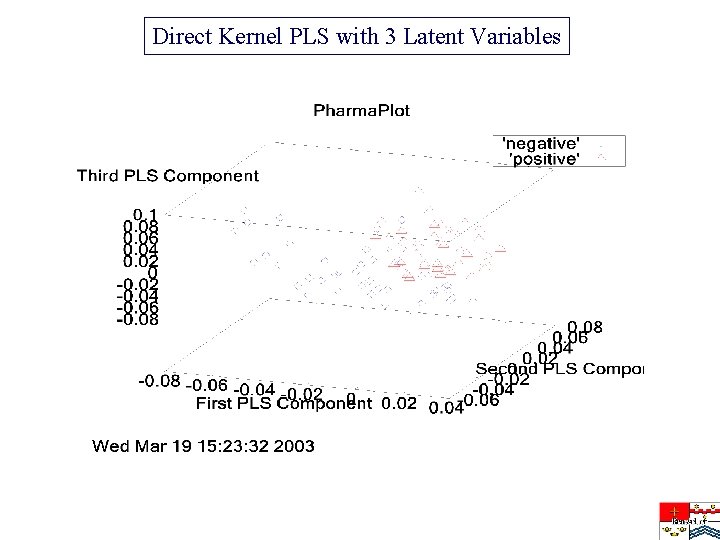
Direct Kernel PLS with 3 Latent Variables
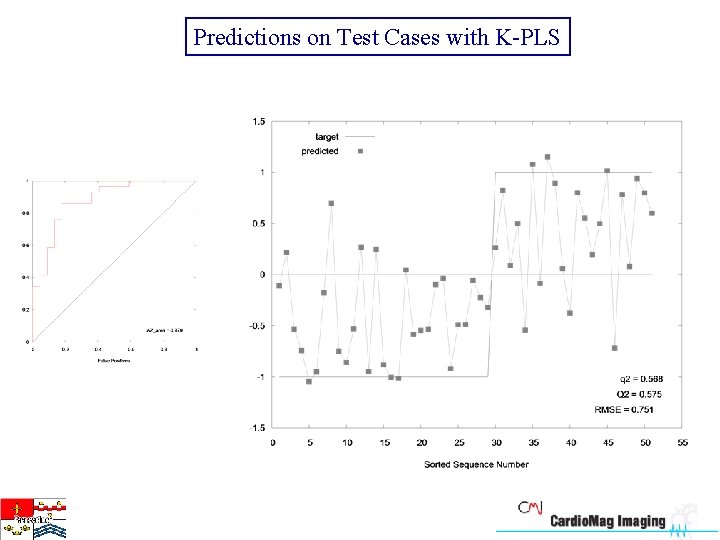
Predictions on Test Cases with K-PLS
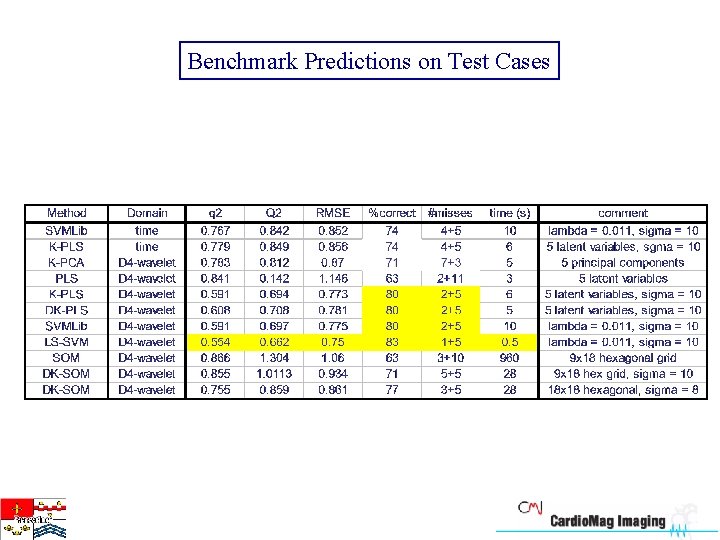
Benchmark Predictions on Test Cases
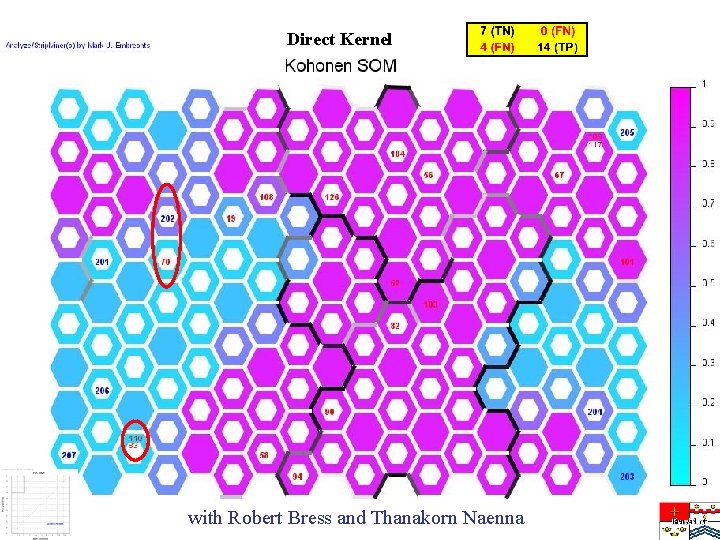
Direct Kernel with Robert Bress and Thanakorn Naenna
- Slides: 23