Presentation on Digital Door Lock Digital System Design

Presentation on Digital Door Lock Digital System Design Presenter: Subash Chandra Pakhrin 072 MSI 616 MSC in Information and Comm. Engineering Pulchowk Campus

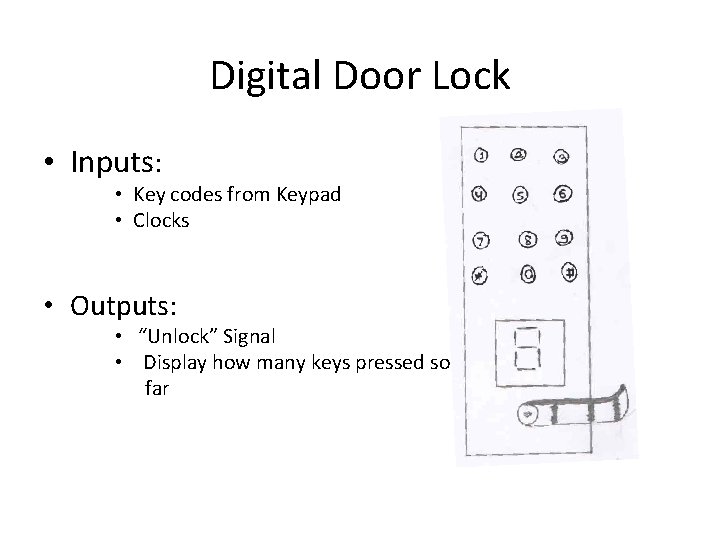
Digital Door Lock • Inputs: • Key codes from Keypad • Clocks • Outputs: • “Unlock” Signal • Display how many keys pressed so far

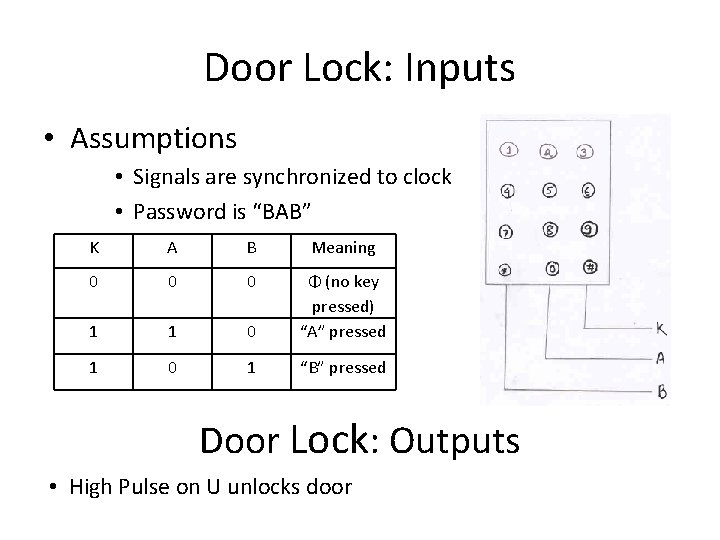
Door Lock: Inputs • Assumptions • Signals are synchronized to clock • Password is “BAB” K A B Meaning 0 0 0 1 1 0 Φ (no key pressed) “A” pressed 1 0 1 “B” pressed Door Lock: Outputs • High Pulse on U unlocks door

Strategy: 1. 2. 3. 4. 5. 6. 7. 8. Draw a state diagram (Moore Machine). Write O/P and next-state table. Encode states, inputs and outputs as bits. Choose a Flip Flop type. Construct an excitation table. Derive excitation equations from the table. Draw a output equations from the table. Draw a logic Diagram.

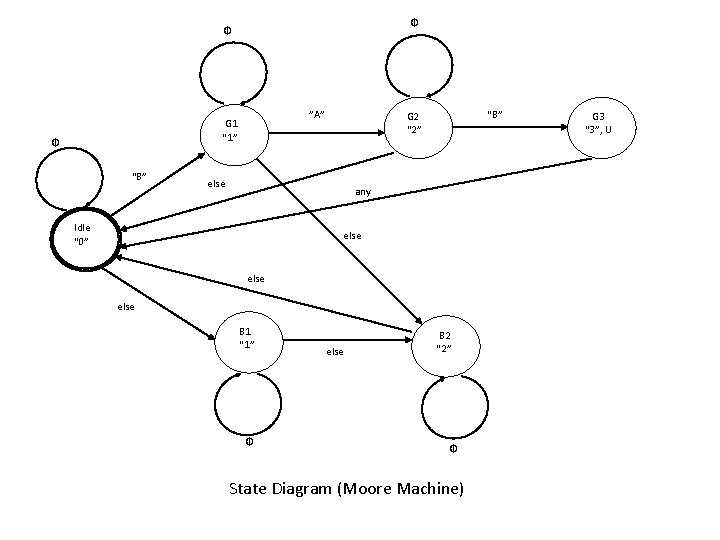
Φ Φ ”A” G 1 “ 1” Φ “B” G 2 “ 2” else any Idle “ 0” else B 1 “ 1” Φ else B 2 “ 2” Φ State Diagram (Moore Machine) G 3 “ 3”, U

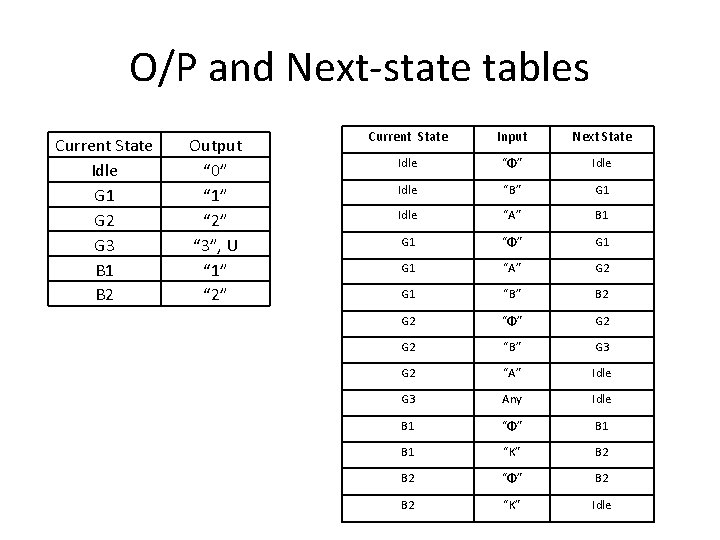
O/P and Next-state tables Current State Idle G 1 G 2 G 3 B 1 B 2 Output “ 0” “ 1” “ 2” “ 3”, U “ 1” “ 2” Current State Input Next State Idle “Φ” Idle “B” G 1 Idle “A” B 1 G 1 “Φ” G 1 “A” G 2 G 1 “B” B 2 G 2 “Φ” G 2 “B” G 3 G 2 “A” Idle G 3 Any Idle B 1 “Φ” B 1 “K” B 2 “Φ” B 2 “K” Idle

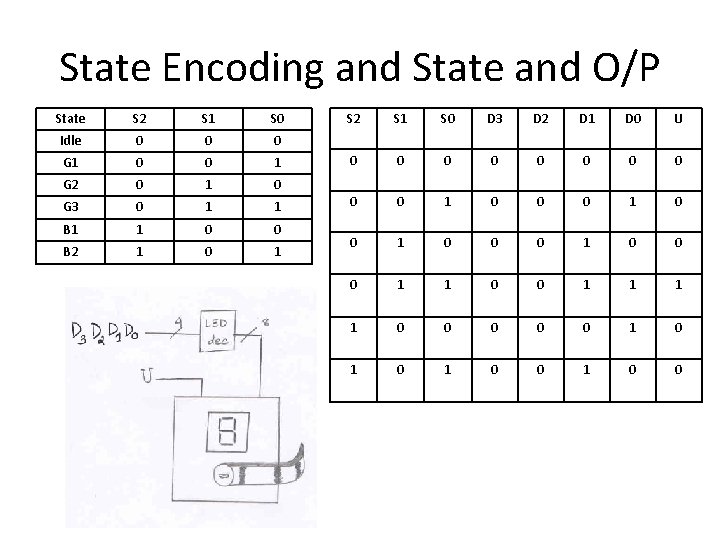
State Encoding and State and O/P State S 2 S 1 S 0 Idle 0 0 0 G 1 0 0 1 G 2 0 1 0 G 3 0 1 1 B 1 1 0 0 B 2 1 0 1 S 2 S 1 S 0 D 3 D 2 D 1 D 0 U 0 0 0 0 0 1 0 0 0 1 1 0 0 0 1 0 1 0 0

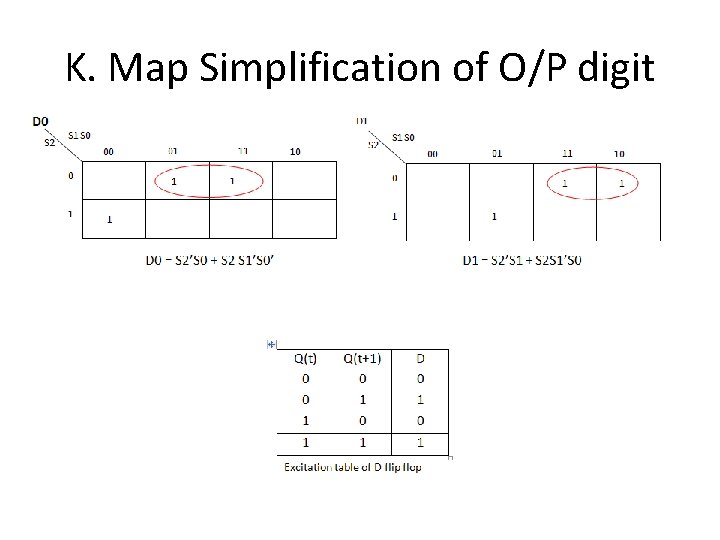
K. Map Simplification of O/P digit

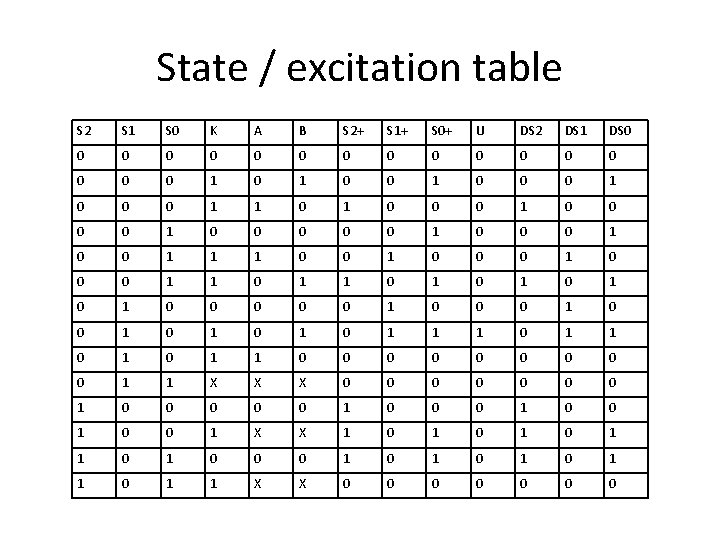
State / excitation table S 2 S 1 S 0 K A B S 2+ S 1+ S 0+ U DS 2 DS 1 DS 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 1 1 1 0 0 0 1 1 0 1 0 1 0 0 1 0 1 0 1 1 0 0 0 0 0 1 1 X X X 0 0 0 0 1 0 0 1 X X 1 0 1 0 1 0 0 0 1 0 1 1 X X 0 0 0 0

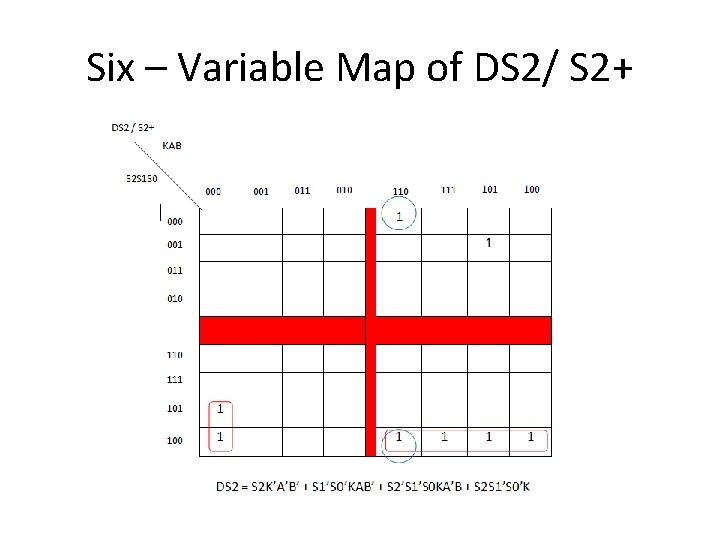
Six – Variable Map of DS 2/ S 2+

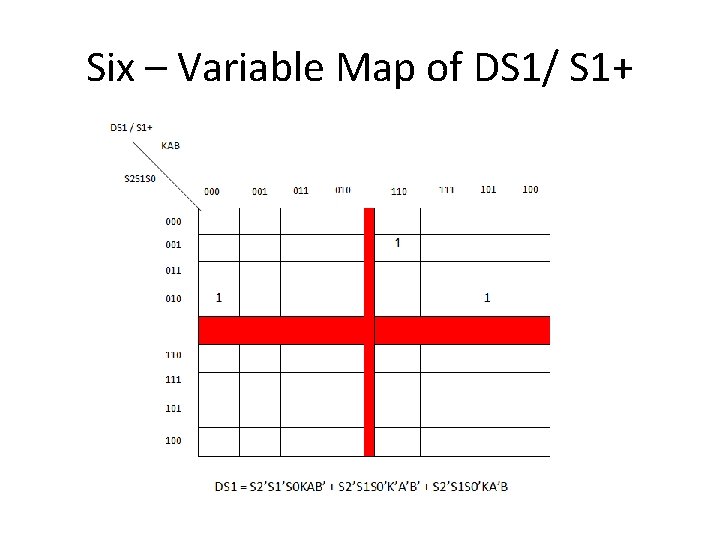
Six – Variable Map of DS 1/ S 1+

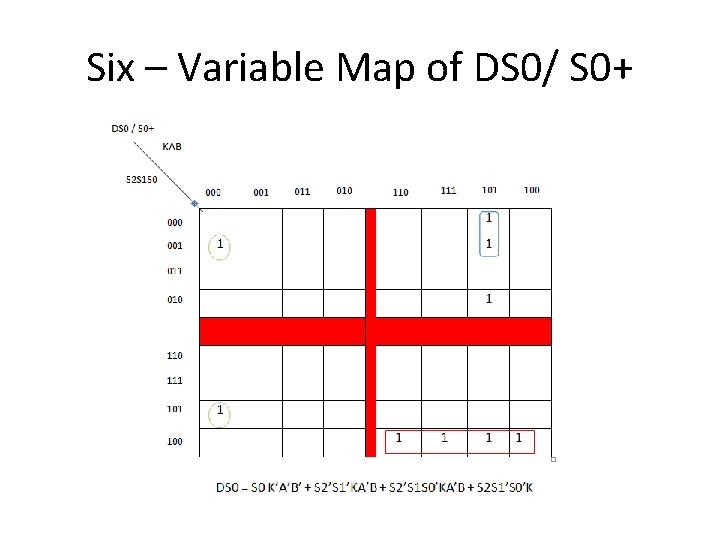
Six – Variable Map of DS 0/ S 0+

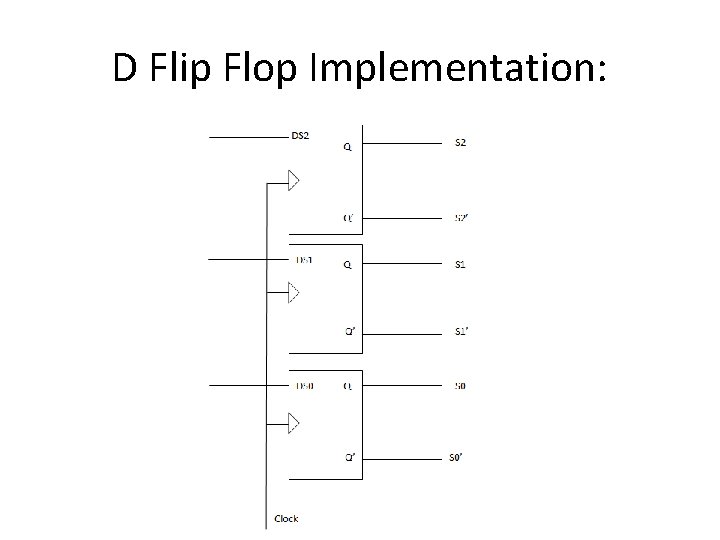
D Flip Flop Implementation:

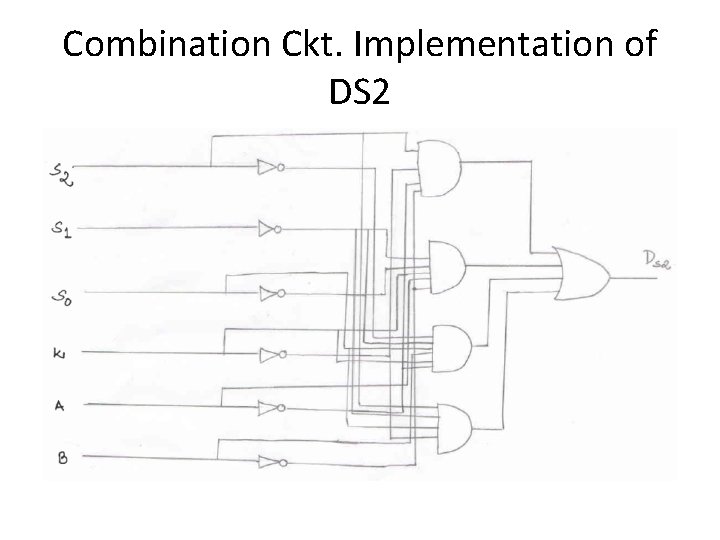
Combination Ckt. Implementation of DS 2

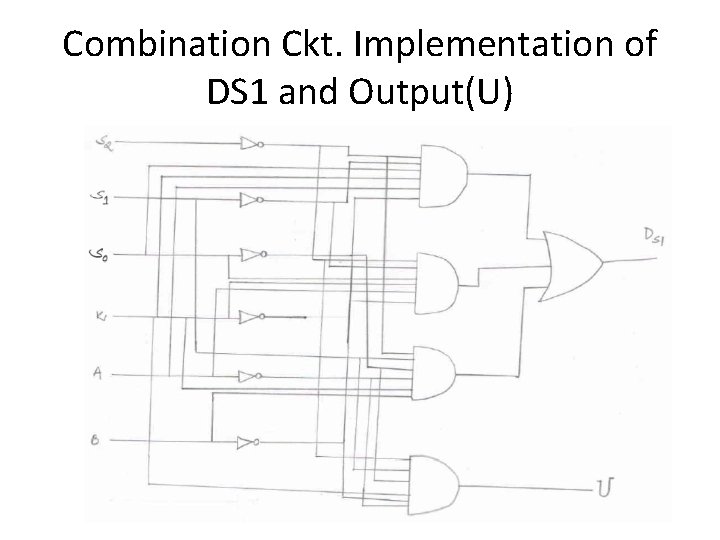
Combination Ckt. Implementation of DS 1 and Output(U)

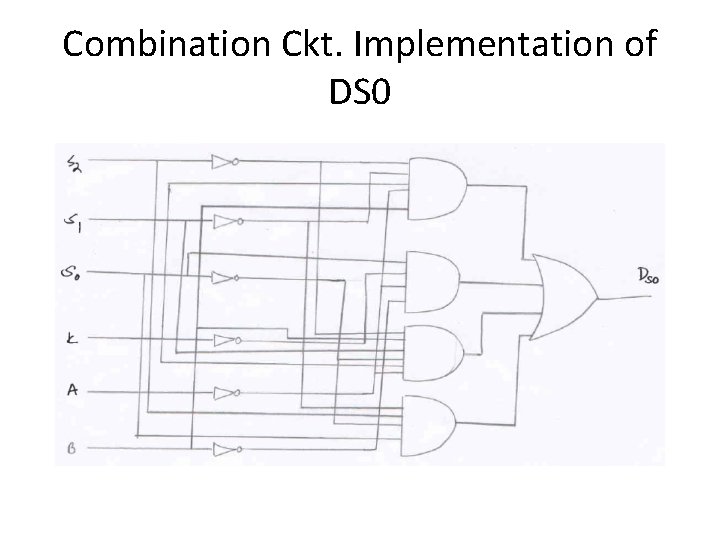
Combination Ckt. Implementation of DS 0

Thank You.