Presentation 3 More about the Sampling Distribution of

Presentation 3 More about the Sampling Distribution of the Sample Mean and introduction to the t-distribution 1

Brief Review of Sampling Distributions Sampling Distribution of Sample Proportion: n Each member of the population has a trait of interest with probability p (population proportion). n Suppose a random sample of size n is obtained form the population. n The sample proportion p-hat is a logical estimator of p, n If the sample is large enough, np and n(1 -p) >5, then 2

Sampling Distribution of Sample Mean n Let X be a random variable and the statistic be the sample mean of X in a random sample of size n. We examine the sampling distribution of in the following three scenarios: 1. When X is a normal random variable, E(X)=µ and s. d. (X)= σ are both known. 2. When X is not a normal random variable, E(X)=µ and s. d. (X)= σ are both known and the sample size is large, n ≥ 30. 3. When X is a normal random variable, E(X)=µ is known, s. d. (X)= σ is unknown and the sample size is large, n ≥ 30. So far we have seen the first two cases. 3

n Case 1: n Case 2: n Case 3: , where tn-1 denotes the t-distribution with n -1 degrees of freedom. 4

Properties of the t-distribution n n n There are infinitely many t-distributions, each characterized by one parameter, the degrees of freedom. The degrees of freedom are positive integers, e. g. t 1, t 2 , t 3, …, t 10, … Random variables with t-distribution are continuous. The density curve of a t - distribution is symmetric, bell-shaped and centered at zero (similar to the standard normal curve). There are tables for the probabilities related with a t – random variable. In will see how to use them later in the course. As the degrees of freedom increase, the variance of the t -random variable decreases, i. e. the density curve is less spread, and actually it approaches the standard normal density. 5

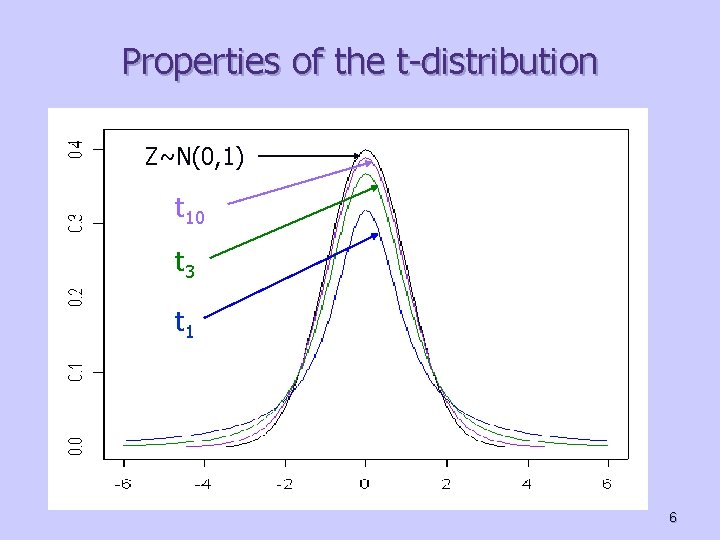
Properties of the t-distribution Z~N(0, 1) t 10 t 3 t 1 6