Presentation 2 Basic Concepts of Probability OBJECTIVES Use

Presentation 2 : Basic Concepts of Probability

OBJECTIVES ØUse the Fundamental Counting Principle ØDistinguish among classical probability, empirical probability, and subjective probability ØDetermine the probability of the complement of an event ØUse a tree diagram and the Fundamental Counting Principle to find probabilities

FUNDAMENTAL COUNTING PRINCIPLE Fundamental Counting Principle ØIf one event can occur in m ways and a second event can occur in n ways, the number of ways the two events can occur in sequence is m*n. ØCan be extended for any number of events occurring in sequence.

Example: Fundamental Counting Principle You are purchasing a new car. The possible manufacturers, car sizes, and colors are listed. Manufacturer: Ford, GM, Honda Car size: compact, midsize Color: white (W), red (R), black (B), green (G) How many different ways can you select one manufacturer, one car size, and one color? Use a tree diagram to check your result.

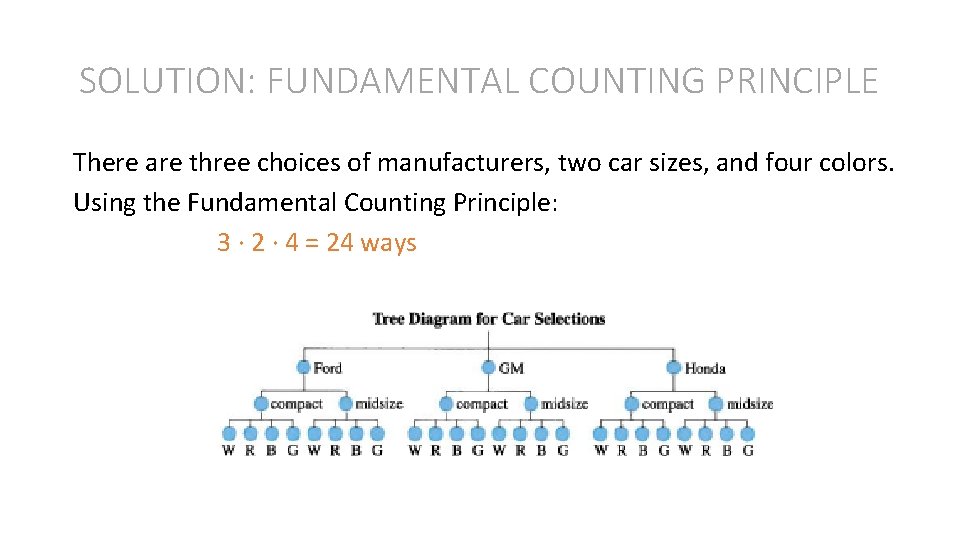
SOLUTION: FUNDAMENTAL COUNTING PRINCIPLE There are three choices of manufacturers, two car sizes, and four colors. Using the Fundamental Counting Principle: 3 ∙ 2 ∙ 4 = 24 ways

FUNDAMENTAL COUNTING PRINCIPLE PRACTICE ØA breakfast restaurant offers a $7. 50 special. You get your choice of how your eggs are cooked (fried, scrambled, poached), breakfast meat (bacon or sausage), bread (toast, biscuit, English muffin), and drink (juice or coffee). How many options for breakfast are there? ØA realtor uses a lock box to store keys in homes for sale. The lock box code is 4 digits; the first number cannot be 0 and the last number cannot be even. How many different codes are there?

NOTATION ØP denotes probability ØCapital letters (A, B, C) denote events ØP(A) denotes the probability that event A occurs

RANGE OF PROBABILITIES RULE Range of probabilities rule ØThe probability of an event E is between 0 and 1, inclusive. Ø 0 ≤ P(E) ≤ 1 Impossible [ 0 Unlikely Even chance 0. 5 Likely Certain ] 1

TYPES OF PROBABILITY Classical (theoretical) Probability ØEach outcome in a sample space is equally likely. Ø

EXAMPLE: FINDING CLASSICAL PROBABILITIES ØYou roll a six-sided die. Find the probability of each event. 1. Event A: rolling a 3 2. Event B: rolling a 7 3. Event C: rolling a number less than 5

EXAMPLE: FINDING CLASSICAL PROBABILITIES ØYou roll a six-sided die. Find the probability of each event. 1. Event A: rolling a 3 2. Event B: rolling a 7 3. Event C: rolling a number less than 5 Solution: Sample space: {1, 2, 3, 4, 5, 6}

SOLUTION: FINDING CLASSICAL PROBABILITIES 1. Event A: rolling a 3 2. Event B: rolling a 7 Event A = {3} Event B= { } (7 is not in the sample space) 3. Event C: rolling a number less than 5 Event C = {1, 2, 3, 4}

CLASSICAL PROBABILITIES ØA probability experiment consists of rolling a 16 sided die. Find the probability of the event. ØRolling an 8. ØRolling a number greater than 9. ØRolling a number divisible by 4.