Presentation 1 1 2 Event Operations and Properties

Presentation 1 -1 -2: Event Operations and Properties Ga. Probability and Statistics: r retfort Beginners and A Primer Ord Pre-Beginners ner Prologue to the Prologue: Set Theory Part Two: Event Operations and Properties Primary reference: Casella-Berger 2 nd Edition

Presentation 1 -1 -2: Event Operations and Properties There’s other stuff we can do with events. We can combine them, in a union: Gar rett Ord ner (union) We can keep only the outcomes they have in common, in their intersection: (intersection ) 2

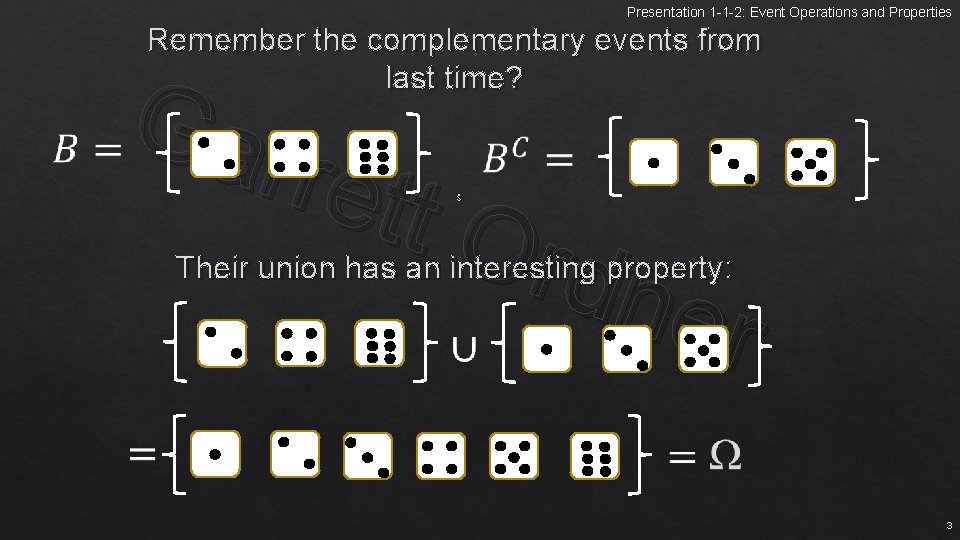
Presentation 1 -1 -2: Event Operations and Properties Remember the complementary events from last time? Gar rett Ord ner , Their union has an interesting property: 3

Presentation 1 -1 -2: Event Operations and Properties Their intersection has a far less-interesting property: Gar rett Ord ner (empty set) Remember we called those events B and BC? Well, now it doesn’t matter what’s in them; we can generalize! For any event B and its complement BC : 4

Presentation 1 -1 -2: Event Operations and Properties Gar r e tt O ! rdn er Caution! We’re about to enter Venn Diagram territory. Casella, Berger, and my old stats theory professor would (presumably) all like me to remind you that diagrams can illustrate, but they don’t prove anything (and we aren’t going to write out many proofs in this course, so go buy the book). Whatever you do, don’t draw them on your exams!!! 5

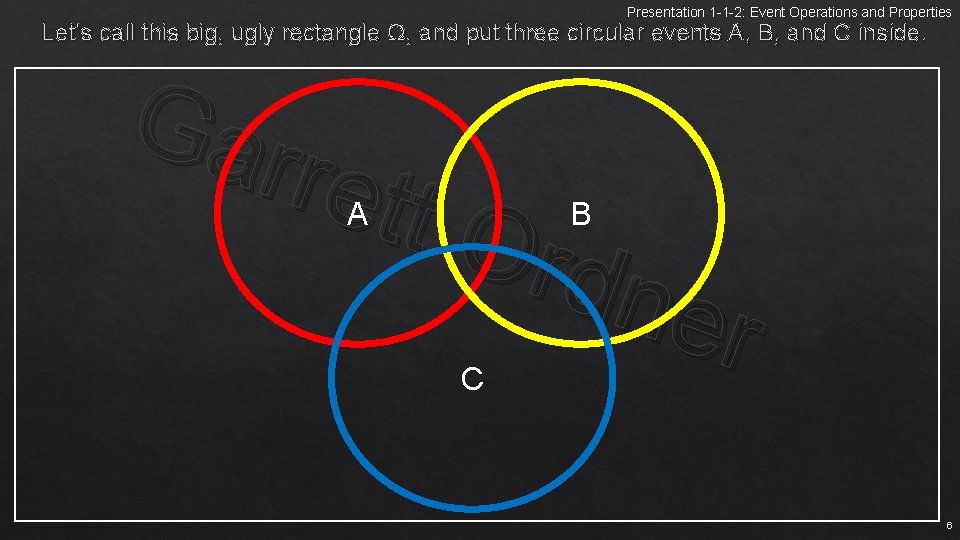
Presentation 1 -1 -2: Event Operations and Properties Let’s call this big, ugly rectangle Ω, and put three circular events A, B, and C inside. Gar rett Ord ner B A C 6

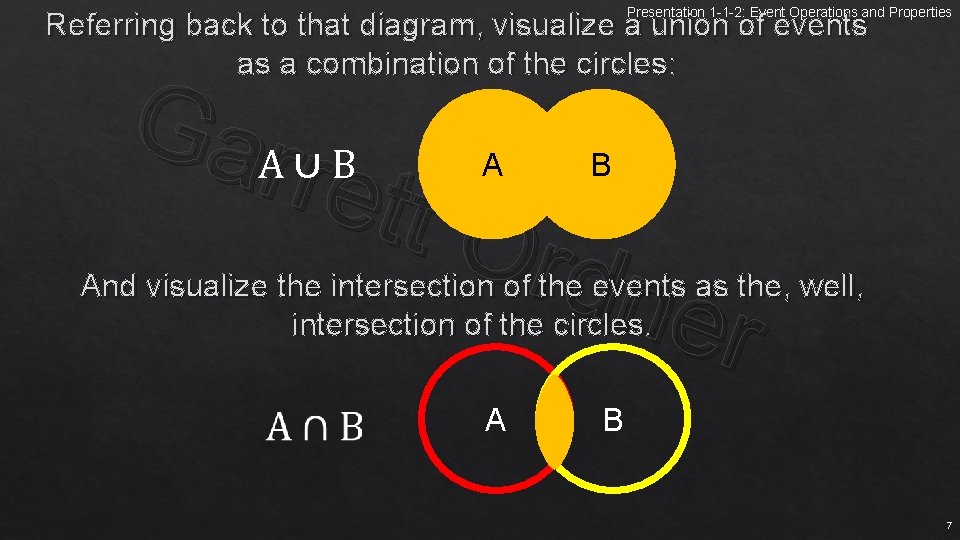
Presentation 1 -1 -2: Event Operations and Properties Referring back to that diagram, visualize a union of events as a combination of the circles: Gar. A ∪ B rett Ord ner A B And visualize the intersection of the events as the, well, intersection of the circles. A B 7

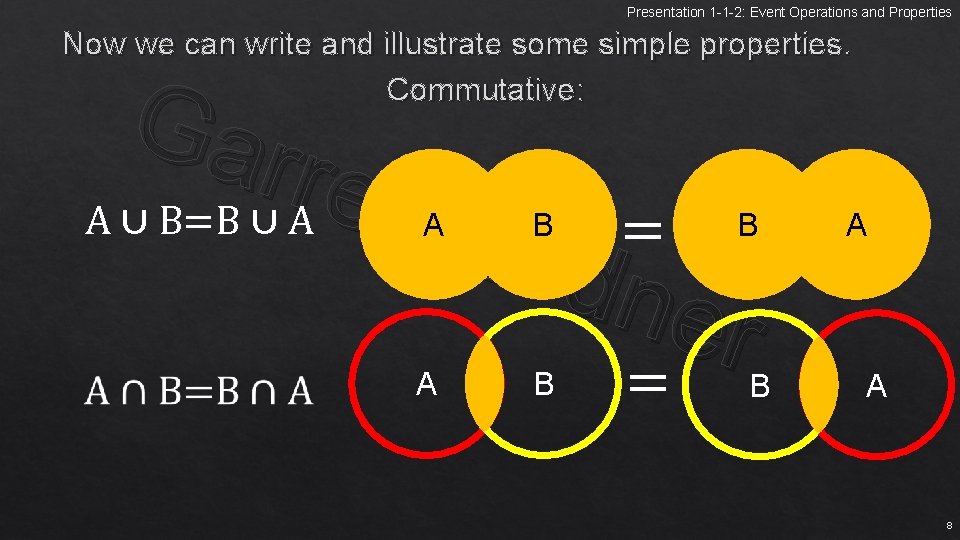
Presentation 1 -1 -2: Event Operations and Properties Now we can write and illustrate some simple properties. Commutative: Gar r e A ∪ B=B ∪ A tt = Ord ner = A B B B A A 8

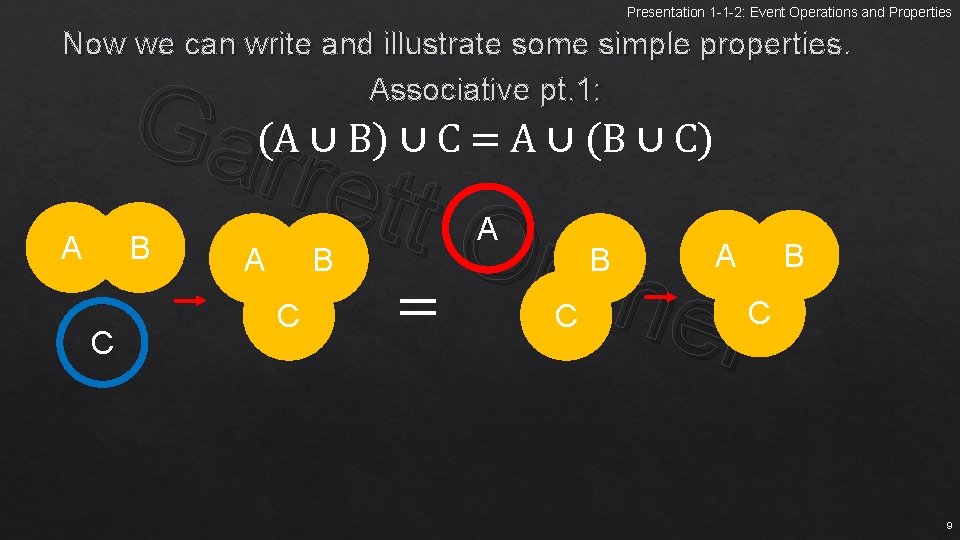
Presentation 1 -1 -2: Event Operations and Properties Now we can write and illustrate some simple properties. Associative pt. 1: A Gar(A ∪ B) ∪ C = A ∪ (B ∪ C) rett Ord ner = B C A B C 9

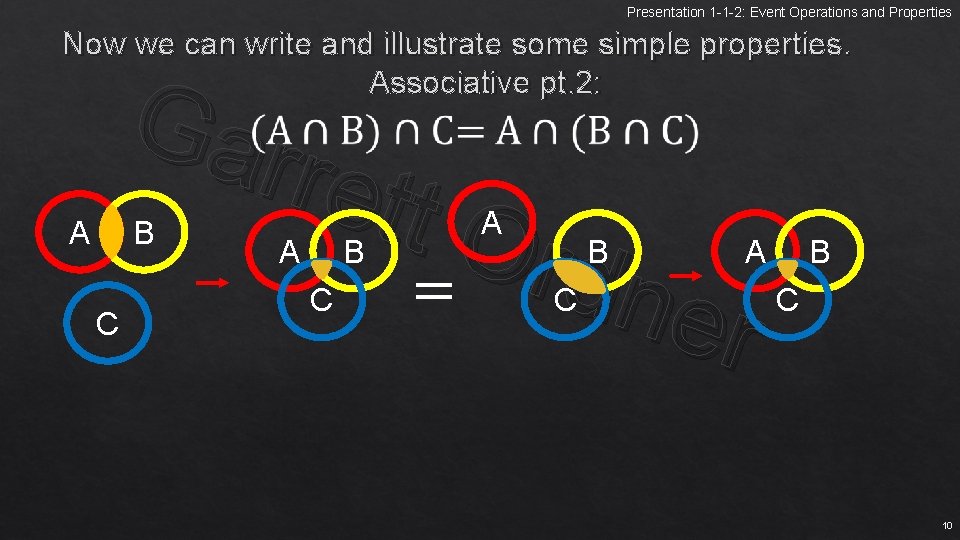
Presentation 1 -1 -2: Event Operations and Properties Now we can write and illustrate some simple properties. Associative pt. 2: Gar rett O r dne = r B A C A B C B A C 10

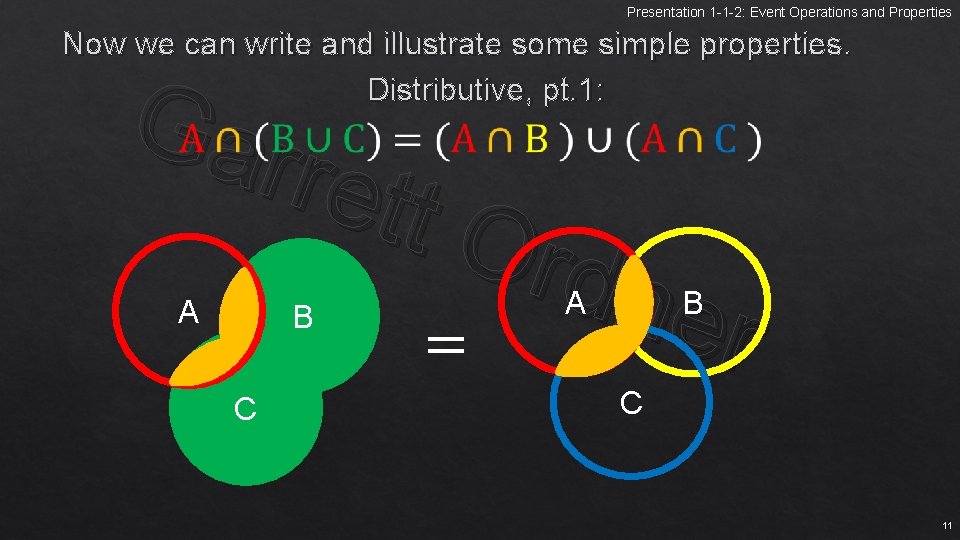
Presentation 1 -1 -2: Event Operations and Properties Now we can write and illustrate some simple properties. Distributive, pt. 1: Gar rett Ord n e = r A B C B A C 11

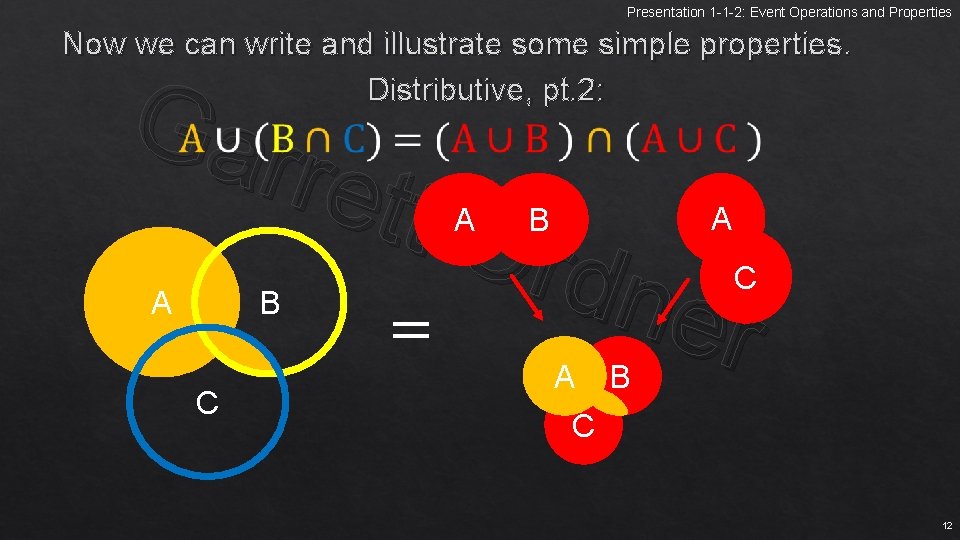
Presentation 1 -1 -2: Event Operations and Properties Now we can write and illustrate some simple properties. Distributive, pt. 2: Gar rett Ord n er = A A A B C 12

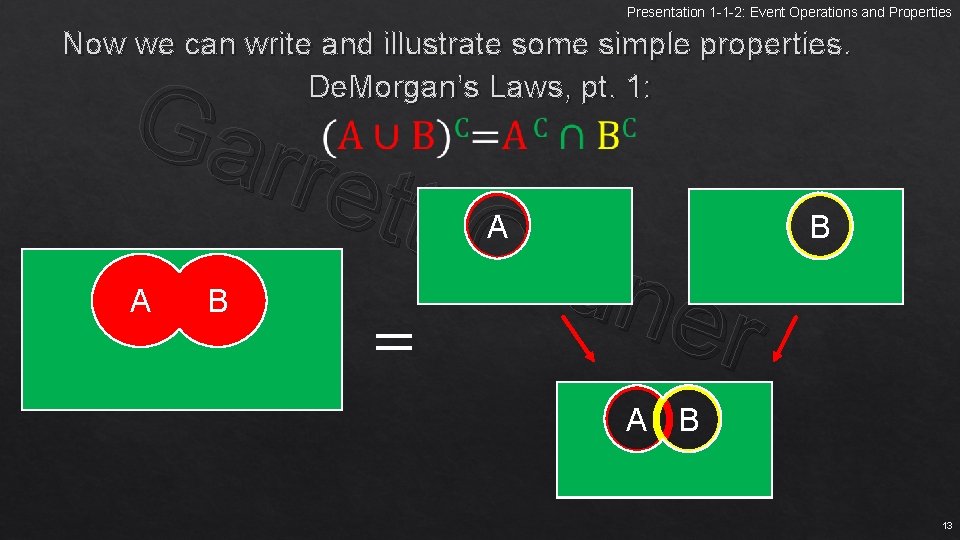
Presentation 1 -1 -2: Event Operations and Properties Now we can write and illustrate some simple properties. De. Morgan’s Laws, pt. 1: Gar rett Ord n e = r A A B B A B 13

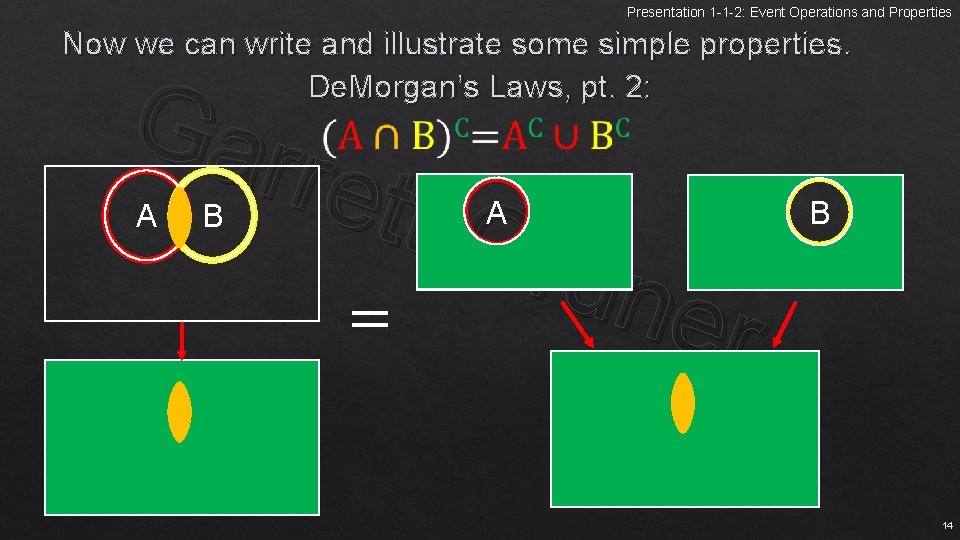
Presentation 1 -1 -2: Event Operations and Properties Now we can write and illustrate some simple properties. De. Morgan’s Laws, pt. 2: Gar rett Ord ner = A B 14