Prerequisites Almost essential Welfare Basics Frank Cowell Microeconomics

Prerequisites Almost essential Welfare Basics Frank Cowell: Microeconomics October 2006 Design Basics MICROECONOMICS Principles and Analysis Frank Cowell

Overview. . . Design Basics Frank Cowell: Microeconomics A parable AN introduction to the issues Social choice again Mechanisms The design problem

A parable Frank Cowell: Microeconomics n Think through the following everyday situation u u u n What is the decision problem? u u u n Alf, Bill and Charlie have appointments at the same place but different times they try to book taxis, but there’s only one available so they’ll have to share! do they care about being early/late? do they care about the others’ objectives? clearly a joint problem with conflicting interests Consider a proposed solution u u u if taxi firm suggests an efficient pickup time – accept otherwise ask for the earliest preferred time by A, B, C look at this in a diagram…

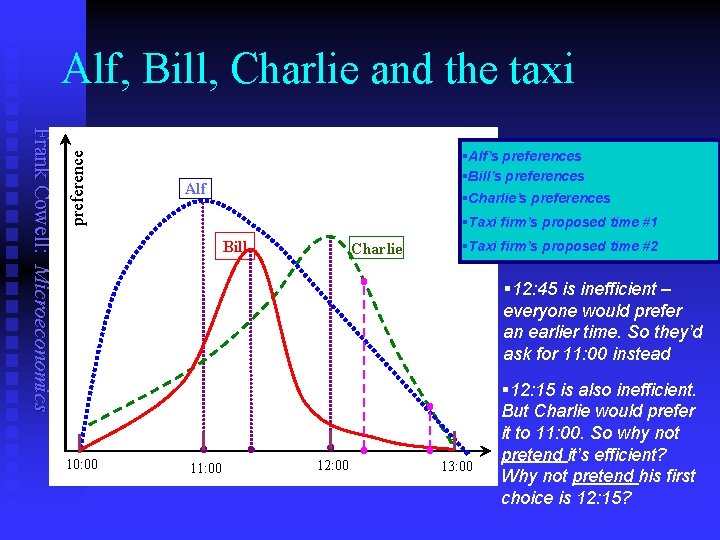
Frank Cowell: Microeconomics preference Alf, Bill, Charlie and the taxi §Alf’s preferences §Bill’s preferences Alf §Charlie’s preferences §Taxi firm’s proposed time #1 Bill Charlie §Taxi firm’s proposed time #2 § 12: 45 is inefficient – everyone would prefer an earlier time. So they’d ask for 11: 00 instead 10: 00 11: 00 12: 00 13: 00 § 12: 15 is also inefficient. But Charlie would prefer it to 11: 00. So why not pretend it’s efficient? Why not pretend his first choice is 12: 15?

The approach Frank Cowell: Microeconomics n Some questions: u u u n Manipulation (sometimes “cheating” or “chiselling”): u u n an important connection with the issue of efficiency rules might be inefficient because they provide wrong incentives Design problem: u u u n what properties should a taxi rule satisfy? would Alf, Bill or Charlie want to misrepresent preferences? could we find a problem of manipulation? find a rule so that individuals choose a socially desirable outcome but will only do so if it is in their private interests what is “socially desirable”…? Need to examine the representation of choices u u build on the analysis from social welfare… …and reuse some results

Overview. . . Design Basics Frank Cowell: Microeconomics A parable A link with the fundamentals of welfare economics Social choice again Mechanisms The design problem

Agenda Frank Cowell: Microeconomics n Basic questions u u u n Purpose u u n modelling group objectives… …need a review of social choice Information u u n purpose of design informational context strategic setting agents may have private information… …so need to allow for the possibility of misrepresentation Strategy u u a connection with game-theoretic approaches… …so need to review concepts of equilibrium Begin with purpose

Social states and preferences Frank Cowell: Microeconomics n Social state: q u u n n Set of all social states: Q Preferences vh(∙) u u n a comprehensive description… …of all relevant features of the economy in question a “reduced form” version of agent h’s utility function utility of agent h given social state q is vh(q) preference profile is an ordered list, one for each agent: [v 1, v 2, v 3, …] a list of functions, not utility levels Set of all preference profiles: V

A reminder Frank Cowell: Microeconomics n Constitution u u u n Properties u u n Universality Pareto Unanimity Independence of Irrelevant Alternatives Non-Dictatorship Arrow theorem u u n a mapping from V to set of all v(∙) given a particular set of preferences for the population… …the constitution should determine a specific v(∙) if there are more than two social states then there is no constitution satisfying the above four properties a key result Use this reminder to introduce a new concept…

Social-choice function Frank Cowell: Microeconomics n A social choice function G u u u n Note that argument of the SCF is same as for constitution u u n a mapping V Q given a particular set of preferences for the population… …picks out exactly one chosen element from Q a profile of preferences [v]… … a list of utility functions But that it produces a different type of “animal” u u the constitution uses [v] to yield a social ordering the SCF uses [v] to yield a social state

Social-choice function: properties Frank Cowell: Microeconomics n Three key properties of an SCF, G : n G is Paretian if… u u n G is monotonic if… u u n given a q* such that vh(q*) ≥ vh(q), for all h and all q Q, then q* = G(v 1, v 2, v 3, …) [ ] and [v [ ] V such that given any [v “vh(q*)≥vh(q)” implies “vh(q*)≥vh(q)” “ * = G(v 1, v 2, v 3, …)” implies “q “ * = G(v 1, v 2, v 3, …)” then “q G is dictatorial if u there is some agent whose preferences completely determine q

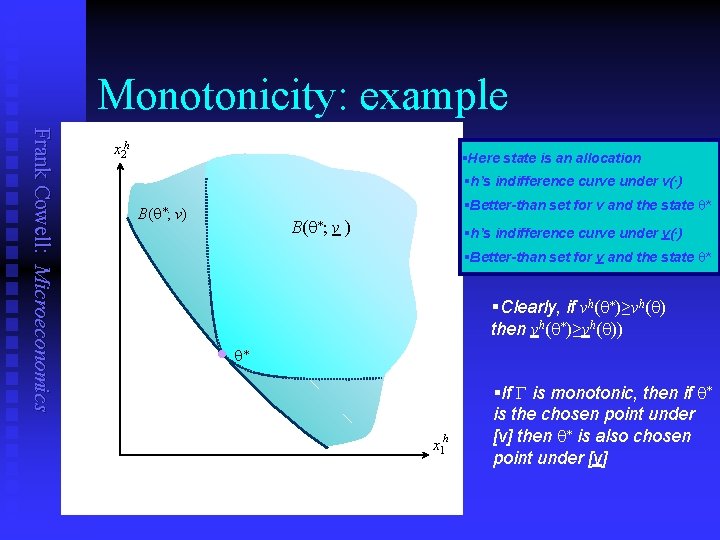
Monotonicity: example Frank Cowell: Microeconomics x 2 h §Here state is an allocation §h’s indifference curve under v(∙) §Better-than set for v and the state q* B(q*; v) B(q*; v ) §h’s indifference curve under v(∙) §Better-than set for v and the state q* §Clearly, if vh(q*)≥vh(q) then vh(q*)≥vh(q)) · q* x 1 h §If G is monotonic, then if q* is the chosen point under [v] then q* is also chosen point under [v]

Social-choice function: result Frank Cowell: Microeconomics n Suppose Q has more than two elements… … and that G is defined for all members of V. Then, if G is Paretian and monotonic… … G must also be dictatorial n A counterpart of the Arrow result on constitutions n n n

A key property of the SCF Frank Cowell: Microeconomics n G is manipulable if there is a profile [v] V such that… u u n Significance is profound: u u u n …for some h and some other utility function vh(∙) v h (q ) > v h (q ) where q = G(v 1, …, vh, …, ) and q = G(v 1, …, vh, …, ) if G is manipulable then some agent h should realise… …that if h misrepresents his preferences but others tell the truth …then h will be better off An incentive to misrepresent information? u u does imply that there is some h who can manipulate… …but it does mean that, under some circumstances there is an h who could manipulate

Social-choice function: another result Frank Cowell: Microeconomics n Note that the monotonicity property is powerful: u u n From this and the previous result a further result follows u u u n if G is monotonic … …then G cannot be manipulable suppose Q has more than two elements… for each h any strict ranking of elements of Q is permissible then a Paretian, non-manipulable SCF G must be dictatorial This result is important u u connects the idea of misrepresentation and social choice introduces an important part of the design problem

Social-choice function: summary Frank Cowell: Microeconomics n Similar to the concept of constitution u n Not surprising to find result similar to Arrow u u n but from the set of preference profiles to the set of social states introduce weak conditions on the Social-choice function there’s no SCF that satisfies all of them But key point concerns link with information u u misrepresentation and manipulability are linked important implication for design problem

Overview. . . Design Basics Frank Cowell: Microeconomics A parable The problem of implementation… Social choice again Mechanisms The design problem

Forward from social choice Frank Cowell: Microeconomics n Social choice is just the first step u u n The next step involves achievement u u u n SCF describes what is desirable… …not how you achieve it reconcile desirable outcomes with individual incentives the implementation problem underlies practical policy making Requires the introduction of a new concept u a mechanism

Implementation Frank Cowell: Microeconomics n Is the SCF consistent with private economic behaviour? u u n Implementation problem: find an appropriate mechanism u u n mechanism is a partially specified game of imperfect information… rules of game are fixed strategy sets are specified preferences for the game are not yet specified Plug preferences into the mechanism: u u u n Yes if the q picked out by G is also… … the equilibrium of an appropriate economic game Does the mechanism have an equilibrium? Does the equilibrium correspond to the desired social state q? If so, the social state is implementable There are many possible mechanisms

Mechanism: example Frank Cowell: Microeconomics n n The market is an example of a mechanism Suppose the following things are given: u u u n Mechanism consists of institutions and processes determining u u u n resource ownership in the economy other legal entitlements production technology incomes… production allocations … consumption baskets Once individuals’ preferences are specified u u market maps preferences into prices… …price system yields a specific state of the economy q

Design: basic ingredients Frank Cowell: Microeconomics n The agents’ strategy sets S 1, S 2, S 3, …. u u n The outcome function g u u n collectively write S : = S 1£S 2£S 3£… each element of S is a profile [s 1, s 2, s 3, …] given a strategy profile s : = [s 1, s 2, s 3, …] … … social state is determined as q = g (s) Agents’ objectives u u u a profile of preferences [v] : = [v 1, v 2, v 3, …] once the outcome q is determined… …get utility payoffs v 1(q ), v 2(q ), v 3(q ), ….

Mechanism Frank Cowell: Microeconomics n n Consider this more formally A mechanism consists of u u n n The mechanism is an almost-completely specified game. All that is missing is the collection of utility functions u u n the set of strategy profiles S and an outcome function g from S to the set of social states Q. these specify the objective of each agent h and the actual payoff to each h Once a particular profile of utility functions is plugged in: u u we know the social state that will be determined by the game… … and the welfare implications for all the economic agents

Implementation: detail Frank Cowell: Microeconomics n n n Is the SCF consistent with private economic behaviour? Mechanism is a (strategy-set, outcome-function) pair (S; g). Agents’ behaviour: u u u n The outcome function u u n given their preferences [v 1, v 2, v 3, …] use the mechanism as the rules of the game determine optimal strategies as the profile [s*1, s*2, s*3, …] determines social from the profile of strategies q* = g(s*1, s*2, s*3, …) Is this q* the one that the designer would have wished from the social-choice function G? a formal statement

Dominant-strategy implementation Frank Cowell: Microeconomics n Consider a special interpretation of equilibrium… n Take a particular social-choice function G Suppose there is a dominant-strategy equilibrium of the mechanism (S; g (∙)): n [s*1(∙), s*2(∙), s*3(∙), …] n If it is true that u n g(s*1(v 1), s*2(v 2), s*3(v 3), …) = G(v 1, v 2, v 3, …) Then mechanism (S; g (∙)) weakly implements the G in dominant strategies

Direct mechanisms Frank Cowell: Microeconomics n For exposition consider a very simple mechanism u n Map from profile of preferences to states u u u n The direct mechanism Involves a very simple game. The game is “show me your utility function” Enables direct focus on the informational aspects of implementation For a direct mechanism u u u strategy sets are just sets of preferences S = V so the outcome function and the social-choice function are the same g(v 1 , v 2 , v 3 , …) = G(v 1 , v 2 , v 3 , …) the mechanism is effectively just the SCF

Truthful implementation Frank Cowell: Microeconomics n n An SCF that encourages misrepresentation is of limited use Is truthful implementation possible? u u n Will people announce their true attributes? Will it be a dominant strategy to do so? G is truthfully implementable in dominant strategies if s*h (vh ) = vh h = 1, 2, … is a dominant-strategy equilibrium of the direct mechanism n Specifying a dominant strategies is quite strong u u u we insist that everyone finds that “honesty is the best policy” irrespective of whether others are following the same rule irrespective of whether others are even rational another key result

Revelation principle Frank Cowell: Microeconomics n n Take a social-choice function G Suppose that mechanism (S; g) can weakly implement G u u u n Now consider a direct mechanism u n maps profiles from V to social states in Q. We can always get truthful implementation of G in dominant-strategies u u n for any [v] V… … (S; g) has at least one equilibrium [s*1(v 1), s*2(v 2), s*3(v 3), …]… …such that q* = g(s*1(v 1), s*2(v 2), s*3(v 3), …) = G(v 1, v 2, v 3, …) vh h = 1, 2, …is 1, 2, … a dominant-strategy equilibrium of the direct mechanism q* = G(v 1, v 2, v 3, …) Formally stated the result is: u If G is weakly implementable in dominant strategies by the mechanism (S; g) then G is truthfully implementable in dominant strategies using the direct mechanism (V; G)

The revelation principle Frank Cowell: Microeconomics §Pick a preference profile [v] from V §Agents select strategies §Outcome function yields social state S 2 *1 [s V ( • * ), s ( … • ), ] §The combined effect g ( • ) §Direct mechanism simply requires declaration of [v] Q G( • ) = g (s*1( • ), s*2( • ), …)

Direct mechanisms: manipulability Frank Cowell: Microeconomics n Reinterpret manipulability in terms of direct mechanisms: u u n How does the person “really” feel about q and q? u u n if all, including h, tell the truth about preferences: q = G(v 1, …, vh, …, ) if h misrepresents his preferences but others tell the truth: q = G(v 1, …, vh, …, ) if vh(q) > vh(q) there is an incentive to misrepresent information if h realises then clearly G is manipulable What type of SCF would be non-manipulable? u u need to characterise a class of G central issue of design

Overview. . . Design Basics Frank Cowell: Microeconomics A parable Allowing for human nature… Social choice again Mechanisms The design problem

The core of the problem Frank Cowell: Microeconomics n n Focus on a coherent approach to the implementation problem How to design a mechanism so that agents truthfully reveal private information They only do so if it is in their private interests to act this way Take a standard form of implementation u mechanism has equilibrium in dominant strategies another key result

Gibbard-Satterthwaite Frank Cowell: Microeconomics n n The G-S result can be stated in several ways A standard versions is: u u n n if the set of social states Q contains at least three elements; . . . and the SCF G is defined for the set V of all possible preference profiles. . . and the SCF is truthfully implementable in dominant strategies. . . then the SCF must be dictatorial Closely related to the Arrow theorem Has profound implications for design u u Misinformation may be endemic May only get truth-telling mechanisms in special cases

Onward from the G-S result Frank Cowell: Microeconomics n The generality of the result is striking u Market power u n 1. Way forward? Try to relax one part of G-S result Number of states u Public Goods u 2. u 3. choice problems where Q has just 2 elements? see presentation on public goods and projects All types of preferences u Contracts one could expect the phenomenon of market failure crucial to the issues of design restricted attention to a subclass of V ? see presentation on contract design Truth telling as dominant strategy u u consider a less stringent type of equilibrium? examine this now…

Nash implementation Frank Cowell: Microeconomics n n How to induce truth-telling? Dominant strategy equilibrium is demanding u u n Nash equilibrium is weaker u u u n requires everyone to tell truth… …as long as everyone else does so “I will if you will so will I…” An important implementation result: u n requires everyone to tell truth… …irrespective of what others do If a social choice function G is Nash-implementable then it is monotonic But Nash-implementation is itself limited u Economically interesting cases may still require dictatorial.

Summary Frank Cowell: Microeconomics n An issue at the heart of microeconomic policy-making: u u u n Mechanism gives insight on the problems of information u u n may be institutions which encourage agents to provide false information mechanisms may be inefficient because they provide wrong incentives Direct mechanisms help focus on the main issue u n Regulation Allocations with pure public goods Tax design use the revelation principle G-S result highlights pervasive problem of manipulability