Prerequisites Almost essential Welfare Basics Frank Cowell Microeconomics

Prerequisites Almost essential Welfare: Basics Frank Cowell: Microeconomics December 2006 Welfare: Efficiency MICROECONOMICS Principles and Analysis Frank Cowell

Welfare Principles Frank Cowell: Microeconomics n Try to find general principles for running the economy. u n We have already slipped in one notion of “desirability” u u n “Technical Efficiency” …applied to the firm What about a similar criterion for the whole economy? u u n May be more fruitful than the constitution approach. A generalised version of efficiency. Subsumes technical efficiency? And what about other desirable principles?

Overview. . . Welfare: efficiency Frank Cowell: Microeconomics Pareto efficiency Fundamental criterion for judging economic systems CE and PE Extending efficiency

A short agenda Frank Cowell: Microeconomics n n n Describe states of the economy in welfare terms. . . Use this analysis to define efficiency. Apply efficiency analysis to an economy u u n Use standard multi-agent model Same as analysed in earlier presentations. Apply efficiency concept to uncertainty u distinguish ex-ante and ex-post cases

The essential concepts Frank Cowell: Microeconomics n Social state u u n Pareto superiority u u n Describes economy completely. For example, an allocation At least as much utility for all; Strictly greater utility for some Pareto efficiency u u Uses concept of Pareto superiority. Also needs a definition of feasibility. . .

A definition of efficiency Frank Cowell: Microeconomics Link to Blocking l l l The basis for evaluating social states: vh(q) the utility level enjoyed by person h under social state q A social state q is Pareto superior to state q' if: 1. For all h: vh(q) ³ vh(q') 2. For some h: vh(q) > vh(q') Note the similarity with the concept of blocking by a coalition A social state q is Pareto efficient if: 1. It is feasible 2. No other feasible state is Pareto superior to q “feasibility” could be determined in terms of the usual economic criteria Take the case of the typical GE model.

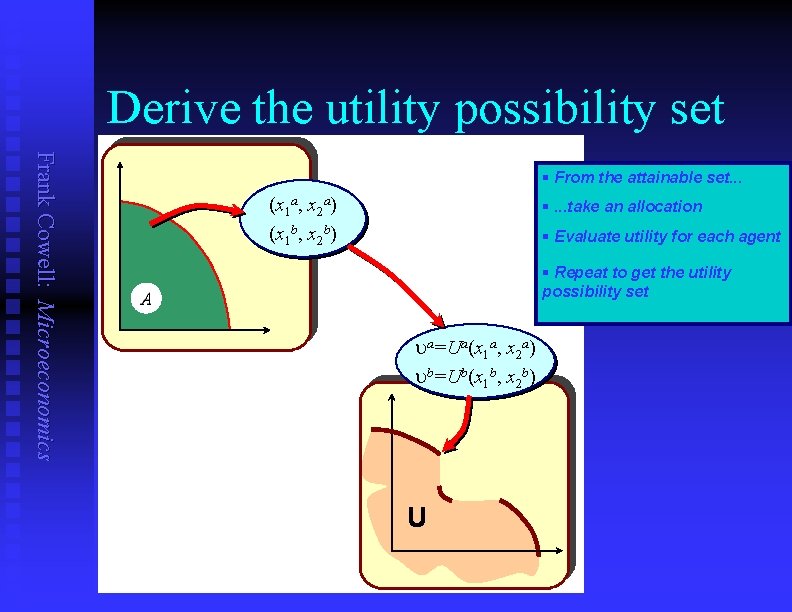
Derive the utility possibility set Frank Cowell: Microeconomics § From the attainable set. . . (x 1 a, x 2 a) (x 1 b, x 2 b) A §. . . take an allocation § Evaluate utility for each agent § Repeat to get the utility possibility set A ua=Ua(x 1 a, x 2 a) ub=Ub(x 1 b, x 2 b) U

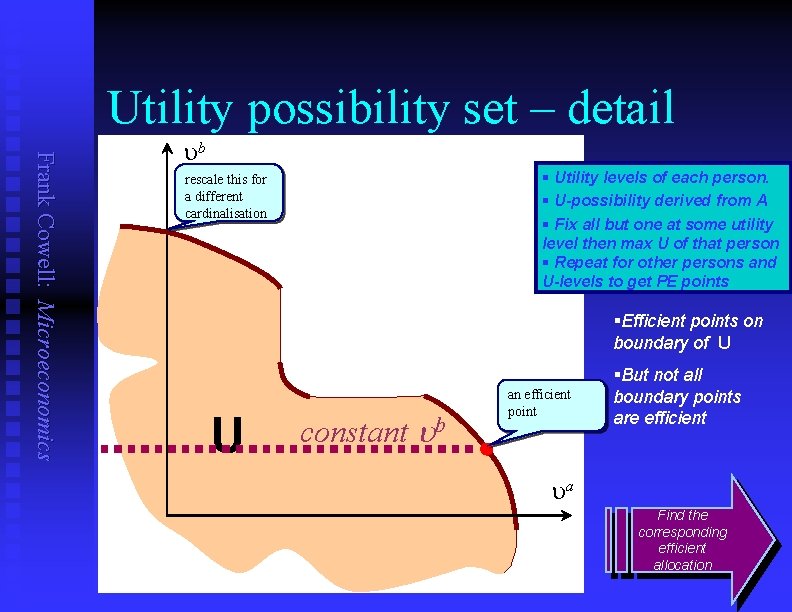
Utility possibility set – detail Frank Cowell: Microeconomics ub § Utility levels of each person. § U-possibility derived from A § Fix all but one at some utility level then max U of that person § Repeat for other persons and U-levels to get PE points rescale this for a different cardinalisation §Efficient points on boundary of U U constant ub an efficient point §But not all boundary points are efficient ua Find the corresponding efficient allocation

Finding an efficient allocation (1) Frank Cowell: Microeconomics n n Use essentially the same method. Do this for the case where u all goods are purely private u households 2, …, nh are on fixed utility levels uh n Then problem is to maximise U 1(x 1) subject to: u Uh (xh ) ≥ uh , h = 2, …, nh u Ff(qf) ≤ 0, f = 1, …, nf u xi ≤ qi + Ri , i= 1, …, n n Use all this to form a Lagrangean in the usual way…

Finding an efficient allocation (2) Frank Cowell: Microeconomics max L( [x ], [q], Lagrange multiplier for l, each m, k) : =constraint utility Lagrange multiplier for 1 1 h(x h) U (x ) + åfirm’s l [U each technology h h Lagrange multiplier for f (q f) åf mf Fmaterials balance, good i + åi ki[qi + Ri xi] where x i = å h x ih qi = åf qi f uh]

FOCs Frank Cowell: Microeconomics n n Differentiate Lagrangean w. r. t xih. If xih is positive at the optimum then: lh. Uih(xh) = ki Likewise for good j: lh. Ujh(xh) = kj Differentiate Lagrangean w. r. t qif. If qif is nonzero at the optimum then: mf. Fif(qf) = ki Likewise for good j: mf. Fjf(qf) = kj

Interpreting the FOC Frank Cowell: Microeconomics From the FOCs for any household h and goods i and j: l for every household: MRS = shadow price ratio Uih(xh) ki ———— = — Ujh (xh) kj From the FOCs for any firm f and goods i and j: l Fif(qf) for every firm: MRT = shadow price ratio ki ———— = — Fjf (qf) kj familiar example

Efficiency in an Exchange Economy Frank Cowell: Microeconomics b x 1 a x 2 b O § Alf’s indifference curves § Bill’s indifference curves § The contract curve § The set of efficient allocations is the contract curve. Allocations where MRS 12 a = MRS 12 b §Includes cases where Alf or Bill is very poor. Oa b x 2 a x 1 Apply to uncertainty

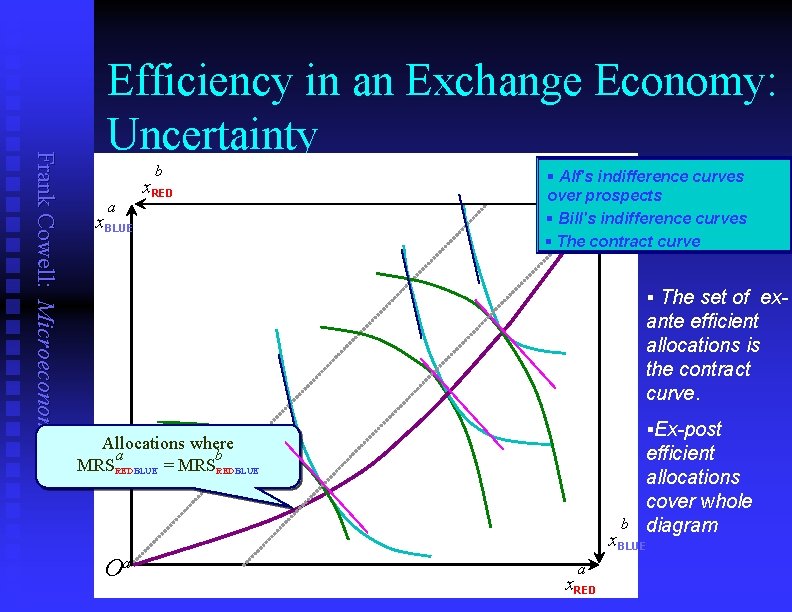
Frank Cowell: Microeconomics Efficiency in an Exchange Economy: Uncertainty b a x. RED x. BLUE § Alf's indifference curves over prospects Ob § Bill's indifference curves § The contract curve § The set of ex- ante efficient allocations is the contract curve. §Ex-post Allocations where a b MRSREDBLUE = MRSREDBLUE efficient allocations cover whole b diagram x. BLUE Oa a x. RED

Overview. . . Welfare: efficiency Frank Cowell: Microeconomics Pareto efficiency Relationship between competitive equilibrium and efficient allocations CE and PE Extending efficiency

Efficiency and equilibrium Frank Cowell: Microeconomics n n The Edgeworth Box diagrams are suggestive. Points on the contract curve… u u n So, examine connection of market with efficiency: u u u n …are efficient …could be CE allocations Will the equilibrium be efficient? Can we use the market to implement any efficient outcome? Or are there cases where the market “fails”? Focus on two important theorems

Welfare theorem 1 Frank Cowell: Microeconomics n n Assume a competitive equilibrium. What is its efficiency property? n THEOREM: if all consumers are greedy and there are no externalities then a competitive equilibrium is efficient. n Explanation: u u If they are not greedy, there may be no incentive to trade. If there are externalities the market takes no account of spillovers.

Welfare theorem 2 Frank Cowell: Microeconomics n n Pick any Pareto-efficient allocation Can we find a property distribution d so that this allocation is a CE for d? n THEOREM: if, in addition to conditions for theorem 1, there are no nonconvexities then an arbitrary PE allocation be supported by a competitive equilibrium. n Explanation: u u If “lump sum” transfers are possible then we can arbitrarily change the initial property distribution. If there are nonconvexities the equilibrium price signals could take us away from the efficient allocation. . .

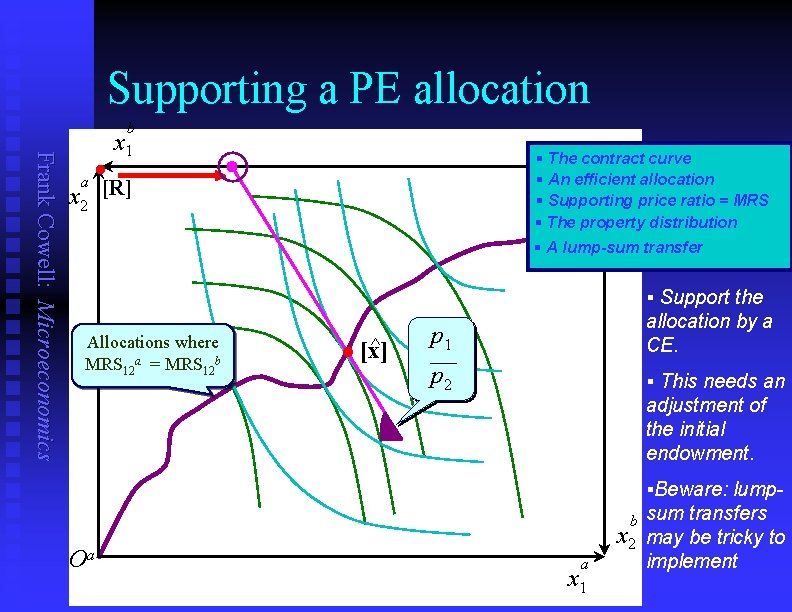
Supporting a PE allocation Frank Cowell: Microeconomics b x 1 a x 2 § The contract Ob curve § An efficient allocation § Supporting price ratio = MRS § The property distribution § A lump-sum transfer l [R] § Support the Allocations where MRS 12 a = MRS 12 b ^ l [x] p 1 allocation by a CE. p 2 § This needs an adjustment of the initial endowment. §Beware: lump- Oa b x 2 a x 1 sum transfers may be tricky to implement

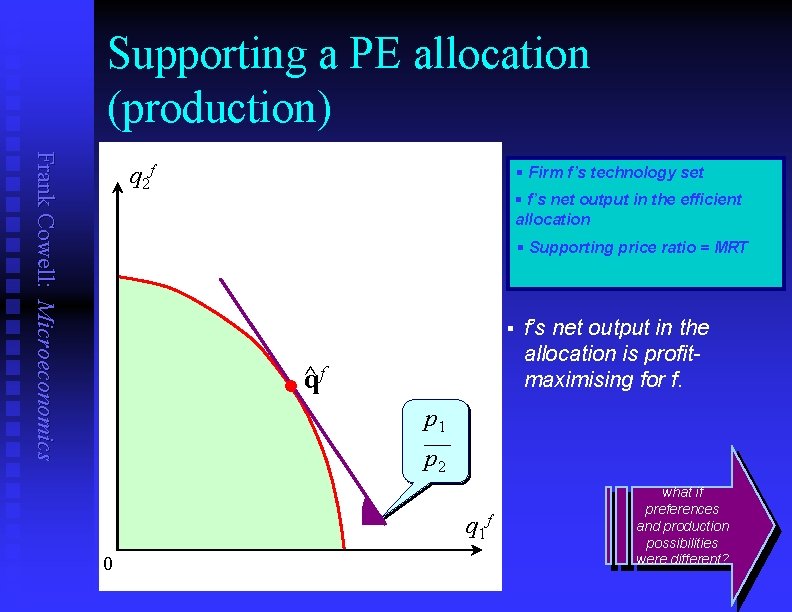
Supporting a PE allocation (production) Frank Cowell: Microeconomics q 2 f § Firm f’s technology set § f’s net output in the efficient allocation § Supporting price ratio = MRT § f ^ q l f’s net output in the allocation is profitmaximising for f. p 1 p 2 q 1 f 0 what if preferences and production possibilities were different?

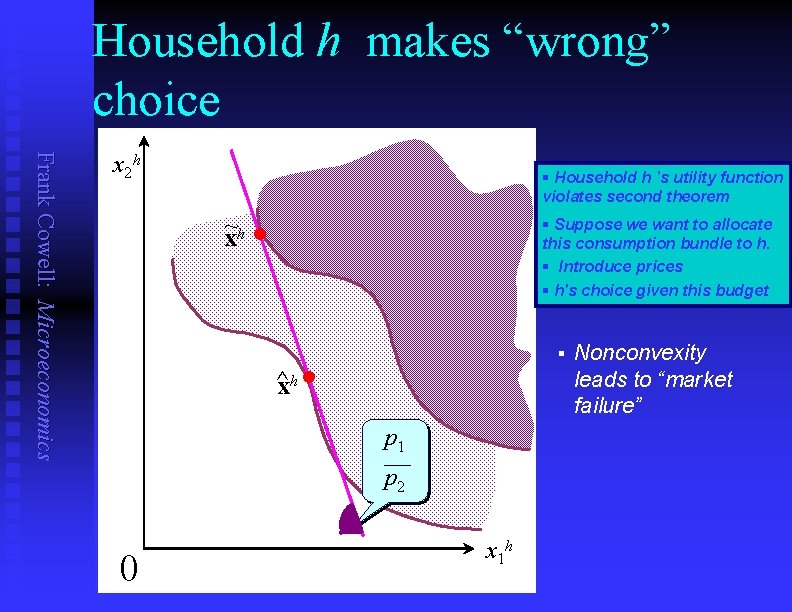
Household h makes “wrong” choice Frank Cowell: Microeconomics x 2 h § Household h ’s utility function violates second theorem ~ xh l § Suppose we want to allocate this consumption bundle to h. § Introduce prices § h's choice given this budget § ^xh l p 1 p 2 0 x 1 h Nonconvexity leads to “market failure”

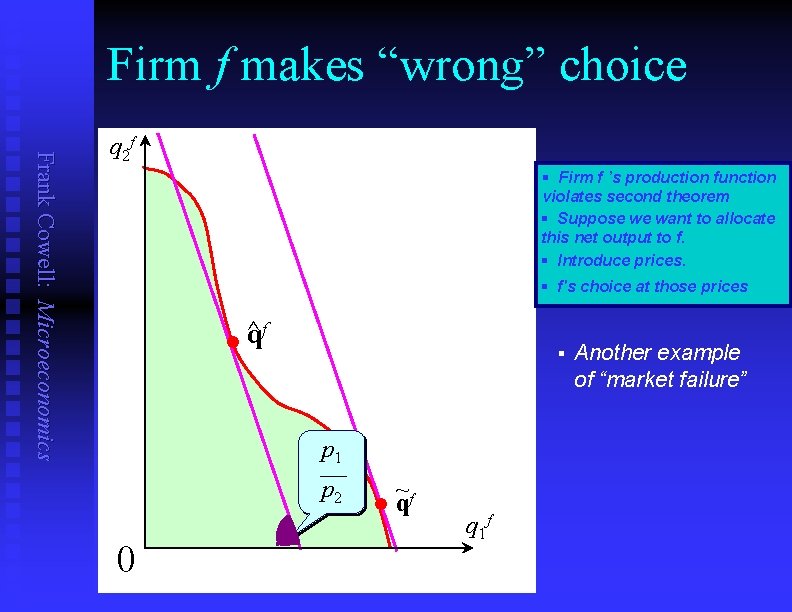
Firm f makes “wrong” choice Frank Cowell: Microeconomics q 2 f § Firm f ’s production function violates second theorem § Suppose we want to allocate this net output to f. § Introduce prices. § f's choice at those prices f ^ q l § p 1 p 2 0 ~ l qf q 1 f Another example of “market failure”

Frank Cowell: Microeconomics Competitive Failure and Efficiency n 1. The market “failures” raise two classes of problem that lead to two distinct types of analysis: The characterisation problem u u 2. The implementation problem u n n Description of modified efficiency conditions… …when conditions for the welfare theorems are not met. Design of a mechanism to achieve the allocation. These two types of problem pervade nearly all of modern micro economics. It’s important to keep them distinct in one’s mind.

Overview. . . Welfare: efficiency Frank Cowell: Microeconomics Pareto efficiency Attempt to generalise the concept of Pareto superiority CE and PE Extending efficiency

Why extend the efficiency concept? Frank Cowell: Microeconomics n Pareto efficiency is “indecisive. ” u n Pareto improvements may be elusive. u n What about the infinity of PE allocations along the contract curve? Beware the politician who insists that everybody can be made better off Other concepts may command support. u "potential" efficiency fairness u … u

Indecisiveness of PE Frank Cowell: Microeconomics ub § Construct utility-possibility set as previously § Two efficient points § Points superior to q'. §Boundary points cannot be compared on efficiency grounds v(q ) § q and q' cannot be compared on efficiency grounds v(q ) U ua A way forward?

“Potential” Pareto superiority Frank Cowell: Microeconomics n n n Define q to be potentially superior to q' if : There is a q* which is actually Pareto superior to q' q* is “accessible” from q. To make use of this concept we need to define accessibility. This can be done using a tool that we already have from theory of the consumer.

The idea of accessibility Frank Cowell: Microeconomics n Usually “q* accessible from q” means that income total in q* is no greater than in q. u n n “if society can afford q then it can certainly afford q* ” This can be interpreted as a “compensation rule” The gainers in the move from q' to q. . . get enough income to be able to compensate the losers of q' ® q. This can be expressed in terms of standard individual welfare criteria u the CV for each person

A result on potential superiority Frank Cowell: Microeconomics n n Use the terminology of individual welfare CVh(q' ® q) is the monetary value the welfare change u u u for person h… …of a change from state q' to state q …valued in terms of the prices at q n CVh > 0 means a welfare gain; CVh < 0 a welfare loss. n THEOREM: a necessary and sufficient condition for q to be potentially superior to q' is Sh CVh(q' ® q) > 0. But can we really base welfare economics on the compensating variation. . . ? n

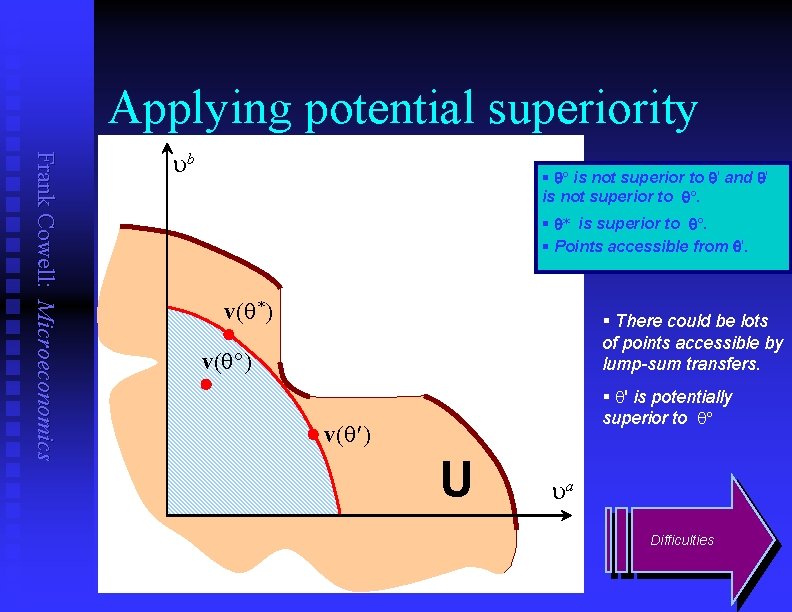
Applying potential superiority Frank Cowell: Microeconomics ub § q is not superior to q' and q' is not superior to q. § q* is superior to q. § Points accessible from q'. v(q*) § There could be lots of points accessible by lump-sum transfers. v(q ) § q' is potentially superior to q v(q ) U ua Difficulties

Problems with accessibility Frank Cowell: Microeconomics n What prices should be used in the evaluation. u u n We speak only of potential income gains. u u n compensation is not actually paid. does this matter? If no income transfer takes place… u u n those in q ? those in q' ? so that there are no consumer responses to it can we accurately evaluate gains and losses? But this isn’t the biggest problem. . .

Re-examine potential superiority Frank Cowell: Microeconomics § The process from q to q', as before. ub § The process in reverse from q' to q. points accessible from q § Combine the two. §q is potentially superior to q and … v(q ) points accessible from q v(q ) ua §q is potentially superior to q !

Extending efficiency: assessment Frank Cowell: Microeconomics n n The above is the basis of Cost-Benefit Analysis It relies on notion of “accessibility” u u n n a curious concept involving notional transfers? more than one possible definition “Compensation” is not actually paid If equilibrium prices differ substantially, the rule may produce contradictions.

What next? Frank Cowell: Microeconomics n This has formed part of the second approach to the question “how should the economy be run? ” u n n The approach covers widely used general principles Efficiency u n Neat. Simple. But perhaps limited Potential efficiency u n The first was “the constitution”. Persuasive but perhaps dangerous economics/politics A natural way forward: u u u Examine other general principles Consider problems with applying the efficiency concept Go to the third approach: a full welfare function.