Prelucrarea semnalelor an II Facultatea de Inginerie Electrica

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Prelucrarea semnalelor 2 x 14 = 28 ore curs; 1 x 14 =14 ore laborator; program: miercuri 10 -12 EA 004 laborator: EC 103 consultatii: miercuri 14 -16 EB 129 Examinare scrisa - probleme Nota finala: 0. 5 examen+0. 3 laborator + 0. 2 teme de casa (+ 0. 05 lucrari curs); Titular curs: Prof. dr. ing. Mihaela Albu Laborator: s. l. dr. ing. Felix Adochiei ing. drd. Ana Toma Prof. Mihaela Albu mihaela. albu@upb. ro

Prelucrarea semnalelor, Programa cursului: an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 1. Introducere: Repere temporale esenţiale în domeniul prelucrarii semnalelor. Semnale şi sisteme analogice si numerice. Semnale periodice si concentratori de informatie; agregarea datelor. 2. Breviar matematic. Convolutie; Transformate uzuale: Analiza Fourier; Transformate Fourier; Transformata z. 3. Simularea numerică. Convoluţia semnalelor numerice. Puterea si energia unui semnal. Definitii. 4. Filtre. Clasificare şi implementare: filtre FIR (cu faza liniara); filtre IIR (Butterworth; Bessel; Cebisev; eliptice; transformari in frecventa). Filtre numerice (MA, Windowed-sinc, specializate; metode de proiectare prin transformarea filtrelor analogice in filtre numerice). 5. Procese stochastice. Semnale aleatoare. Elemente de prelucrare numerica a semnalelor aleatoare in sisteme liniare. Prof. Mihaela Albu mihaela. albu@upb. ro

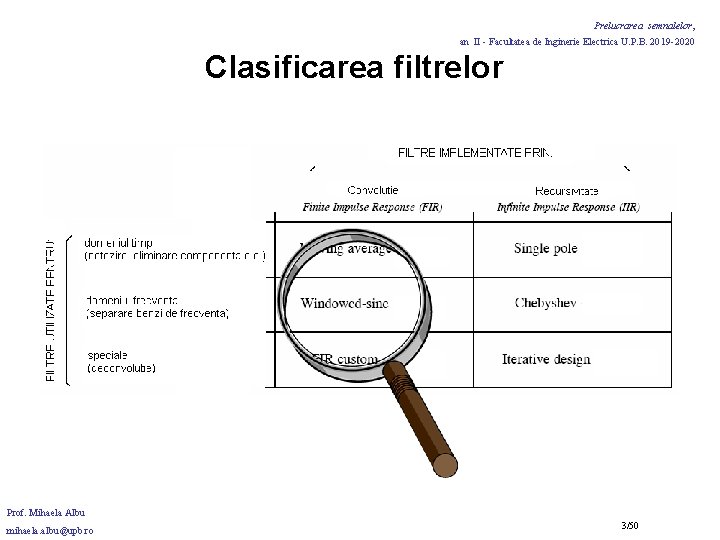
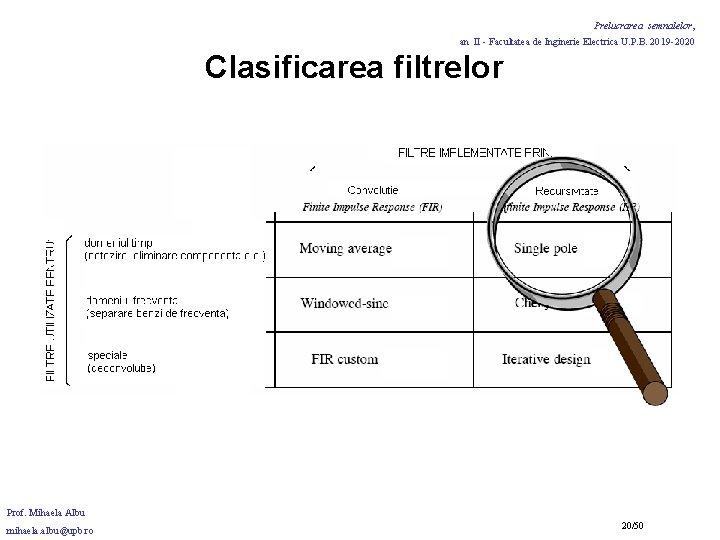
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Clasificarea filtrelor Prof. Mihaela Albu mihaela. albu@upb. ro 3/50

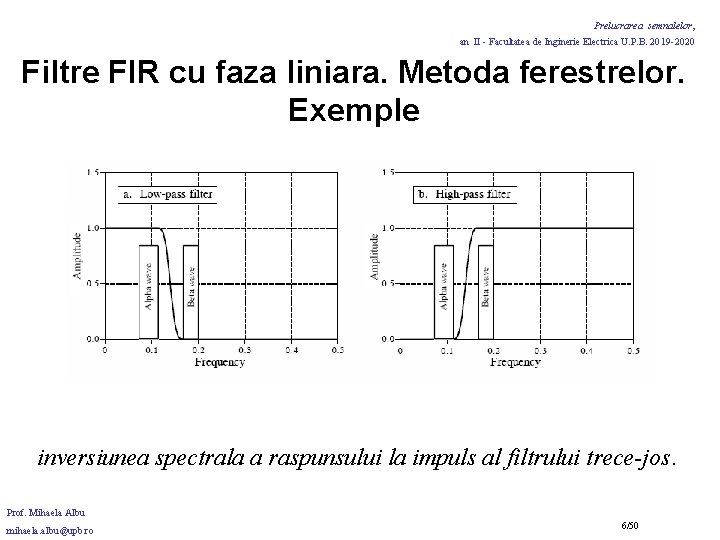
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre FIR cu faza liniara. Metoda ferestrelor. Exemple Ex. : EEG - alpha rhythm (oscilatii lente cu frecvente intre 7 si 12 Hz); - beta rhythm (oscilatii cu frecvente intre 17 si 20 Hz); Prof. Mihaela Albu mihaela. albu@upb. ro 4/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre FIR cu faza liniara. Metoda ferestrelor. Exemple • Semnalul EEG a fost amplificat (analogic), esantionat cu fs=100 Hz (esantioane pe secunda). • S-a achizitionat semnalul pe o durata de 50 s 5000 esantioane. • Scop: separare ritm alfa si beta. • Solutie: se proiecteaza un filtru numeric trece-jos cu • frecventa de taiere fc=14 Hz (=0. 14 fs); • banda de tranzitie se alege 4 Hz (=0. 04 fs); • se obtine M=101; • se alege (arbitrar!) fereastra Hamming. • se calculeaza apoi raspunsul in frecventa prin FFT asupra raspunsului la impuls. Prof. Mihaela Albu mihaela. albu@upb. ro 5/50

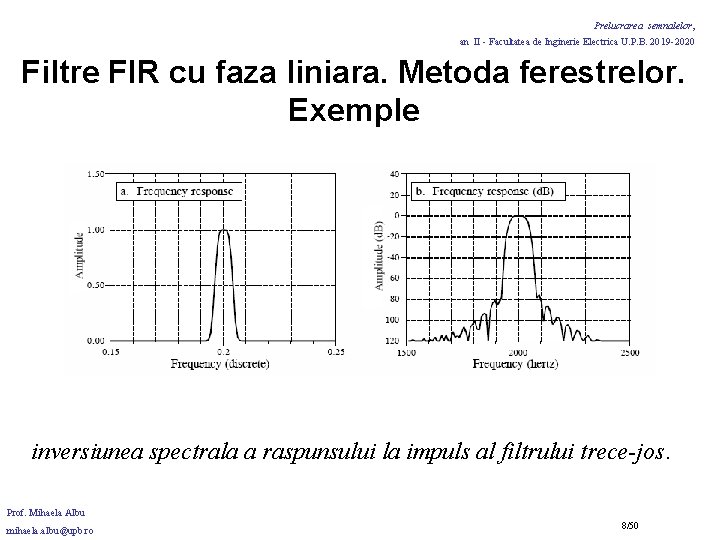
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre FIR cu faza liniara. Metoda ferestrelor. Exemple inversiunea spectrala a raspunsului la impuls al filtrului trece-jos. Prof. Mihaela Albu mihaela. albu@upb. ro 6/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre FIR cu faza liniara. Metoda ferestrelor. Exemple Ex. : proiectarea unui filtru trece-banda pentru izolarea tonului dintr-un semnal audio, atunci cind se apasa un buton al telefonului. Date: semnalul a fost esantionat cu fs=10 k. Hz si vrem sa izolam a banda de frecventa de largime 80 Hz centrata in jurul frecventei de 2 k. Hz trebuie blocate frecventele mai mici de 0. 196 si mari de 0. 204 (raportat la fs). • se alege o banda de tranzitie de 50 Hz (=0. 005 fs ) M=801; • se alege fereastra Blackman. Design: 1. Se proiecteaza doua filtre trece-jos, unul cu fc= 0. 196 si celalalt cu fc=0. 204. 2. Al doilea filtru va fi transformat (spectral inversion) obtinindu-se un filtru trece-sus. 3. Cele doua raspunsuri la impuls se aduna filtru opreste banda; 4. se aplica din nou o transformare (spectral inversion) filtrul trece-banda. Prof. Mihaela Albu mihaela. albu@upb. ro 7/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre FIR cu faza liniara. Metoda ferestrelor. Exemple inversiunea spectrala a raspunsului la impuls al filtrului trece-jos. Prof. Mihaela Albu mihaela. albu@upb. ro 8/50

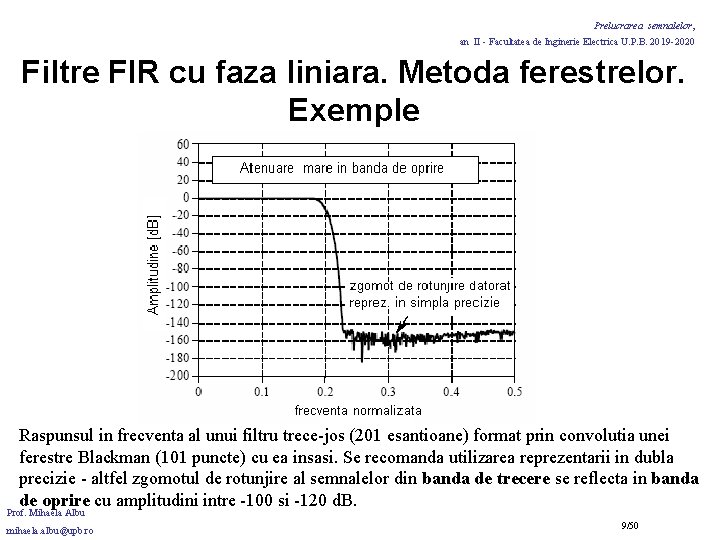
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre FIR cu faza liniara. Metoda ferestrelor. Exemple Raspunsul in frecventa al unui filtru trece-jos (201 esantioane) format prin convolutia unei ferestre Blackman (101 puncte) cu ea insasi. Se recomanda utilizarea reprezentarii in dubla precizie - altfel zgomotul de rotunjire al semnalelor din banda de trecere se reflecta in banda de oprire cu amplitudini intre -100 si -120 d. B. Prof. Mihaela Albu mihaela. albu@upb. ro 9/50

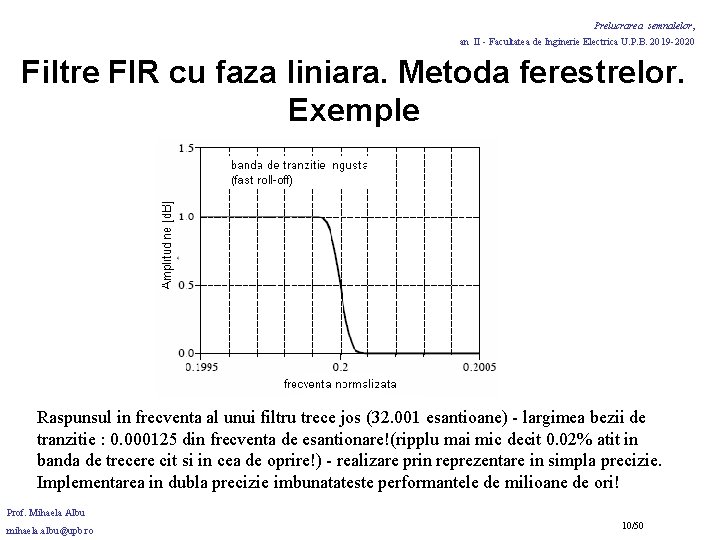
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre FIR cu faza liniara. Metoda ferestrelor. Exemple Raspunsul in frecventa al unui filtru trece jos (32. 001 esantioane) - largimea bezii de tranzitie : 0. 000125 din frecventa de esantionare!(ripplu mai mic decit 0. 02% atit in banda de trecere cit si in cea de oprire!) - realizare prin reprezentare in simpla precizie. Implementarea in dubla precizie imbunatateste performantele de milioane de ori! Prof. Mihaela Albu mihaela. albu@upb. ro 10/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Clasificarea filtrelor Prof. Mihaela Albu mihaela. albu@upb. ro 11/50

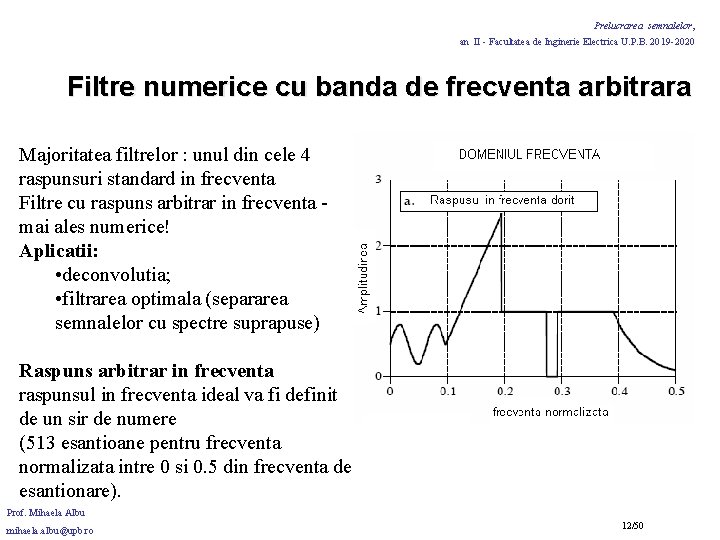
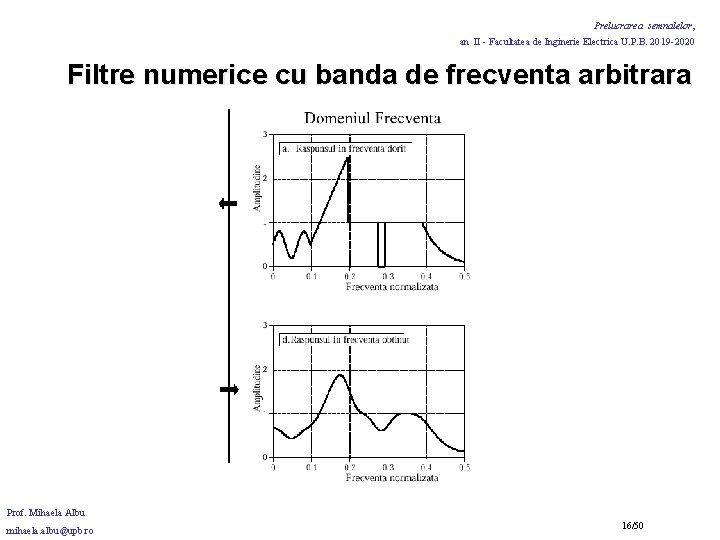
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre numerice cu banda de frecventa arbitrara Majoritatea filtrelor : unul din cele 4 raspunsuri standard in frecventa Filtre cu raspuns arbitrar in frecventa - mai ales numerice! Aplicatii: • deconvolutia; • filtrarea optimala (separarea semnalelor cu spectre suprapuse) Raspuns arbitrar in frecventa raspunsul in frecventa ideal va fi definit de un sir de numere (513 esantioane pentru frecventa normalizata intre 0 si 0. 5 din frecventa de esantionare). Prof. Mihaela Albu mihaela. albu@upb. ro 12/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre numerice cu banda de frecventa arbitrara Se specifica atit amplitudinea raspunsului in frecventa cit si faza. (un alt sir de numere arbitrare). Obs. : primul si ultimul esantion din faza (aici 0 si 512) trebuie sa fie zero! Raspunsul in frecventa poate fi specificat si prin partile reala, respectiv imaginara. Raspunsul in timp: Inverse DFT -1024 esantioane ale raspunsului la impuls (care trebuie trunchiat si alterat cu o functie fereastra). Prof. Mihaela Albu mihaela. albu@upb. ro 13/50

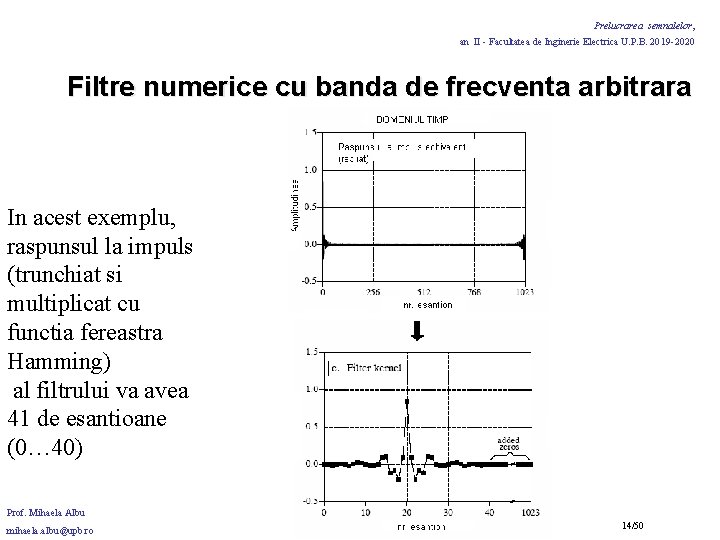
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre numerice cu banda de frecventa arbitrara In acest exemplu, raspunsul la impuls (trunchiat si multiplicat cu functia fereastra Hamming) al filtrului va avea 41 de esantioane (0… 40) Prof. Mihaela Albu mihaela. albu@upb. ro 14/50

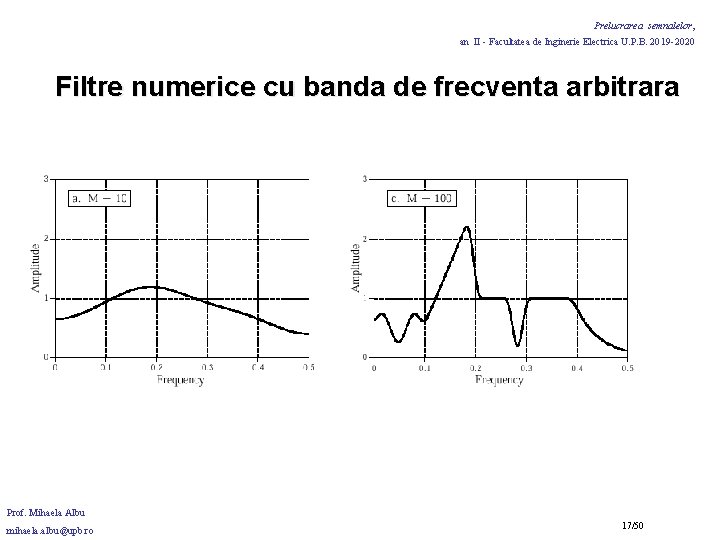
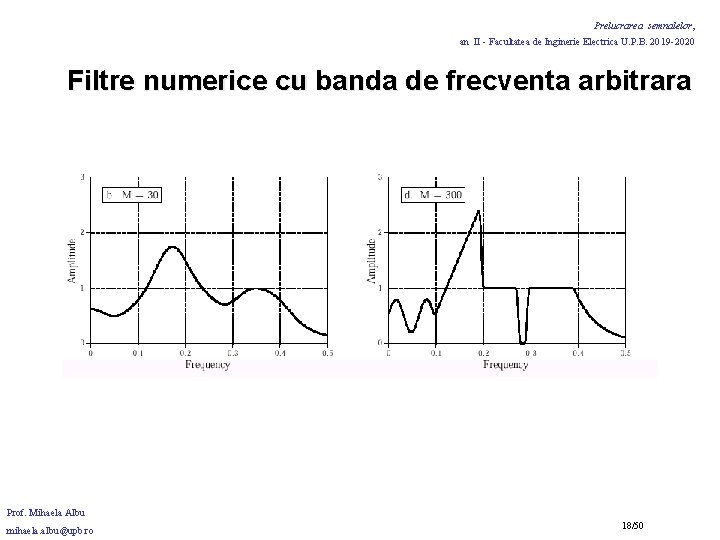
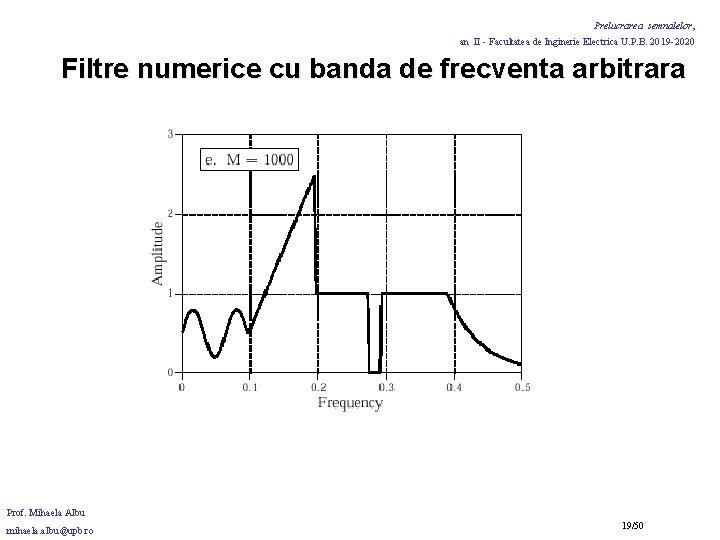
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre numerice cu banda de frecventa arbitrara Testarea raspunsului la impuls al filtrului proiectat: DFT-->raspunsul in frecventa. • Pentru o mai buna rezolutie in frecventa: se adauga zerouri la raspunsul la impuls (ex. : 1024 esantioane din 41 ale raspunsului la impuls si 983 de zerouri adaugate vor determina un raspuns in frecventa cu 513 esantioane distribuite intre 0 si 0. 5 din fs). Lungimea raspunsului la impuls determina cit de adecvat este raspunsul in frecventa al filtrului proiectat la cel al filtrului dorit. Prof. Mihaela Albu mihaela. albu@upb. ro 15/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre numerice cu banda de frecventa arbitrara Prof. Mihaela Albu mihaela. albu@upb. ro 16/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre numerice cu banda de frecventa arbitrara Prof. Mihaela Albu mihaela. albu@upb. ro 17/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre numerice cu banda de frecventa arbitrara Prof. Mihaela Albu mihaela. albu@upb. ro 18/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre numerice cu banda de frecventa arbitrara Prof. Mihaela Albu mihaela. albu@upb. ro 19/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Clasificarea filtrelor Prof. Mihaela Albu mihaela. albu@upb. ro 20/50

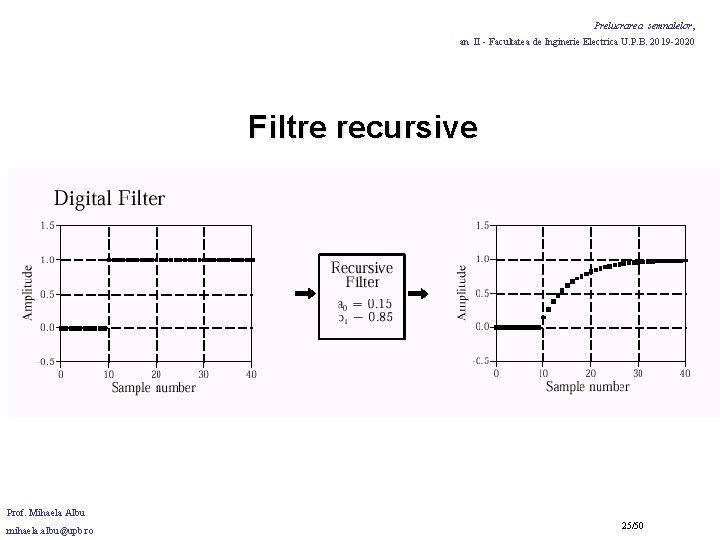
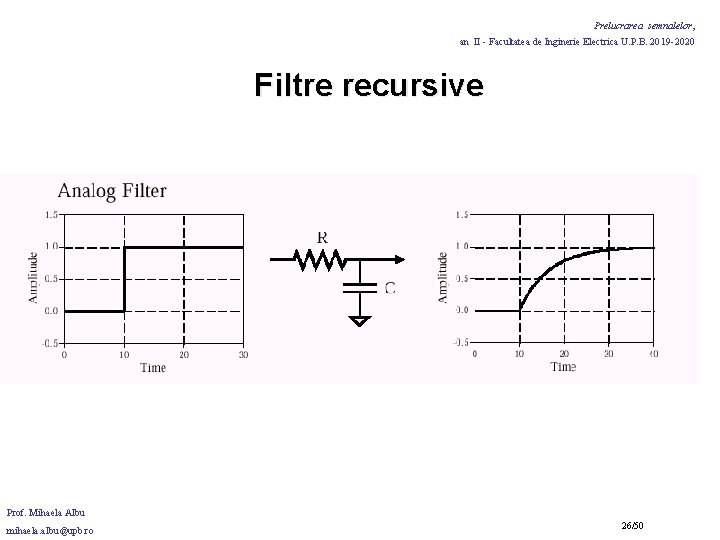
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive Filtrele recursive: mod eficient de a filtra cu filtre de lungime mare, fara a efectua convolutia! Rapide performante mai slabe flexibilitate mai mica Se mai numesc si: Infinite Impulse Response (IIR) filters, (raspunsul la impuls este format dintr-o combinatie de functii exponentiale descrescatoare) Prof. Mihaela Albu mihaela. albu@upb. ro 21/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive Ecuatia de recursivitate: Observatie: ecuatia de recursivitate in Matlab: Prof. Mihaela Albu mihaela. albu@upb. ro 22/50

Filtre recursive Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Relatia dintre coeficientii recursivi si raspunsul la impuls al filtrului descrisa de transformata z: • converteste coeficientii recursivi in raspunsul in frecventa al filtrului, • permite realizarea de combinatii de filtre in cascada si a etajelor paralele de filtrare • permite proiectarea de sisteme recursive care simuleaza Prof. Mihaela Albu 23/50 comportarea filtrelor analogice mihaela. albu@upb. ro

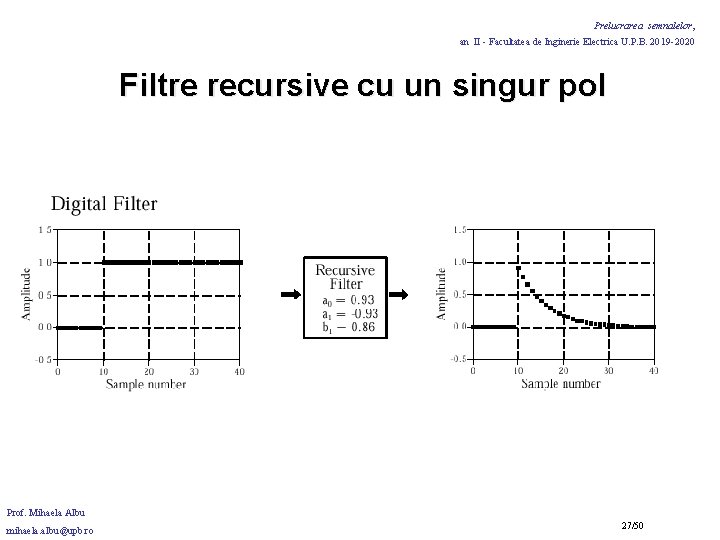
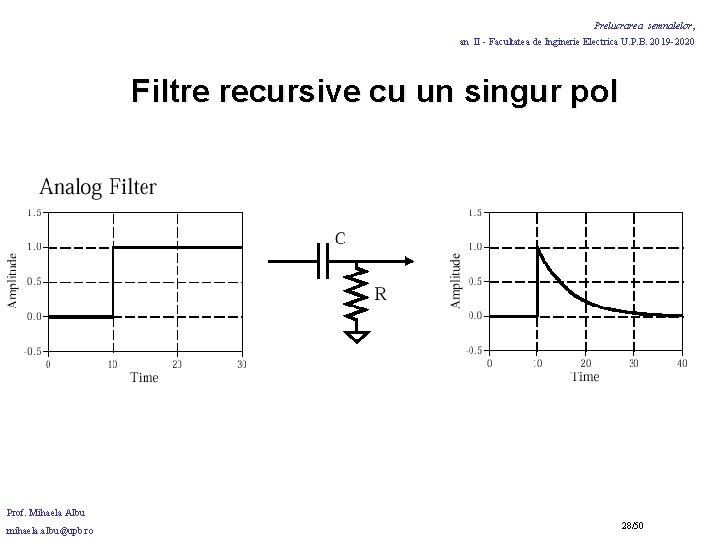
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive cu un singur pol filtrul recursiv cu un singur pol - ecuatie cu numai doi coeficienti ex: a = 0. 15 b =0. 85 este complet similar cu un filtru analogic trece -jos (RC) ! Se pot crea o multime de raspunsuri doar variind citiva parametri: ex. : a = 0. 93 a 1 =- 0. 93 b = 0. 86 simuleaza un filtru trece-sus RC. Prof. Mihaela Albu mihaela. albu@upb. ro 24/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive Prof. Mihaela Albu mihaela. albu@upb. ro 25/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive Prof. Mihaela Albu mihaela. albu@upb. ro 26/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive cu un singur pol Prof. Mihaela Albu mihaela. albu@upb. ro 27/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive cu un singur pol Prof. Mihaela Albu mihaela. albu@upb. ro 28/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive cu un singur pol Se executa rapid, dar pot produce surprize! Exemplu de generalizare: Filtru trece-jos: Filtru trece-sus: Prof. Mihaela Albu mihaela. albu@upb. ro 29/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive cu un singur pol Caracteristicile filtrului cu un pol sunt determinate de valorile parametrului x 0<x<1 x reprezinta valoarea cu care se micsoreaza doua esantioane adiacente in raspuns. Cu cit x este mai mare, cu atit descresterea este mai lenta pentru x>1 filtrul devine instabil x se poate determina din constanta de timp dorita daca d este numarul de esantioane necesar raspunsului pentru a descreste la 1/e din valoarea initiala (constanta de timp), atunci: x=e-1/d Prof. Mihaela Albu mihaela. albu@upb. ro 30/50

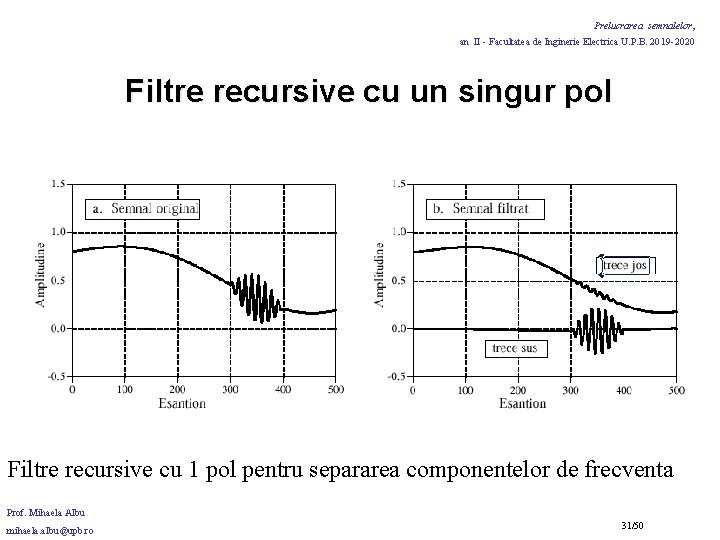
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive cu un singur pol Filtre recursive cu 1 pol pentru separarea componentelor de frecventa Prof. Mihaela Albu mihaela. albu@upb. ro 31/50

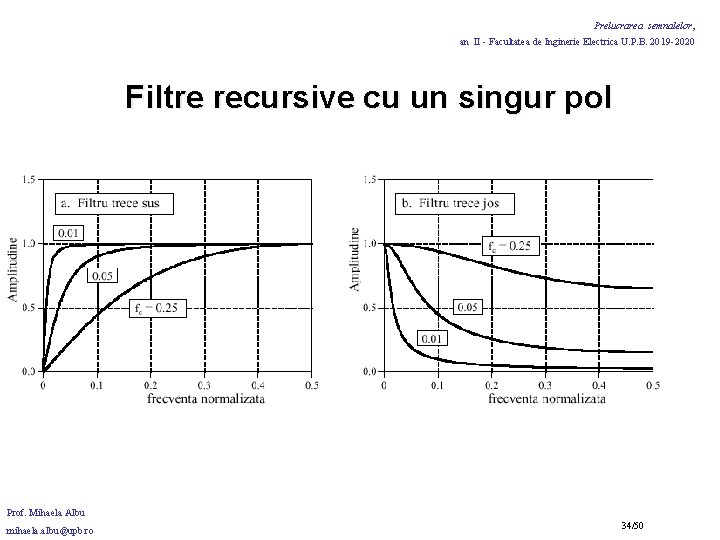
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive cu un singur pol Relatia dintre x si frecventa de taiere (definita la -3 d. B): x=e-2 fc --> trei moduri de a determina coeficientii a si b ai filtrului recursiv de ordinul 1: • din constanta de timp • din frecventa de taiere • prin alegere directa Prof. Mihaela Albu mihaela. albu@upb. ro 32/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive cu un singur pol In fig. urmatoare: raspunsul in frecventa al mai multor filtre recursive cu un pol (de ordinul 1) (obtinere: impuls delta la intrare, apoi aplicarea FFT raspunsului la impuls) Prin definitie, raspunsul la impuls este infinit lung; practic: descreste sub eroarea de rotunjire in simpla precizie dupa 15 -20 constante de timp. Ex. : ct. de timp d=6. 63 esantioane raspunsul la impuls poate fi trunchiat la 128 esantioane. Obs. : filtrele recursive de ordinul 1 nu au performante bune in separarea benzilor de frecventa! Prof. Mihaela Albu mihaela. albu@upb. ro 33/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive cu un singur pol Prof. Mihaela Albu mihaela. albu@upb. ro 34/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive cu un singur pol Prof. Mihaela Albu mihaela. albu@upb. ro 35/50

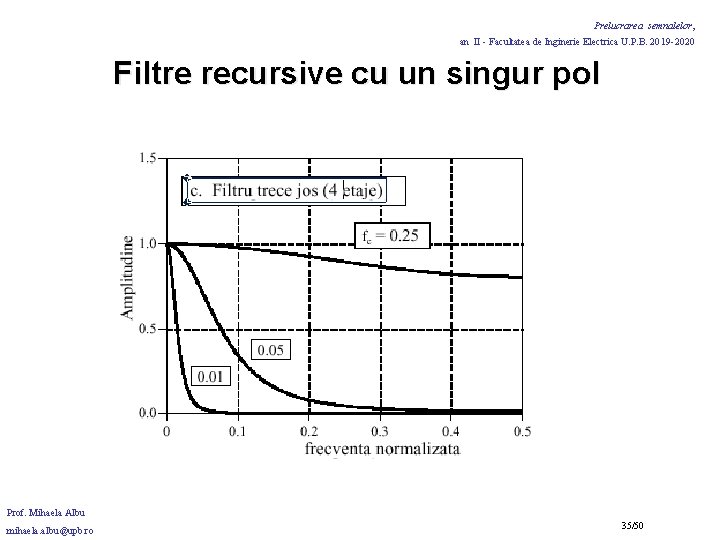
Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive cu un singur pol Solutie: imbunatatire (usoara) prin utilizarea filtrelor recursive in cascada! Doua moduri de cascadare: 1. Se trece semnalul prin filtru de citeva ori. 2. Se utilizeaza transformata z pentru a gasi coeficientii corespunzatori etajelor de filtrare Obs. in figura c), se utilizeaza 4 etaje de amplificare si atenuarea in banda de oprire este mult mai buna DAR banda de tranzitie foarte larga (slow roll-off). Performante mai bune in frecventa filtrele Cebisev (Chebyshev) Prof. Mihaela Albu mihaela. albu@upb. ro 36/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Filtre recursive cu un singur pol raspunsul in frecventa al mai multor filtre recursive cu un pol (de ordinul 1): cum? impuls delta la intrare, apoi aplicarea FFT raspunsului la impuls Prin definitie, raspunsul la impuls este infinit lung; practic: descreste sub eroarea de rotunjire in simpla precizie dupa 15 -20 constante de timp. Ex. : ct. de timp d=6. 63 esantioane raspunsul la impuls poate fi trunchiat la 128 esantioane. Obs. : filtrele recursive de ordinul 1 nu au performante bune in separarea benzilor de frecventa! Prof. Mihaela Albu mihaela. albu@upb. ro 37/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Probleme 1. Fie y[n]=0. 5(x[n] + x[n-1]) + y[n-1], n 0 a) găsiţi H(z) a sistemului descris de ecuaţia de recursivitate de mai sus; b) determinaţi răspunsul la impuls al sistemului, h[n] 2. Fie sistemul IIR descris de: y[n] = a 1 y[n-1] + a 2 y[n-2] + a 1 y[n-1] + x[n], n 0 a) găsiţi H(z) a sistemului descris de ecuaţia de recursivitate de mai sus; b) determinaţi condiţiile pe care trebuie să le satisfacă a 1 şi a 2 pentru ca sistemul să fie stabil. 3. Fie filtrul MA de lungime L=3. Calculaţi banda de 6 d. B dacã frecvenţa de eşantionare este 42 k. Hz. Prof. Mihaela Albu mihaela. albu@upb. ro 38/50

Prelucrarea semnalelor, an II - Facultatea de Inginerie Electrica U. P. B. 2019 -2020 Intrebari / semnalare erori (!). Prof. Mihaela Albu mihaela. albu@upb. ro albu@ieee. org