Preliminaries Language Set of Strings CSC 361 Preliminaries

Preliminaries Language: Set of Strings CSC 361 Preliminaries 1

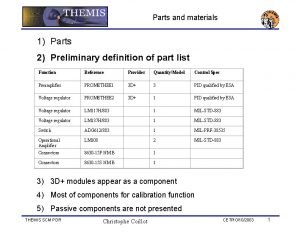
n Specification and recognition of languages n Sets n n n Strings n n Operations Defining sets (inductively) Proving properties about sets (using induction) Defining functions on sets (using recursion) Proving properties about functions (using induction) Operations Languages : set of strings n CSC 361 Operations Preliminaries 2

Representation of Sets n Set: collection of objects n Finite : can use enumeration n n E. g. , {a, b, c} Infinite : requires describing an infinite characteristic of members using finite terms n CSC 361 E. g. , { n e N | even(n) / square(n) } Preliminaries 3

Sets: Examples • Sets are denoted by { <collection of elements> } • Examples: v{0, 1, 2, …} “the empty set” “the set consisting of the elements a and b” “the set consisting of the empty set” “the set consisting of the first 100 natural numbers” “the set consisting of all natural numbers” v{0, 2, 4, …} v{2 n | n } “the set of all natural pair numbers” v{} v{a, b} v{{}} v{1, 2, …, 100} CSC 361 Preliminaries 4

Operations on Sets Set Inclusion and Set Equality Definition: • Given 2 sets, A and B, A is contained in B, denoted by A B, if every element in A is also an element in B True or false: v{e, i, t, c} {a, b, …, z} true v for any set A, A A true v for any set A, A {A} false Definition: • Given 2 sets A and B, A is equal to B, denoted by A = B, if A B and B A CSC 361 Preliminaries 5

Operations on Sets n Review: n n n Member Union Intersection Subset Powerset Cartesian product CSC 361 Preliminaries 6

Operations on Sets n Set Difference n De. Morgan’s Laws CSC 361 Preliminaries 7

Operations on Sets Cartesian Product • Definition: Given two sets, A and B, the Cartesian product of A and B, denoted by A B, is the following set: {(a, b) | a A and b B} pair or 2 -tuple Examples: • What is: {1, 2 , 3} {a, b} = {(1, a), (1, b), (2, a), (2, b), (3, a), (3, b)} • True or false: {(1, a), (3, b)} {1, 2 , 3} {a, b} true • True or false: {1, 2, 3} {1, 2 , 3} {a, b} false CSC 361 Preliminaries 8

Operations on Sets Cartesian Product of More Than 2 Sets Definition: Given three sets, A, B and C, the Cartesian product of A, B, and C denoted by A B C, is the following set: {(a, b, c) | a A, b B, c C} Triple or 3 -tuple Definition. (x, y, z) = (x’, y’, z’) only if x = x’, y = y’ and z = z’ These definitions can be extended to define the Cartesian product: A 1 A 2 … An and equality between n-tuples CSC 361 Preliminaries 9

Operations on Sets • Some Cartesian product problems to try out: • What is: {1, 2 , 3} {a, b} { , } = • What is the form of the set A B C D • What is the form of the set A B (C D) • What is the form of the set (A B ) (C D) CSC 361 Preliminaries 10

Partition of a Set X The set of subsets of X is a partition of X (1) “covers all subsets” (2) “pair-wise disjoint” iff Collectively Exhaustive / Mutually Exclusive CSC 361 Preliminaries 11

Examples n Set of Natural numbers is partitioned by “mod 5” relation into five “equivalence classes”: { {0, 5, 10, …}, {1, 6, 11, …}, {2, 7, 12, …}, {3, 8, 13, …}, {4, 9, 14, …} } n “String length” can be used to partition the set of all bit strings. { {}, {0, 1}, {00, 01, 10, 11}, {000, …, 111}, … } CSC 361 Preliminaries 12

Relations Definition: Given two sets, A and B, A relation R is any subset of A B. In other words, R A B • Relations are used to describe how elements of different sets interact v. Question: What does the relation A B indicate? v. Examples of relations Simple: • {(c, s) | c is a class at KU, s is a student at KU, AND s is in C } CSC 361 Preliminaries 13

Relations Example: Let I be the set of all classroom instructors at Kutztown n Let S be the set of all students at Kutztown n Then, we can define the relation Students of an Instructor, over I x S, as follows: Students of an Instructor= {(i, s) | i I, s S, s is in a course of instructor i} Questions: 1. Does this relation represent an equivalence relation? 2. Suppose this instructor teaches courses c 1, c 2, and c 3. Would the sets Students in instructor i’s course, for courses c 1, c 2, and c 3, be disjoint? n CSC 361 Preliminaries 14

Equivalence Relations A relation R is an equivalence relation if R is reflexive, symmetric, and transitive Relation R is: • reflexive if (a, a) R for each a in the language • symmetric if when (a, b) R then (b, a) R • transitive if (a, b) R and (b, c) R, then (a, c) R Equivalence relations are generalizations of the equality relation x {(1, 2), (1, 3), …, (2, 3), (2, 4), …} “the relation x < y” {(a, b) | a and b are males between 35 and 40 years old} CSC 361 Preliminaries 15

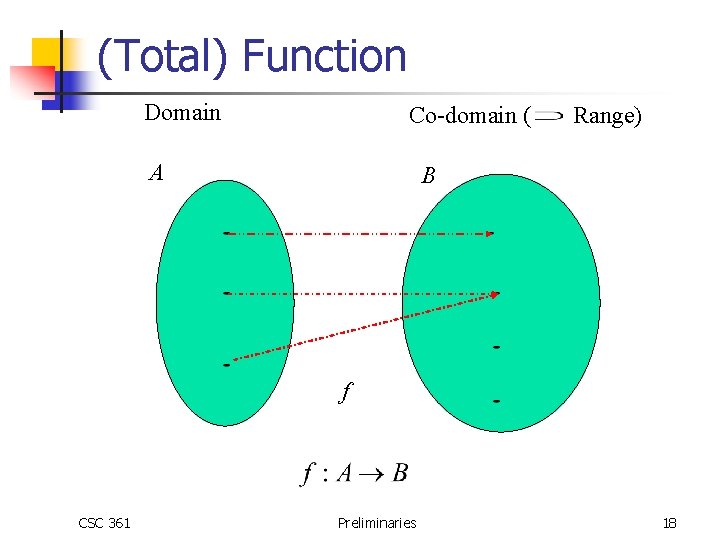
Functions Definition: A function f from a set A to a set B, denoted by f: A B , is rule of correspondence between A and B such that there is a unique element in B assigned to each element in A i. e. for each a A there is one and only one b B such that (a, b) f Note: • A is the domain of f • B is the range of f Question: Is the following relation also a function from the set of KU classes to the set of KU students? {(c, s) | c is a class at KU, s is a student at KU, AND s is in C } CSC 361 Preliminaries 16

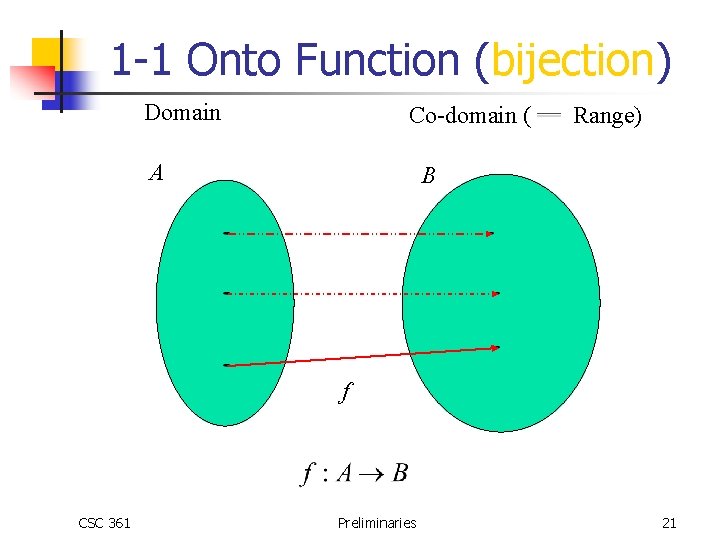
Functions n Kinds of Functions n Total n n One to one (injection) n n CSC 361 Total, and each mapping from domain to range is unique Onto (surjection) n n All domain elements map to an element in the range All elements of the range are mapped to from a domain element 1 -1 & Onto (bijection) Preliminaries 17

(Total) Function Domain Co-domain ( A Range) B f CSC 361 Preliminaries 18

One to One Function (injection) Domain Co-domain ( A Range) B f CSC 361 Preliminaries 19

Onto Function (surjection) Domain Co-domain ( A Range) B f CSC 361 Preliminaries 20

1 -1 Onto Function (bijection) Domain Co-domain ( A Range) B f CSC 361 Preliminaries 21

Inductive Definitions n Constructive n Example n Set of natural numbers N = {0, 1, 2, 3, …} n Finite representation in terms of Seed element: zero Closure Operation: successor function {0, s(0), s(s(0)), s(s(s(0))), …} n Imposes additional structure on the domain. CSC 361 Preliminaries 22

n n n Basis case: Recursive step: Closure: only if it can be obtained from 0 by a finite number of applications of the operation s. (* Minimality condition to uniquely determine N *) CSC 361 Preliminaries 23

Languages n n A language can be specified as a set of strings. Languages are classified by how they can be formed n n Regular languages are the most constrained Others n n n CSC 361 Context-free Context-sensitive Recursively enumerable Preliminaries 24

Language Semantics - Syntax n Regular sets/languages n Generator n n Recognizer n n Regular Expressions, Regular Grammars Finite State Automata Context-free languages n Generator n n Context-free Grammar Recognizer n CSC 361 Push-down Automata Preliminaries 25