Predstavljanje nesavrenog znanja Nesavreno znanje izraeno kroz neizrazitost

Predstavljanje nesavršenog znanja Nesavršeno znanje izraženo kroz neizrazitost NEIZRAZITA LOGIKA I TEORIJA MOGUĆNOSTI 1

Predstavljanje nesavršenog znanja NEIZRAZITA LOGIKA I TEORIJA MOGUĆNOSTI Lotfy Zadeh, 1965 Modelira nejasnost, nepreciznost. U inženjerstvu često nalazimo oblik pravila: AKO: u 1 vrlo toplo i u 2 manje-više nisko, TADA: podesi v 1 vrlo visoko Gdje su: toplo, nisko, visoko (umjesto precizno 73 C): Lingvističke varijable vrlo, manje-više: Modifikatori varijabli Sustav neizrazite logike u upravljanju procesima: izrazito->neizrazito izraziti vektor neizr. zaključivanje neizrazito->izrazito izraziti skalar 2

Predstavljanje nesavršenog znanja: Teorija neizrazitih skupova A E ; A je podskup E, gdje je E skup koji definira domenu razmatranja. Pripadnost elementa označujemo: x A Izražavanje pripadnosti preko karakteristične funkcije (funkcije pripadnosti): A(x) = 1; ako x A A(x) = 0; ako x A Npr: E = {x 1, x 2, x 3, x 4, x 5} ; domena, okvir razmatranja A = { x 2, x 3, x 4} Tada: A(x 1) = 0, A(x 2) = 1, A(x 3) = 1, A(x 4) = 1, A(x 5) = 0 ili drugačije: A = {x 1/0, x 2/1, x 3/1, x 4/1, x 5/0} Skup je izrazit ako karakteristična funkcija može poprimiti diskretnu vrijednost 0 ili 1. 3

Predstavljanje nesavršenog znanja: Teorija neizrazitih skupova Skup je neizrazit ako karakteristična funkcija može poprimiti bilo koju vrijednost iz intervala [0, 1]. Primjer neizrazitog diskretnog skupa malih (lingvistička varijabla) cijelih brojeva: A~ = {0/1, 1/1, 2/1, 3/0. 8, 4/0. 6, … } Interpretacija: 0, 1 i 2, potpuno pripadaju skupu, 3 pripada velikim dijelom, 4 pripada nešto manje nego 3, … n n n Jedna moguća oznaka za neizrazit skup (nije standard): A ~ Vrijednosti karakteristične funkcije odabrane su subjektivno. Lingvistička varijabla opisana je vrijednostima karakteristične funkcije. 4

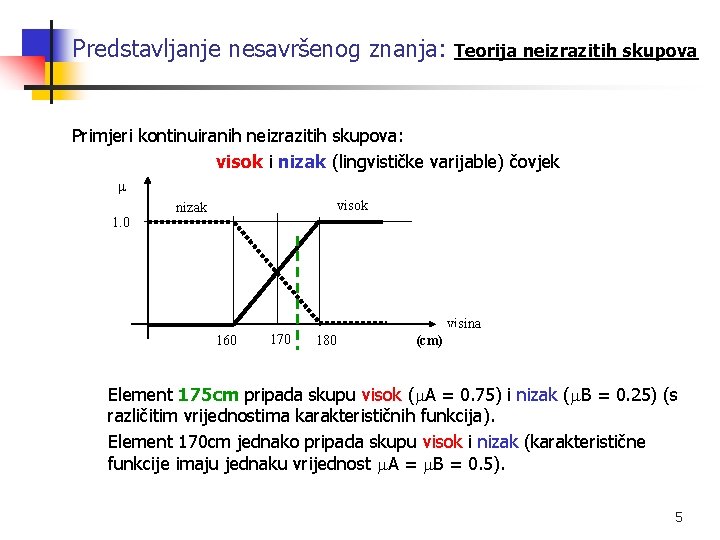
Predstavljanje nesavršenog znanja: Teorija neizrazitih skupova Primjeri kontinuiranih neizrazitih skupova: visok i nizak (lingvističke varijable) čovjek 1. 0 visok nizak visina 160 170 180 (cm) Element 175 cm pripada skupu visok ( A = 0. 75) i nizak ( B = 0. 25) (s različitim vrijednostima karakterističnih funkcija). Element 170 cm jednako pripada skupu visok i nizak (karakteristične funkcije imaju jednaku vrijednost A = B = 0. 5). 5

Predstavljanje nesavršenog znanja: Teorija neizrazitih skupova Operacije s neizrazitim skupovima (sve oznake za skupove odnose se na neizrazite skupove, tj, A = A~, B = B~ , A' je komplement neizrazitog skupa) A = B, akko A(x) = B(x), za x E A B , akko A(x) B(x), za x E A' (x) = 1 - A(x) (A B) = min[ A, B] (A B) = max[ A, B] A (B C) = (A B) (A C) (A B) C = A (B C) A B=B A A A=A A 0=0 A E=E (A B)' = (A' B') A A' 0 A A' E (jednakost) (podskup) (komplement) (presjek) (unija) (distributivnost) (asocijacija) (komutacija) (De. Morgan) 6

Predstavljanje nesavršenog znanja: Teorija neizrazitih skupova Modifikatori lingvističkih varijabli (modificiraju karakterističnu funkciju) "vrlo" (koncentracija): con(A~) = [ A(x)]2 "manje-više" (dilatacija): dil(A~) = [ A(x)]1/2 1. 0 dil con n Modifikatora lingvističkih varijabli ima mnogo. Modifikatori lingvističkih varijabli nisu standardizirani. Gornji izrazi su uobičajeni. 7

Predstavljanje nesavršenog znanja Neizrazita logika Svaka atomička izjava preslikava se u karakterističnu funkciju (diskretnu ili kontinuiranu). Npr: P: "x je mali cijeli broj. “, preslikava se u karakterističnu funkciju (A). Q: "Ivan je visok. “, preslikava se u karakterističnu funkciju (B). Logički operatori (izvode se nad vrijednostima karakterističnih funkcija i rezultiraju u novoj karakterističnoj funkciji): Negacija: Konjunkcija: Disjunkcija: ( A) = 1 - (A) (A B) = min[ (A), (B)] (A B) = max[ (A), (B)] (sve oznake skupova odnose se na neizrazite skupove) 8

Predstavljanje nesavršenog znanja Neizrazita logika Implikacija: Klasična logika: (P Q) = (P ( Q)) Neizrazita logika: (A B) = max[(1 - (A)), (B)] = 1 - min[ (A), (1 - (B))] Postoji mnogo izvedenica koje su logički ekvivalentne. 9

Predstavljanje nesavršenog znanja Neizrazita logika: Problem implikacije: (A B) = 1 - min[ (A), (1 - (B))] Implikacija preslikava pravilo: Ako A tada B. Ako je domena B konačna, i implikacija mora rezultirati u nečem konačnom. Protuprimjer (domena implikacije je beskonačna): A Predložene su inženjerske definicije implikacije: B 1. (A B) = min [ (A) , (B) ] min, Mamdani, 1974 (A B) 2. (A B) = [ (A) · (B)] produkt, Larsen, 1980 10

Predstavljanje nesavršenog znanja Neizrazita logika i poopćeni “Modus ponens” Klasična logika: A A B B ; pri čemu A u formulama moraju biti striktno jednaki. Neizrazita logika: A 1 A 2 B 1 B 2 ; pri čemu A 1 i A 2, te B 1 i B 2 su slični neizraziti skupovi. Premise kao neizraziti skupovi predstavljene su karakterističnim funkcijama, a zaključak je njihova kompozicija: (B 2) = (A 1) (A 2 B 1) Kompozicija se može definirati na razne načine. Npr. (proširuje se na n sudova): (B 2) = max [min ( (A 1) , (A 2 B 1))] (B 2) = max [ (A 1) · (A 2 B 1)] (max-min, Zadeh) (max- produkt) 11

Predstavljanje nesavršenog znanja Poopćeni Modus Ponens – Primjer s neizrazitim diskretnim skupovima: Neka je domena razmatranja skup: E = {1, 2, 3, 4} Premise: A: x je mali cijeli broj. B: y i x su približno jednaki. Zaključak: y je ? (traži se karakteristična funkcija zaključka) Neka je subjektivno karakteristična funkcija premise A: A = {1/1, 2/0. 6, 3/0. 2, 4/0} B: karakterističnu funkciju definiramo kao matricu koja ima vrijednosti 1 ako su vrijednosti x i y jednake, 0. 5 ako su susjedne (malo se razlikuju) i 0 ako su udaljene. 1 2 3 4 1 1 0. 5 0 0 2 0. 5 1 0. 5 0 3 0 0. 5 1 0. 5 4 0 0 0. 5 1 12

Predstavljanje nesavršenog znanja Poopćeni Modus Ponens – Primjer s neizrazitim diskretnim skupovima: Kompoziciju računamo prema max-min pravilu (Zadeh): (A) (B) = max { min [(1 , 1 ), (0. 6, 0. 5), (0. 2, 0), (0, 0) ], min [(1, 0. 5), (0. 6, 1), (0. 2, 0. 5), (0, 0) ], min [(1, 0), (0. 6, 0. 5), (0. 2, 1), (0, 0. 5)], min [(1, 0), (0. 6, 0), (0. 2, 0. 5), (0, 1) ] } = = max { [1, 0. 5, 0, 0], [0. 5, 0. 6, 0. 2, 0], [0, 0. 5, 0. 2, 0], [0, 0, 0. 2, 0] } = = {1, 0. 6, 0. 5, 0. 2} Zaključak: y je također mali cijeli broj (nešto malo više nego x). 13

Predstavljanje nesavršenog znanja Teorija mogućnosti temeljena na neizrazitoj logici Vjerojatnost (engl. probability) daje mjeru (šansu) da će se događaj realizirati. Mogućnost (engl. possibility) daje mjeru (vrijednost karakteristične funkcije) pripadnosti skupu. Primjeri: p – vjerojatnost - vrijednost karakteristične funkcije (mjera pripadnosti skupu) Na boci s vodom piše: p(pitka: voda) = 0. 9 (pitka_voda) = 0. 9 Na hladnjaku piše: p(pivo_je_u_hladnjaku) = 0. 5 Postoji 10% šanse da voda nije za piće. Voda nije savršena, ali se može piti. U 50% slučajeva nema piva u hladnjaku. U hladnjaku je pola boce piva. 14

Predstavljanje nesavršenog znanja Zaključivanje s neizrazitim pravilima (Ekspertni sustavi temeljeni na neizrazitoj logici): izrazito->neizrazito neizr. zaključivanje neizrazito->izrazito izraziti vektor izraziti skalar Neka u ekspertnom sustavu postoji baza znanja sa slijedećim pravilima: rule 1: rule 2: rule 3: rule 4: if x is low and y is low then z is high if x is low and y is high then z is low if x is high and y is low then z is low if x is high and y is high then z is high Uočavamo da postoji 6 lingvističkih varijabli bez modifikatora: x_low, x_high, y_low, y_high, z_low, z_high U prvom koraku potrebno je za svaku lingvističku varijablu definirati odgovarajuću karakterističnu funkciju. 15

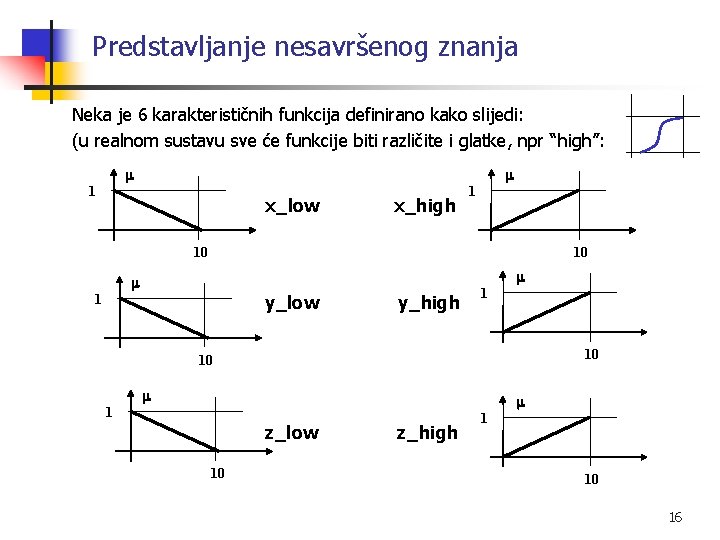
Predstavljanje nesavršenog znanja Neka je 6 karakterističnih funkcija definirano kako slijedi: (u realnom sustavu sve će funkcije biti različite i glatke, npr “high”: 1 x_low x_high 1 10 10 y_low 1 y_high 1 10 10 1 z_low 10 z_high 1 10 16

Predstavljanje nesavršenog znanja Neka je na ulazu u sustav izrazite vrijednosti: x=0. 0, y=3. 2 Sustav mora odrediti izrazitu vrijednost z. Postupak: 1. Izračunaj konjunkciju AKO strana svakog pravila (oznaka 1, 2, 3, 4). ( se računa operacijom min, t. j. za svaku lingvističku varijablu izračuna se vrijednost karakteristične funkcije za izraziti ulaz i odabere najmanja vrijednost između svih konjunkcijskih članova u pojedinom pravili) 1: U prvom pravilu x_low za x=0. 0 slijedi =1. 0, a y_low za y=3. 2 slijedi =0. 68. Minimum je dakako 0. 68, te je 1=0. 68. Analogno za ostala pravila. 1 = 0. 68 2 = 0. 32 3 = 0 4 = 0 17

Predstavljanje nesavršenog znanja Nakon određivanja konjunkcija, postupak se nastavlja na dva moguća načina (2. 1. i 2. 2. ). 2. 1. 1. Zaključivanje MIN_MAX postupkom: utječe na TADA stranu odgovarajućeg pravila tako da reže njegovu karakterističnu funkciju, ovdje (z). Rezultat su izmijenjene karakteristične funkcije lingvističkih varijabli TADA strane svakog pravila. rule 1(z) = z/10, ako z 6. 8 0. 68, ako z 6. 8 rule 2(z) = 0. 32, ako z 6. 8 1 - z / 10, ako z 6. 8 rule 3(z) = 0. 0 8. 4 1. 0 fuzzy(z) 0. 68 0. 32 R 1 R 2 rule 4(z) = 0. 0 R 3, R 4 3. 2 6. 8 10 18

Predstavljanje nesavršenog znanja 2. 1. 2. Izvede se kompozicija svih pravila MAX postupkom Kompozicija se izvodi povlačenjem po maksimumima (označeno točkasto na prethodnoj slici). Slijedi neizraziti zaključak temeljem svih pravila: fuzzy(z) = 0. 32, z/10, 0. 68, ako ako z 3. 2 z 6. 8 2. 1. 3. Odredi se izrazita vrijednost zaključka (engl. defuzzification) postupkom AVG_OF_MAXIMA (srednja vrijednost maksimuma). Izrazita vrijednost zaključka: z = 8. 4 19

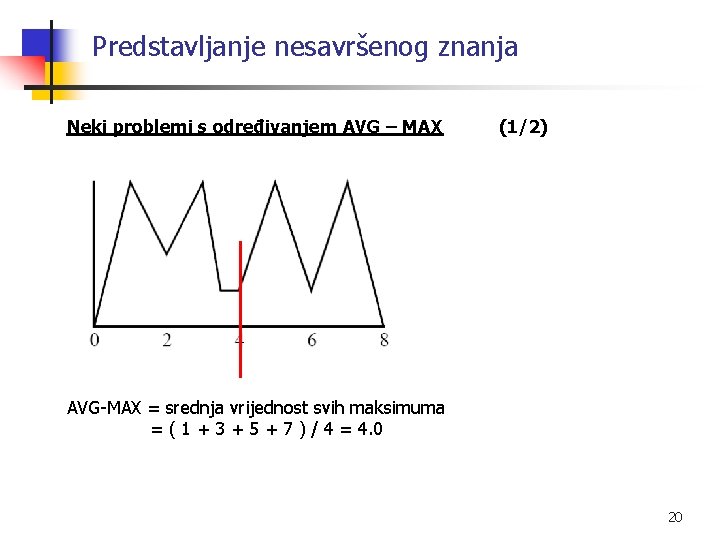
Predstavljanje nesavršenog znanja Neki problemi s određivanjem AVG – MAX (1/2) AVG-MAX = srednja vrijednost svih maksimuma = ( 1 + 3 + 5 + 7 ) / 4 = 4. 0 20

Predstavljanje nesavršenog znanja Neki problemi s određivanjem AVG – MAX (2/2) Raniji postupak: ( 1 + 2 + 3 + 4 + 6 + 8) / 6 = 4. 0 Bolje težinski: Zbrajamo umnoške sredine i širine intervala maksimuma. Dijelimo sa sumom širina intervala. Prvi interval: sredina maksimuma u točki 1. 5, širina intervala 1. 0. Analogni postupak za ostale rezultira u: (1. 5 x 1 + 3 x 0 + 5 x 2 + 8 x 0) / (1 + 0 + 2 + 0) = 3. 833 21

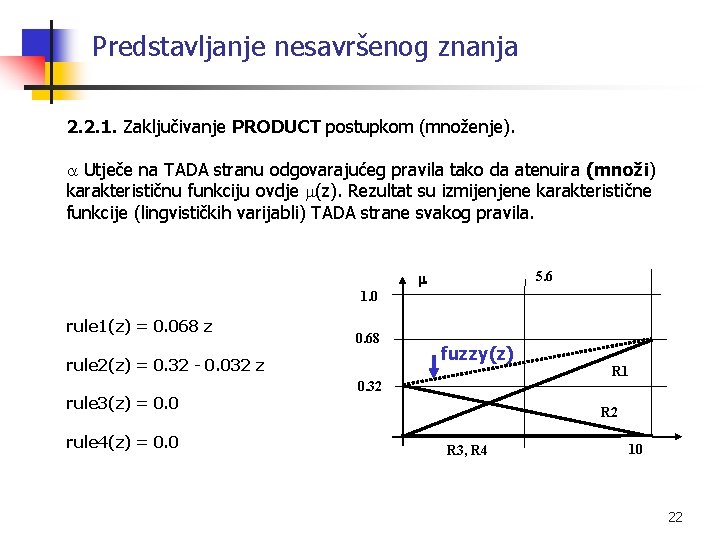
Predstavljanje nesavršenog znanja 2. 2. 1. Zaključivanje PRODUCT postupkom (množenje). Utječe na TADA stranu odgovarajućeg pravila tako da atenuira (množi) karakterističnu funkciju ovdje (z). Rezultat su izmijenjene karakteristične funkcije (lingvističkih varijabli) TADA strane svakog pravila. 5. 6 1. 0 rule 1(z) = 0. 068 z 0. 68 rule 2(z) = 0. 32 - 0. 032 z rule 3(z) = 0. 0 rule 4(z) = 0. 0 fuzzy(z) R 1 0. 32 R 3, R 4 10 22

Predstavljanje nesavršenog znanja 2. 2. 2. Izvede se kompozicija svih pravila SUMIRANJEM Iz kompozicije sumiranjem svih karakterističnih funkcija slijedi neizraziti zaključak temeljem svih pravila (označeno crtkano na prethodnoj slici). Može se dogoditi da suma karakterističnih funkcija daje vrijednosti > 1. U tom slučaju suma se mora skalirati prema dolje na maks 1. fuzzy(z) = 0. 32 + 0. 036 z 2. 2. 3. Odredi se izrazita vrijednost zaključka (engl. defuzzification) postupkom određivanja težišta (engl. centroid), t. j. podijeli se moment funkcije površinom ispod nje. moment f(w) = w f(w) dw, od 0 do 10 = = (0. 16 · 10 + 0. 012 · 10) = (16 + 12) = 28 površina f(w) = f(w) dw, od 0 do 10 = = (0. 32 · 10 + 0. 018 · 100) = (3. 2 + 1. 8) = 5. 0 Težište je 5. 6, pa je izrazita vrijednost zaključka z = 5. 6 23

Predstavljanje nesavršenog znanja Sustavi temeljeni na neizrazitim pravilima - sažetak • • Podudaranje AKO strana pravila s činjenicama: • ako su činjenice izrazite, a konjunkcijski članovi neizraziti, očitaju se vrijednosti karakterističnih funkcija svakog člana. • Izračun ukupne AKO strane ( ) izvodi se operacijom MIN. djeluje na neizrazitu TADA stranu (danu karakterističnom funkcijom) na način da: • Reže odgovarajuću karakterističnu funkciju TADA strane svakog pravila, te: • • • Izvede se kompozicija svih izmijenjenih karakterističnih funkcija TADA strana pravila MAX postupkom. Slijedi neizraziti zaključak. Izraziti zaključak izvede se AVG_OF_MAX postupkom. ili na način da: • Množi odgovarajuću karakterističnu funkciju TADA strane svakog pravila, te: • • • Izvede se kompozicija svih izmijenjenih karakterističnih funkcija TADA strana pravila sumiranjem. Slijedi neizraziti zaključak. Izraziti zaključak izvede se izračunom težišta. To je preporučena metoda u primjenama automatskog upravljanja. 24

Predstavljanje nesavršenog znanja Sustavi temeljeni na neizrazitim pravilima Do sada je promatrano: Činjenice izrazite, konjunkcijski dijelovi AKO strane pravila neizraziti, TADA strane pravila neizrazite. Moguće su sve kombinacije: 1. Sve činjenice izrazite, svi konjunkcijski dijelovi AKO strane izraziti: Mora postojati potpuno slaganje svih parova činjenica-konjunkcijski dio AKO strane, t. j. =1. Nakon toga: n n ako je TADA strana izrazita, slijedi klasičan ekspertni sustav s pravilima (CLIPS). ako je TADA strana neizrazita, karakteristična funkcija te strane je neizmijenjena ( =1). Kompozicija svih TADA strana i izračun izrazitog zaključka slijedi postupak kao što je pokazano ranije. 25

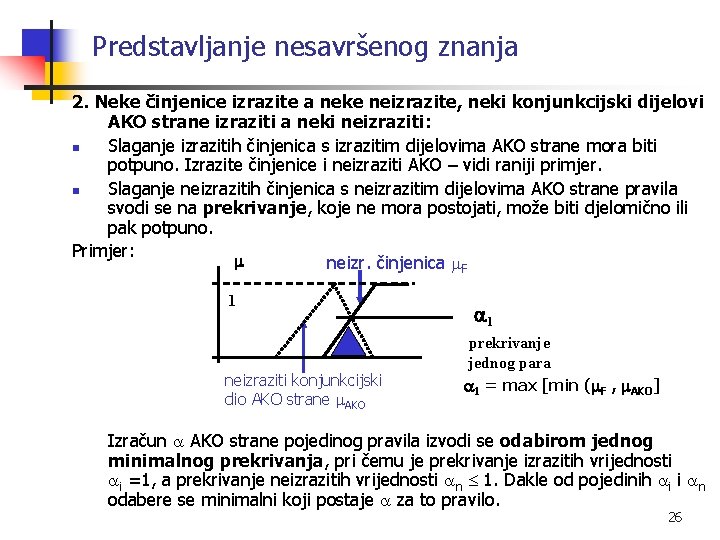
Predstavljanje nesavršenog znanja 2. Neke činjenice izrazite a neke neizrazite, neki konjunkcijski dijelovi AKO strane izraziti a neki neizraziti: n Slaganje izrazitih činjenica s izrazitim dijelovima AKO strane mora biti potpuno. Izrazite činjenice i neizraziti AKO – vidi raniji primjer. n Slaganje neizrazitih činjenica s neizrazitim dijelovima AKO strane pravila svodi se na prekrivanje, koje ne mora postojati, može biti djelomično ili pak potpuno. Primjer: neizr. činjenica F 1 neizraziti konjunkcijski dio AKO strane AKO 1 prekrivanje jednog para 1 = max [min ( F , AKO] Izračun AKO strane pojedinog pravila izvodi se odabirom jednog minimalnog prekrivanja, pri čemu je prekrivanje izrazitih vrijednosti i =1, a prekrivanje neizrazitih vrijednosti n 1. Dakle od pojedinih i i n odabere se minimalni koji postaje za to pravilo. 26

Predstavljanje nesavršenog znanja n n n Zaključujemo da u slučaju kada su neke činjenice izrazite a neke neizrazite, i neki konjunkcijski dijelovi AKO strane izraziti a neki neizraziti generira se kao minimalno prekrivanje odgovarajućih parova činjenica i konjunkcijskih dijelova AKO strane. Vrijednost je u intervalu [0, 1]. Ako je TADA strana pravila izrazita, pravilo se aktivira ali se TADA strana ne mijenja. Ako je TADA strana pravila neizrazita, reže ili množi TADA stranu. Zaključivanje temeljem svih pravila slijedi ranije pokazan postupak. Nedostatak pokazanog postupka zaključivanja u sustavu temeljenom na neizrazitoj logici: n Pretraživanje prekrivajućih parova činjenica i dijelova AKO strana pravila je dugotrajno. n I najmanje prekrivanje na AKO strani stavlja pojedino pravilo u skup za donošenje zaključka. n U donošenju zaključka (AVG_OF_MAX ilii TEŽIŠTE) sudjeluje veliki broj pravila što rezultira u sporom izvođenju. 27

Predstavljanje nesavršenog znanja Poboljšanje efikasnosti sustava zasnovanog na neizrazitoj logici Faktori izvjesnosti (CF) - (engl, certainty factor) Ideja: n Činjenicama i pravilima pridružiti težinske faktore CFi koji opisuju značaj toga entiteta u sustavu. n Pri izračunu prekrivanja parova činjenica i AKO dijelova pravila odrediti CFAKO za cijeli AKO dio pravila. n Temeljem izvornog CF pravila i izračunatog CFAKO za AKO stranu pravila odrediti novi faktor izvjesnosti CFC svakog pravila. n Ako je novi faktor izvjesnosti pravila manji od unaprijed postavljenog praga, to pravilo treba isključiti iz skupa za donošenje zaključka. 28

Predstavljanje nesavršenog znanja Određivanje izvornih faktora izvjesnosti Činjenice: pridruživanje CF svakoj činjenici je sasvim heuristički (npr. točnost mjerenja neke veličine, statistički iz povijesti itd. ). Pravila: Najčešće koristimo pojednostavljene uvjetne vjerojatnosti kao faktore izvjesnosti. AKO: E, TADA: H, P(H | E) (ovdje samo jedan član na AKO strani) gdje je P(H | E) uvjetna vjerojatnost da će se dogoditi H (hipoteza) ako se dogodio E (evidencija). Uvjetna vjerojatnost P(H | E) može semantički preuzeti ulogu faktora izvjesnosti CF pravila. Primjer iz medicine: Liječnik zna (iz svoje statistike) da je apriorna vjerojatnost meningitisa P(M), apriorna vjerojatnost ukrućenog vrata P(V), te vjerojatnost ukrućenog vrata kod dijagnosticiranog meningitisa P(V | M). Kolika je vjerojatnost meningitisa ako se pojavi pacijent s ukrućenim vratom ? P(M | V) je vjer. hipoteze uz evidenciju t. j. P(H | E), odnosno faktor izvjesnosti CF. P(M | V) = P(V | M) · P(M) / P(V) uz uporabu Bayesovog pravila 29

Predstavljanje nesavršenog znanja Određivanje izvornih faktora izvjesnosti Pravilo s više dijelova na AKO strani: AKO: E 1, E 2, . . . , Em, TADA: H, P(H | E 1, E 2, . . . , Em) Bayesovo pravilo daje: P(E 1, E 2, . . . , Em | Hk) P(H | E 1, E 2, . . . , Em) = ------------------P(E 1, E 2, . . . , Em) m istodobnih Em (simptoma) zahtijeva 2 m (svi podskupovi) apriornih vjerojatnosti. Eksponencijalna složenost nedopustiva. Redukcija složenosti: Ei su međusobno nezavisni (vrlo jako pojednostavljenje). P(E 1, E 2, . . . , Em | Hk) = P(E 1 | Hk) · P(E 2 | Hk) · … · P(Em | Hk) P(E 1, E 2, . . . , Em) = P(E 1) · P(E 2) · … · P(Em) P(E 1 | Hk) P(H | E 1, E 2, . . . , Em) = P(Hk) ------P(E 1) P(E 2 | Hk) P(Em | Hk) ------. . . ------P(E 2) P(Em) 30

Predstavljanje nesavršenog znanja Računanje s faktorima izvjesnosti CF n n Izvorni faktori izvjesnosti činjenica CFi dobiveni heuristički. Izvorni faktori izvjesnosti pravila CFR dobiveni pojednostavljenom uvjetnom vjerojatnosti. 1. Određivanje CF s izrazitim vrijednostima Činjenice: Pravilo: izrazite s faktorima izvjesnosti CF 1. . . CFn AKO strane izrazite, TADA strana izrazita ili ne, faktor izvjesnosti pravila CFR. Novi faktor izvjesnosti pravila: CFC = CFR min[CF 1 , . . . , CFn] Odabere se minimalni CF temeljem slaganja parova činjenica s AKO dijelovima u pravilu. Dobiveni minimalni CF množi izvorni CF R pravila. Slijedi faktor izvjesnosti zaključka (TADA strane pravila) CF C. 31

Predstavljanje nesavršenog znanja 2. Određivanje CF s neizrazitim vrijednostima Moramo promotriti zasebno svaki par prekrivanja (jedna neizrazita činjenica i jedan neizraziti dio u AKO strani pravila). Činjenica: Pravilo: neizrazita, faktor izvjesnosti CF~1 (npr. 0. 8) AKO strana neizrazita, TADA strana izrazita ili ne, faktor izvjesnosti pravila CF~R (npr. 0. 7) Novi faktor izvjesnosti pravila: CFC = (CF~ · S 1) · CF~R gdje je S 1 = mjera sličnosti činjenice i AKO dijela s kojim se činjenica prekriva. Ako postoji prekrivanje više parova činjenica i dijelova AKO strane, u izračunu se uzima minimalni umnožak faktora izvjesnosti činjenice i odgovarajuće sličnosti s AKO dijelom pravila. Taj se umnožak dalje množi s izvornim faktorom izvjesnosti pravila CF~R. CFC = {min[(CF 1· S 1), (CF 2· S 2), … (CFm· Sm)] · CF~R } 32

Predstavljanje nesavršenog znanja Izračunavanje mjere sličnost (Cayrol, Farency, Prade 1982) S = P(R | F) ako N(R | F) > 0. 5 = [N(R | F) + 0. 5] P(R | F) inače gdje je: R = karakt. funkcija jednog konjunkcijskog dijela AKO strane F = karakt. funkcija jedne činjenice P(R | F) = max [ min ( R, F )] - mjera mogućnosti (engl. possibility) N(R | F) = 1 - P(R' | F ) - mjera nužnosti (engl. necessity) R’ je komplement, t. j. R' = 1 - R Primjer: P(R | F) = max min = 0. 8 F R prekrivanje (min) pa vrh (max) 33

Predstavljanje nesavršenog znanja Izračunavanje mjere sličnost (Cayrol, Farency, Prade 1982) Sad računamo P(R’ | F): F 1 - R P(R’ | F) = max min = 0. 667 N ( R | F) = 1 - P(R' | F) = 1 - 0. 667 = 0. 333 Što je < 0. 5 , te je sličnost: S = [ N(R | F) + 0. 5 ] P( R | F) = [ 0. 333 + 0. 5 ] 0. 8 = 0. 667 Prema tome je novi faktor izvjesnosti pravila (pod pretpostavkom da postoji samo jedan par činenica – AKO član): CFC = (CFF S ) · CFR = 0. 8 x 0. 667 x 0. 7 = 0. 3733 Može se postaviti prag okidanja pravila > 0. 4, te ovo pravilo neće sudjelovati u zaključku. Uobičajeno (heuristički): CFC > 0. 25 34

Predstavljanje nesavršenog znanja Dodatni postupci za izračun faktora izvjesnosti Upis nove činjenice kao rezultat zaključivanja Npr. : Činjenica: F 1 , CFF 1 =0. 9 Pravilo: AKO F 1, TADA (F 2 uz CFF 2 = 0. 7) , CFR = 0. 8 Pravilo se aktivira (F 1 AKO F 1) i nova činjenica F 2 upisuje se u skup činjenica, ali sa promijenjenim faktorom izvjesnosti CF F 2 : CFF 2 = 0. 9 x 0. 7 x 0. 8 = 0. 504 35

Predstavljanje nesavršenog znanja Dodatni postupci za izračun faktora izvjesnosti Višestruki doprinos jednoj hipotezi Pravilo može svojim zaključkom upisati činjenicu Fn (uz faktor izvjesnosti CFFn ) , koja već postoji u skupu činjenica kao F (uz faktor izvjesnosti (CFF ). (Vidi raniji primjer uz pretpostavku da je F 1 = F 2). Obnovljena (ista) činjenica dobiva novifaktor izvjesnosti: CF = max [ CFFn , CFF ] n n Ako su nova i stara vrijednost činjenice izrazite: obnovljena izrazita vrijednost ostaje neizmijenjena. Mijenja se samo faktor izvjesnosti (max). Ako su nova i stara vrijednost činjenica neizrazite: obnovljena vrijednost je unija dviju karakterističnih funkcija (karakteristične funkcije iste neizrazite činjenice mogu se razlikovati zbog npr. primjene različitog modifikatora lingvističke varijable – činjenice). 36

Predstavljanje nesavršenog znanja Zaključci o rukovanju s neizrazitim (nejasnim) znanjem n n n n Primjena neizrazite logike u oblikovanju ekspertnih sustava ima problematičan izbor operatora (npr. inženjerska implikacija, sličnost S, prag okidanja, računanje faktora izvjesnosti). Rukovanje s faktorima izvjesnosti (težinskim faktorima činjenica i pravila) nije utemeljeno na matematički potvrđenoj teoriji. Činjenicama se faktori izvjesnosti pridjeljuju heuristički. Pravilima se faktori izvjesnosti pridjeljuju preko pojednostavljene uvjetne vjerojatnosti. Ulančavanjem konjunkcija u AKO strani pravila izvodi se skupni faktor izvjesnosti AKO strane pravila operacijom MIN. Izmijenjeni težinski faktor aktiviranog pravila izvodi se operacijom PRODUKT. Ako se aktivacijom pravila upisuje nova činjenica, njen izvorni faktor izvjesnosti se modificira tako da se množi sa skupnim faktorom AKO strane i s faktorom izvjesnosti pravila. Za višestruki upis iste činjenice (višestruka potvrda hipoteze) obnovljeni faktor izvjesnosti izvodi se operacijom MAX (unija). 37