Predicting Energy Expenditure ACSM Metabolic Equations Why useful

Predicting Energy Expenditure ACSM Metabolic Equations

Why useful? Exercise prescription ACSM certification exam

Basic Algebra Review Solve for Y when you are given X E. g. Y = 800 + (3. 2 x) Solve for Y when x = 47

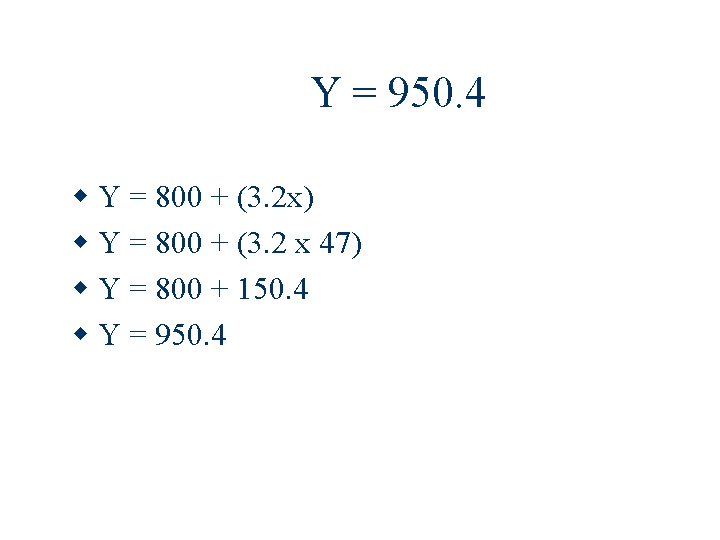
Y = 950. 4 Y = 800 + (3. 2 x) Y = 800 + (3. 2 x 47) Y = 800 + 150. 4 Y = 950. 4

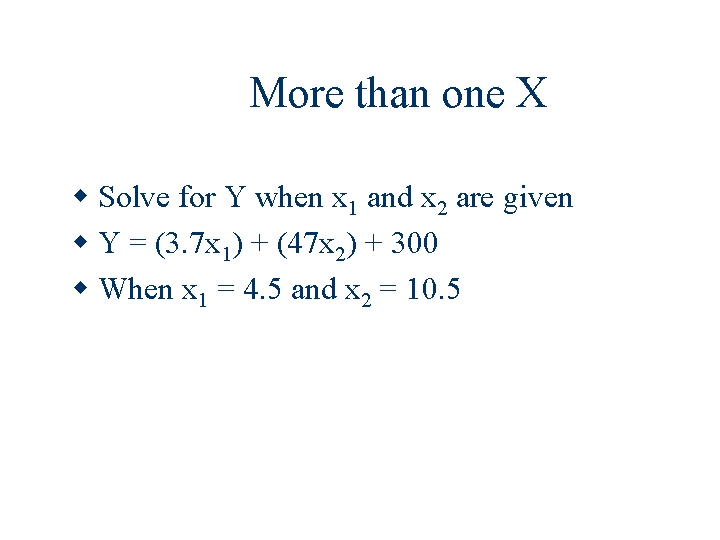
More than one X Solve for Y when x 1 and x 2 are given Y = (3. 7 x 1) + (47 x 2) + 300 When x 1 = 4. 5 and x 2 = 10. 5

Y = 810. 15 Y = (3. 7 x 1) + (47 x 2) + 300 Y = (3. 7 x 4. 5) + (47 x 10. 5) + 300 Y = 16. 65 + 493. 5 + 300 Y = 810. 15

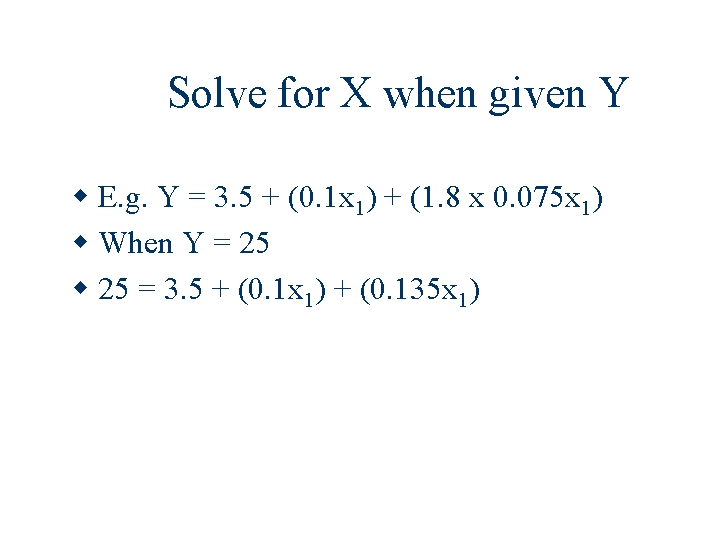
Solve for X when given Y E. g. Y = 3. 5 + (0. 1 x 1) + (1. 8 x 0. 075 x 1) When Y = 25 = 3. 5 + (0. 1 x 1) + (0. 135 x 1)

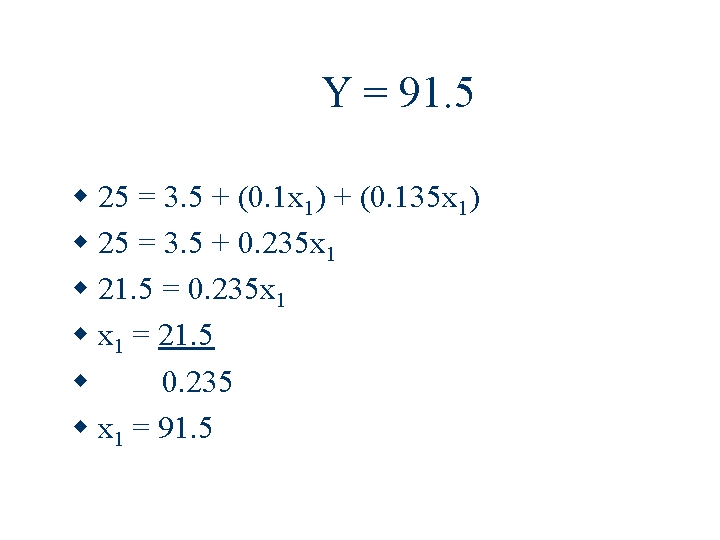
Y = 91. 5 25 = 3. 5 + (0. 1 x 1) + (0. 135 x 1) 25 = 3. 5 + 0. 235 x 1 21. 5 = 0. 235 x 1 = 21. 5 0. 235 x 1 = 91. 5

Basic Energy Expenditure Principles Mass – def. – the weight of an object at rest Force – def. – the weight of an object in motion

Work – def. – the application of force through a distance Work = force x distance E. g. A 75 kg man walks 10 meters. He has done 750 kgm of work.

Power – def. – work divided by time Power = w or f x d t t

2 Types of Power Mechanical power Weight lifting Metabolic power E. g. aerobic power or oxygen uptake (VO 2) VO 2 units – ml. kg. min.

If Power is f x d, then… t If a person pedals a Monark cycle ergometer with 1. 5 kg of resistance on the flywheel and is pedaling at 50 rpm, then that person has a power output of 450 kg. m. min. Note: Monark cycle ergometers have a flywheel travel distance of 6 meters per revolution.

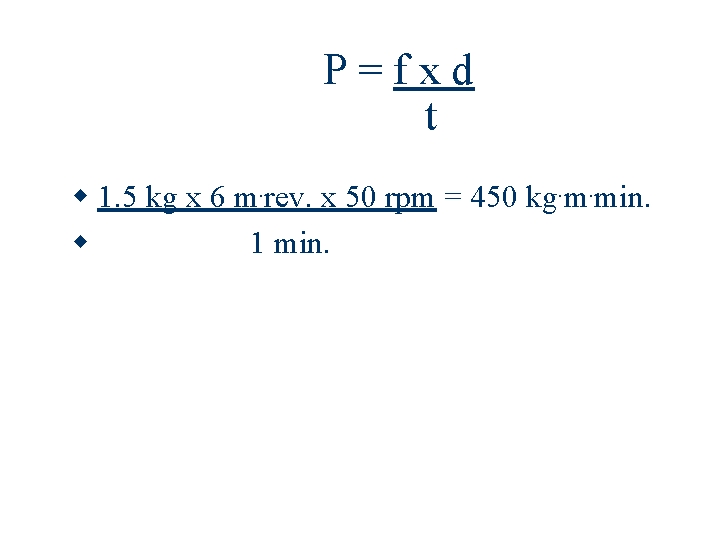
P=fxd t 1. 5 kg x 6 m. rev. x 50 rpm = 450 kg. m. min. 1 min.

Energy – def. – capability to produce force, perform work, or generate power. Units: Energy expenditure – kcal Cycle workrates – kg. m. min. Aerobic power – ml. kg. min.

Aerobic Power (VO 2) Absolute and relative energy expenditure Absolute VO 2 – total amount of O 2 used (L. min. or ml. min. ) 1 L of O 2 burns 5 kcal

Relative VO 2 = total O 2 body weight E. g. – Man weighs 110 kg and has VO 2 of 3. 0 L. min. Boy weighs 50 kg and has VO 2 of 3. 0 L. min. Who has higher relative aerobic power?

Man – 110 kg = 27. 3 3000 ml . . ml kg min Boy – 50 kg = 54. 5 ml. kg. min. 3000 ml Therefore, the boy has higher relative aerobic power.

METS MET – def. – 3. 5 ml. kg. min. of aerobic power How many METS does a woman with 45 ml. kg. min. have?

Answer – 12. 9 Mets 45/3. 5 = 12. 857 Mets

Example of Energy Expenditure Calculation John walks at 2. 5 mph up a 2% grade on a treadmill. He weighs 75 kg. How many kcal is he expending? Which equation? What VO 2 units will answer give? Which VO 2 units do you need to calculate kcal?

Step 1 – Determine VO 2 using the walking equation Convert speed from mph to m. min. 26. 8 x 2. 5 = 67 m. min. VO 2 = (speed x 0. 1) + (speed x grade x 1. 8) + 3. 5 = (67 x 0. 1) + (67 x 0. 02 x 1. 8) + 3. 5 = 6. 7 + 2. 4 + 3. 5 VO 2 = 12. 6 ml. kg. min.

Step 2 – Convert units to L. min. Ml. min. = ml. kg. min. x body weight (kg) = 12. 6 x 75 = 945 ml. min. Convert ml. min. to L. min. = 945/1000 = 0. 945 L. min.

. L min. Step 3 – Convert. kcal min. Kcal. min. = L. min. x 5 = 0. 945 x 5 = 4. 7 kcal. min. into

How many minutes would it take for John to lose a pound of fat? 1 pound of fat = 3500 kcal. 3500/4. 7 kcal. min. = 744. 7 min.

ACSM Walking Equation VO 2 = horizontal component + vertical component + resting component = [speed (m. min. ) x 0. 1] + [grade x speed x 1. 8] + 3. 5

Problem: What is Sue’s VO 2 if she walks at 3 mph up a 7. 5% grade on the treadmill?

Answer: 22. 4 ml. kg. min. Convert speed into m. min. 26. 8 x 3 = 80. 4 VO 2 = (80. 4 x 0. 1) + (0. 075 x 80. 4 x 1. 8) + 3. 5 = 8. 04 + 10. 85 + 3. 5 = 22. 4 ml. kg. min.

What is the VO 2 expressed in Mets? 1 Met = 3. 5 ml. kg. min. 22. 4 ml. kg. min. = 22. 4/3. 5 = 6. 4 Mets

Problem: At what speed would Jim need to walk at 7. 5% grade on the treadmill to use 20 ml. kg. min. of O 2? 20 ml. kg. min. = (0. 1 x) + [(0. 075 x) x 1. 8] + 3. 5

Answer: 2. 6 mph 20 = (0. 1 x) + [(0. 075 x) x 1. 8] + 3. 5 16. 5 = 0. 1 x + 0. 135 x 16. 5 = 0. 235 x X = 16. 5 = 70. 2 m. min. 0. 235 70. 2/26. 8 = 2. 6 mph

ACSM Running Equation VO 2 = horizontal component + vertical component + resting component VO 2 = [speed (m. min. ) x 0. 2] + [grade x speed (m. min. ) x 0. 9] + 3. 5

Problem: What is Frank’s VO 2 if he runs at 6. 7 mph up a 10% grade on the treadmill? Convert speed into m. min. 26. 8 x 6. 7 = 179. 6 m. min. VO 2 = (179. 6 x 0. 2) + (. 10 x 179. 6 x 0. 9) + 3. 5 = 35. 9 + 16. 2 + 3. 5 = 55. 6 ml. kg. min.

Problem: What is the VO 2 for the previous example if the grade were increased to 12%? Only change is the vertical component; thus you can use the horizontal and resting component values from previous example. Horizontal component = 35. 9 Resting component = 3. 5 Vertical component = (. 12 x 179. 6 x 0. 9) = 19. 4 VO 2 = 35. 9 + 19. 4 + 3. 5 = 58. 8 ml. kg. min.

Leg Cycling Power Output = resistance x rpm x m. rev. E. g. 3 kg x 60 rpm x 6 m/rev. = 1080 kgm. min. 1 Watt = 6 kgm. min. 1080/6 = 180 watts

ACSM Leg Cycling Equation VO 2 = resistive component + resting component VO 2 = (power output x 2) + (3. 5 x body weight)

Problem: What is the VO 2 for a cyclist who pedals at a power output of 640 kgm. min. and who weighs 78 kg? VO 2 = (640 x 2) + (3. 5 x 78) = 1280 + 273 = 1553 ml. min. (absolute VO 2) 1553/78 = 19. 9 ml. kg. min. (relative VO 2)

ACSM Arm Cycling Equation VO 2 = (power output x 3) + (3. 5 x body weight) E. g. Pete arm cycles at a power output of 300 kgm. min. What is his VO 2 if he weighs 68 kg?

Answer: 16. 7 ml. kg. min. VO 2 = (300 x 3) + (3. 5 x 68) = 900 + 238 = 1138 ml. min. 1138/68 = 16. 7 ml. kg. min.

ACSM Stepping Equation VO 2 = horizontal component + vertical component VO 2 = [step rate (steps. min. ) x 0. 35] + [step height(m) x step rate x 1. 33 x 1. 8]

Convert step height from inches to meters Inches x 2. 54/100 E. g 12 inch step converts to: 12 x 2. 54/100 = 0. 3 m

Problem: Anne steps up and down at a rate of 24 steps per minute on a 16 inch bench. What is her VO 2? VO 2 = (24 x 0. 35) + [(16 x 2. 54/100) x 24 x 1. 33 x 1. 8] = 8. 4 + 22. 9 = 31. 4 ml. kg. min.

Problem: Marianne steps up and down a 6 inch bench at a step rate of 30 steps per minute. What is her VO 2? Don’t forget to convert step height to meters.

Answer: 21. 4 ml. kg. min. VO 2 = (30 x 0. 35) + [(6 x 2. 54/100) x 30 x 1. 33 x 1. 8] = 10. 5 + 10. 9 = 21. 4 ml. kg. min.