Precalculus Spiral Final exam preparation questions Algebra Graphing

Precalculus Spiral Final exam preparation questions Algebra Graphing Exponential Trigonometry Limits Stat/probability

Functions: find f(2) and f(-3) 1. ) 2. ) 3. )

Composition: find f(g(x)) 1. ) 2. ) 3. )

Operations: Subtract and multiply 1. ) 2. ) 3. )

Inverse: find f-1 1. ) 2. ) 3. )

Synthetic Division: divide 1. ) 2. ) 3. )

Parent graphs Draw the parent graphs for: Find Domain and Range for each graph

Transformations- describe them 1. ) 2. ) 3. )

Transformations- write equation 1. ) x 2, up 2, left 5, reflect over x-axis 2. ) absolute value, wider, right 2 3. ) square root, thinner, down 3

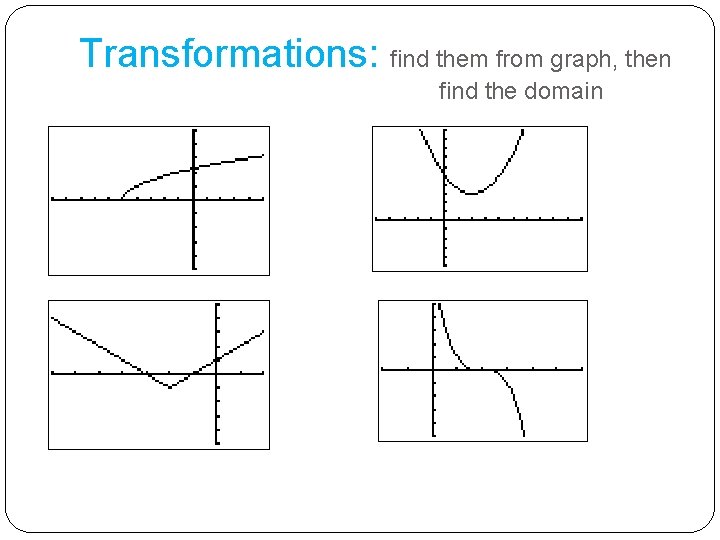
Transformations: find them from graph, then find the domain

Piecewise- find equation

Piecewise: Graph 1. ) 2. )

Domain- equation 1. ) 2. ) 3. )

Asymptotes- equation-VA &HA 1. ) 2. ) 3. )

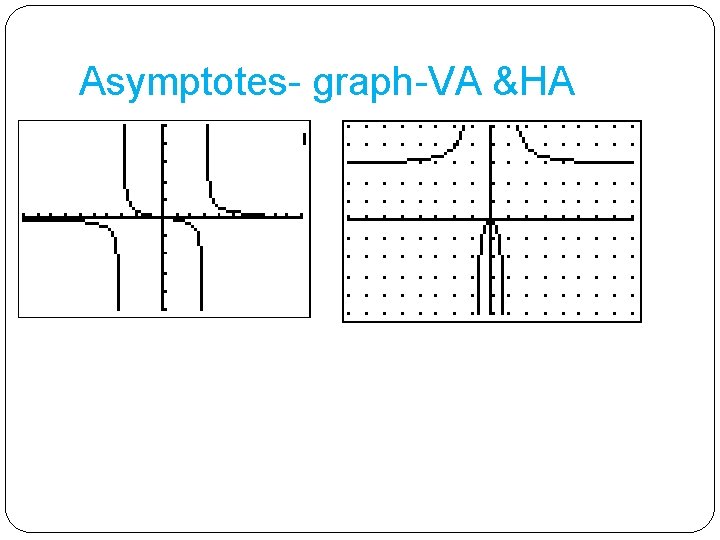
Asymptotes- graph-VA &HA

Roots-given roots- find equation, then graph 1. ) roots of 3 and -5, 2. ) roots of 2, -2, 0 3. ) roots of 2, 2 i, -2 i

Roots- roots from graph

Roots- Find roots from equation 1. ) 2. ) 3. )

Factor: trinomials and grouping 1. ) 2. ) 3. ) 4. )

Quadratic formula: 1. ) 2. ) 3. )

Graph 1. ) 2. ) 3. )

Solve- log and ln 1. ) 2. ) 3. ) 4. ) 5. ) 6. ) 7. ) 8. ) 9. )

Properties: expand 1. ) 2. ) 3. )

Properties: condense 1. ) 2. ) 3. )

Word problems- interpret variables Compounded Continuous Population

Word Problems 1. ) If $3000 is invested at 3. 5% interest compounded quarterly, what is the value after 10 years? 2. ) If $9500 is invested at 5% interest compounded daily, what is the value after 7 years? 3. ) Problem # 2 compounded continuously.

Word Problems (2) 4. ) You invest $2500 in an account that earns 7% interest compounded continuously. When will it double? 5. ) You invest $4550 in an account that earns 4. 5% interest compounded continuously. When will it be worth $10, 000? 6. ) You invest $1000 in an account that is compounded monthly. In 5 years it is worth $1475. Find the rate.

Word Problems (3) 7. ) The initial amount of bees is 50. They grow at a rate of 10% a day compounded continuously. Find the number of bees in 20 days. 8. ) The initial amount of a mass of radium is 4. 5 tons. It decays at a rate of -. 5% compounded continuously. Find the amount of radium in 100 years.

Convert To degrees: 1. ) 2. ) 3. ) To radians: 1. ) 225° 2. )-300° 3. ) 280°

Evaluate 1. ) 2. ) 3. ) 4. ) 5. ) 6. )

Given trig- find trig 1. ) If sinΘ = ¾ in quadrant II, find cotΘ 2. ) If cosΘ = -2/7 in quadrant III, find sinΘ 3. ) If cscΘ = 3 in quadrant I, find tanΘ

Graph- describe the graph 1. ) y = 3 cosΘ -2 2. ) y = cos(Θ-2) 3. ) y = 3 cos 2Θ -2 4. ) y = 3 cos(2Θ-2) 1. ) 2. ) 3. )

Simplify 1. ) 2. ) 3. )

Solve 1. ) 2. ) 3. ) 4. )

Law of Sines 1. ) 2. ) 3. )

Law of Cosines 1. )a = 3, b = 5, c = 7, angle A = ? 2. ) a = 4, b = 8, c = 11, angle B = ? 3. ) a = 2, b=7, c = 8, angle B = ?

Find the limit 1. ) 2. ) 3. )

Find the limit 1. ) 2. ) 3. )

Find the limit 1. ) 2. ) 3. ) 4. ) Do # 1 -3 as x approaches -∞

Find the Limit at x=3+, 3 - , 3

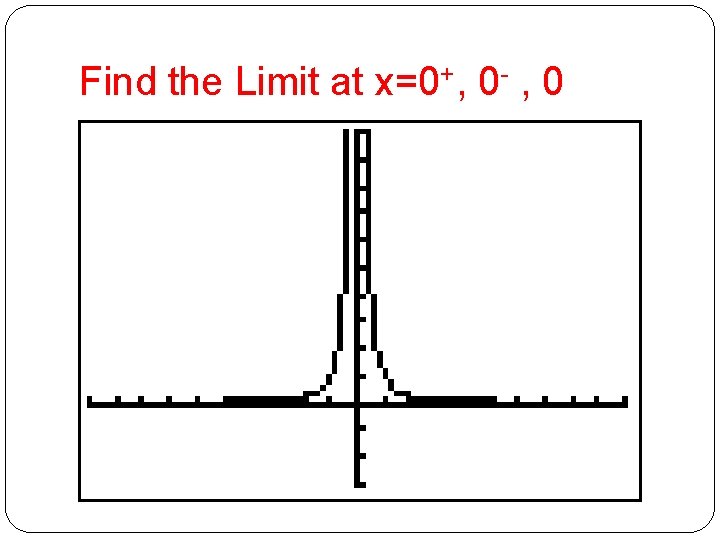
Find the Limit at x=0+, 0 - , 0

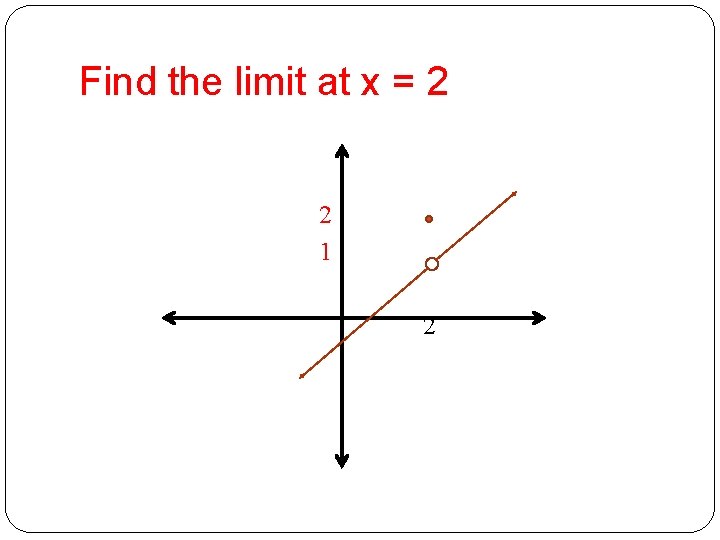
Find the limit at x = 2 2 1 2

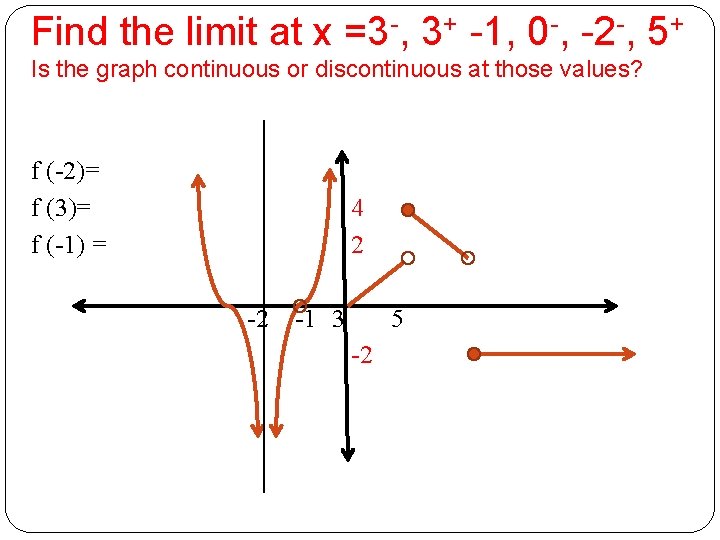
Find the limit at x =3 -, 3+ -1, 0 -, -2 -, 5+ Is the graph continuous or discontinuous at those values? f (-2)= f (3)= f (-1) = 4 2 -2 -1 3 5 -2

Where is the function discontinuous?

Continuity 1. ) Define f(2) in a way that extends to be continuous at x = 2. ) Define g(-4) in a way that extends to be continuous at x = -4. 3. ) Define h(1) in a way that extends continuous at x = 1. to be

Find the domain and range 1. ) 2. ) 3. ) 4. )

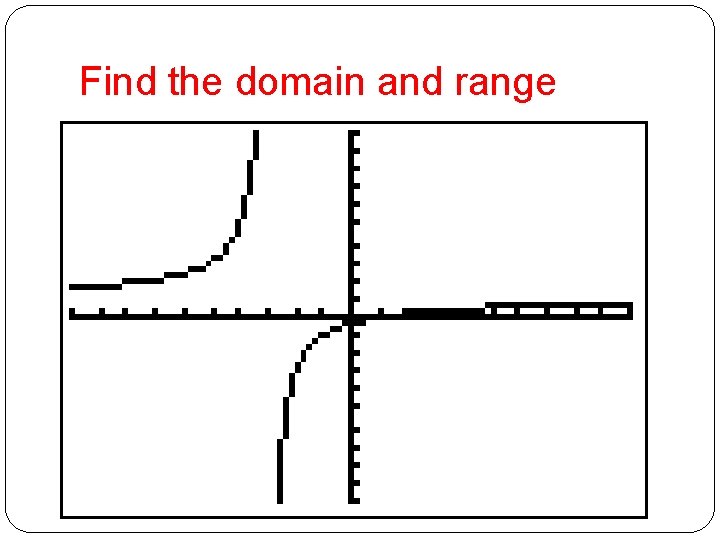
Find the domain and range

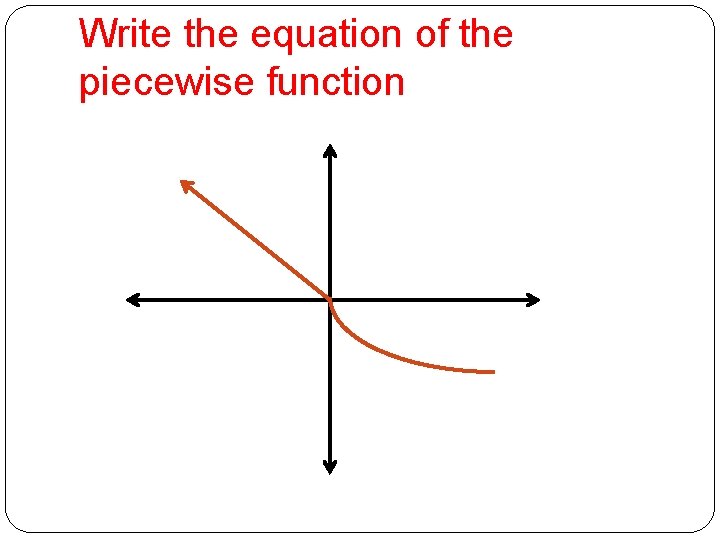
Write the equation of the piecewise function

Combinations 1. ) From a group of 10 men and 12 women, how many committees of 5 men and 5 women be formed? 2. ) From a group of 14 men and 8 women, how many committees of 5 men and 6 women be formed? 3. ) From a group of 12 men and 15 women, how many committees of 6 men and 4 women be formed?

Independent/dependent 1. ) A license plate has 7 characters in it where the first 4 are letters and the last 3 are numbers. If numbers and letters are allowed to be repeated, how many can be created? 2. ) A license plate has 7 characters in it where the first 4 are letters and the last 3 are numbers. If numbers and letters are not allowed to be repeated, how many can be created? 3. ) A license plate has 7 characters in it where the first 4 are numbers and the last 3 are letters. If numbers and

Replacement You have 3 green, 5 purple, and 6 red pens. Two are chosen at random without replacement. Write an expression describing: Red then green Red then red Purple then green Purple then purple Green then purple

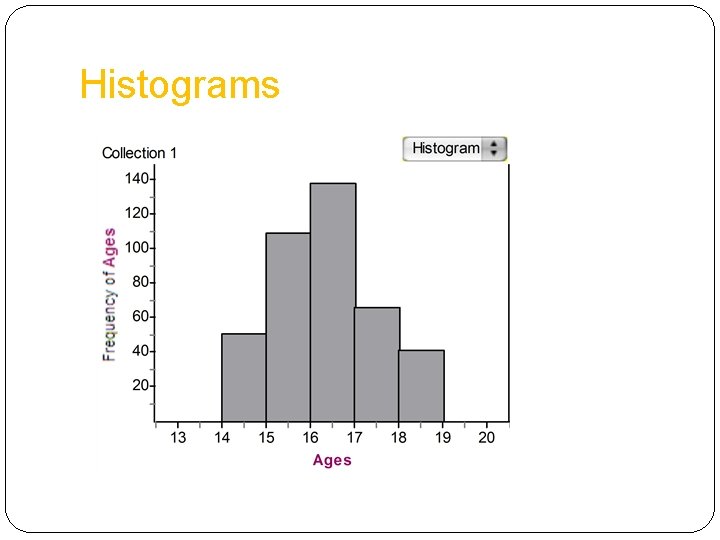
Histograms

Box and Whisker/IQR/Q 1 Q 2 Q 3