Precalculus Lesson 2 2 Polynomial Functions of Higher







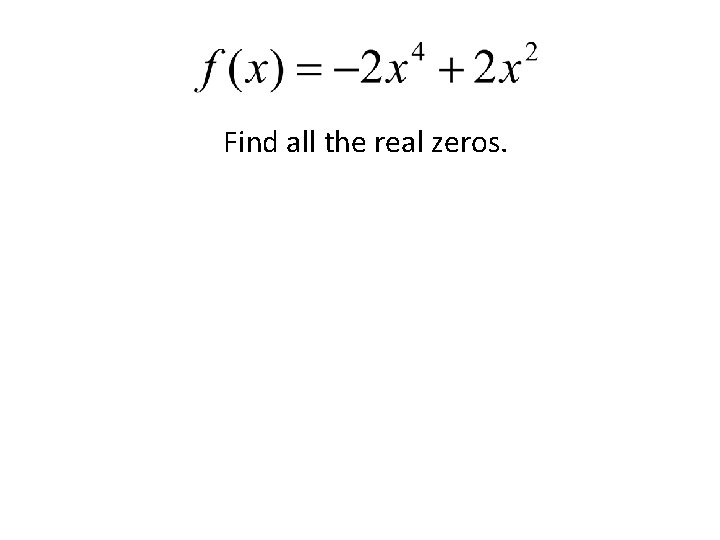

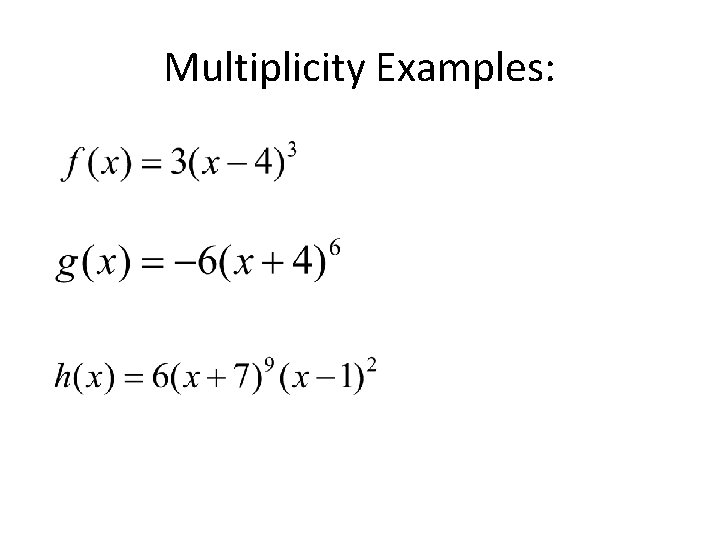





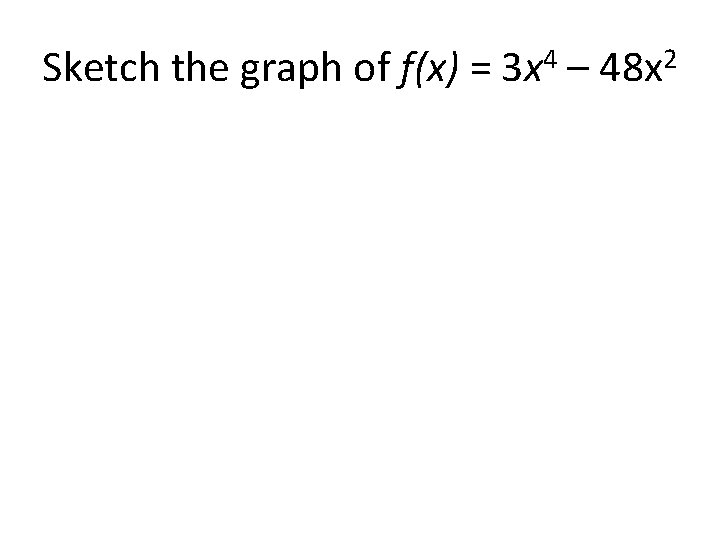
- Slides: 23

Precalculus Lesson 2. 2 Polynomial Functions of Higher Degree

Characteristics of Graphs of Polynomials • Polynomial functions are continuous. This means that the graphs of polynomial functions have no breaks, holes, or gaps. • The graphs of polynomial functions have only nice smooth turns and bends. There are no sharp turns, as in the graph of y = |x|.

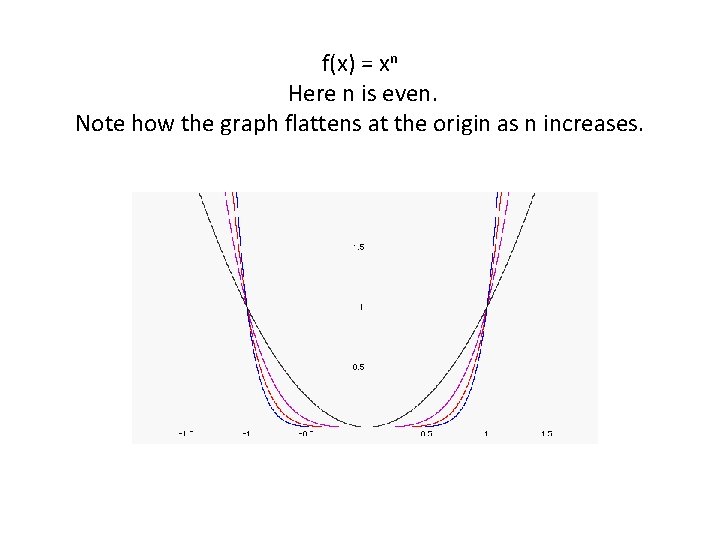
f(x) = xn Here n is even. Note how the graph flattens at the origin as n increases.

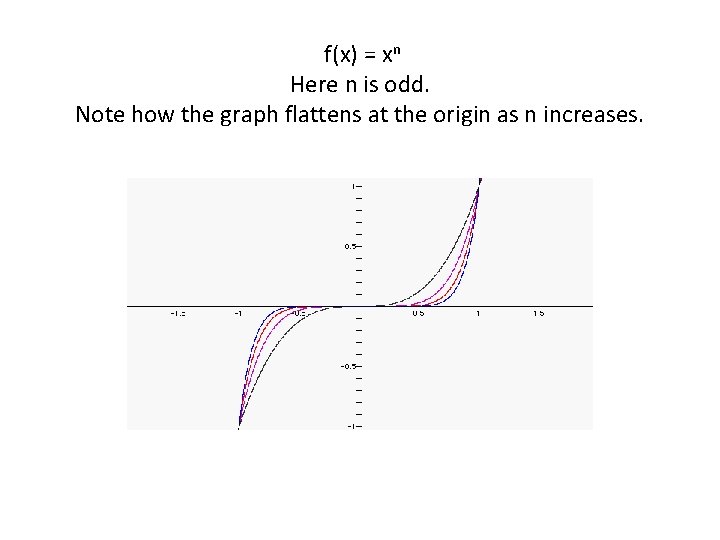
f(x) = xn Here n is odd. Note how the graph flattens at the origin as n increases.

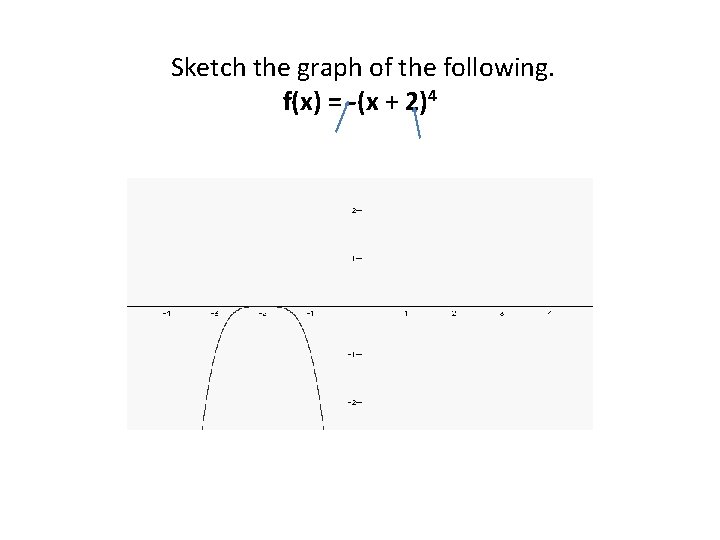
Sketch the graph of the following. f(x) = -(x + 2)4


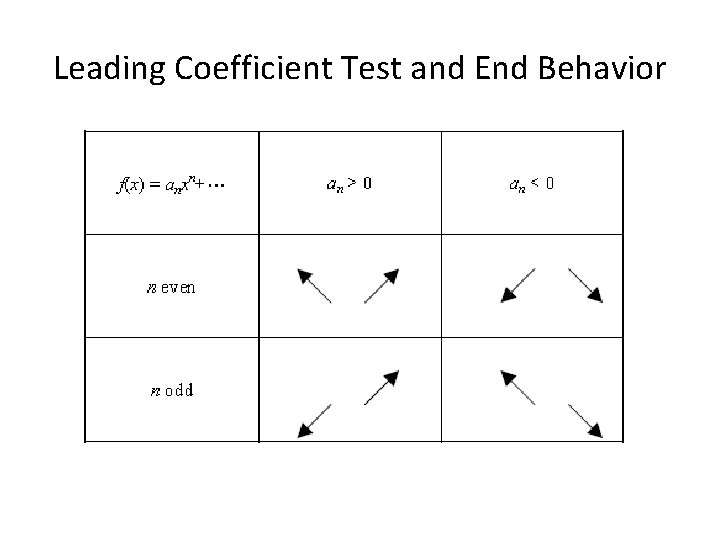
Leading Coefficient Test and End Behavior

Using the Leading Coefficient Test Describe the right-hand left-hand behavior of the graph of each function. Ask yourself 2 questions: 1. Is a positive or negative? 2. Is the exponent on the leading variable even or odd? a) f(x) = -x 4 + 7 x 3 – 14 x – 9 b) g(x) = 5 x 5 + 2 x 3 – 14 x 2 + 6

Zeros of Polynomial Functions For a polynomial function f of the degree n, the following statements are true: • The function f has at most n zeros. • The graph of f has at most n-1 relative maxima/minima. (Has at most n-1 turns)

Zeros of a Polynomial Function When f is a polynomial function and a is a real number: 1. x = a is a zero of f. 2. x = a is a solution of the equation f(x) = 0. 3. (x – a) is a factor of f(x). 4. (a, 0) is an x-intercept of the graph of f. These statements are all equivalent!

Find all the real zeros by factoring.

Find all the real zeros.
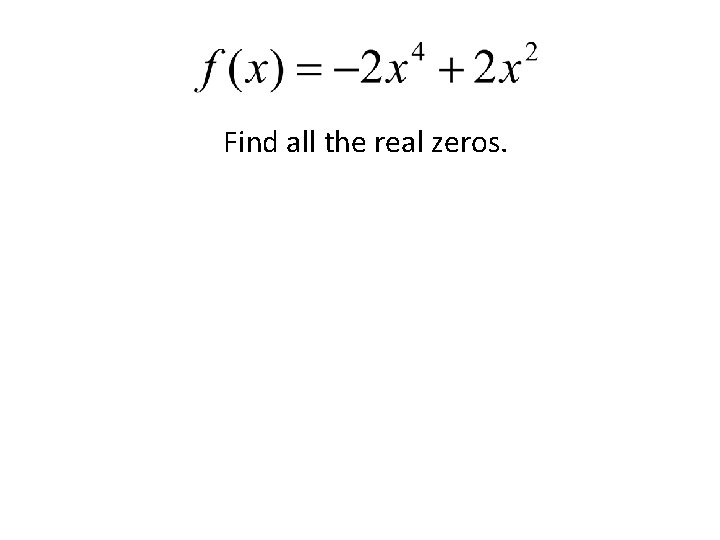
Find all the real zeros.

f(x) = 3 2 x –x – x+1 Find all the real zeros.

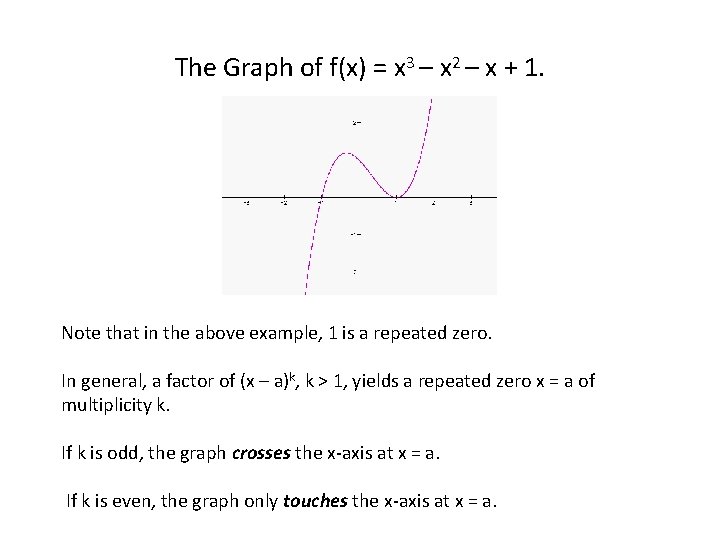
The Graph of f(x) = x 3 – x 2 – x + 1. Note that in the above example, 1 is a repeated zero. In general, a factor of (x – a)k, k > 1, yields a repeated zero x = a of multiplicity k. If k is odd, the graph crosses the x-axis at x = a. If k is even, the graph only touches the x-axis at x = a.
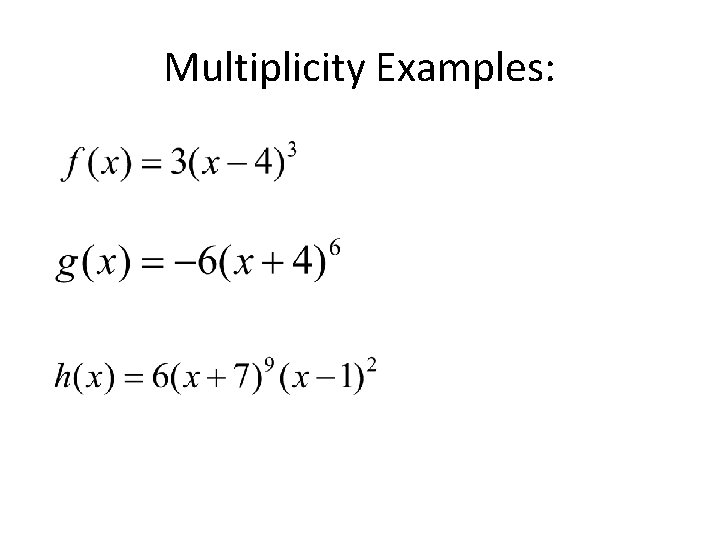
Multiplicity Examples:

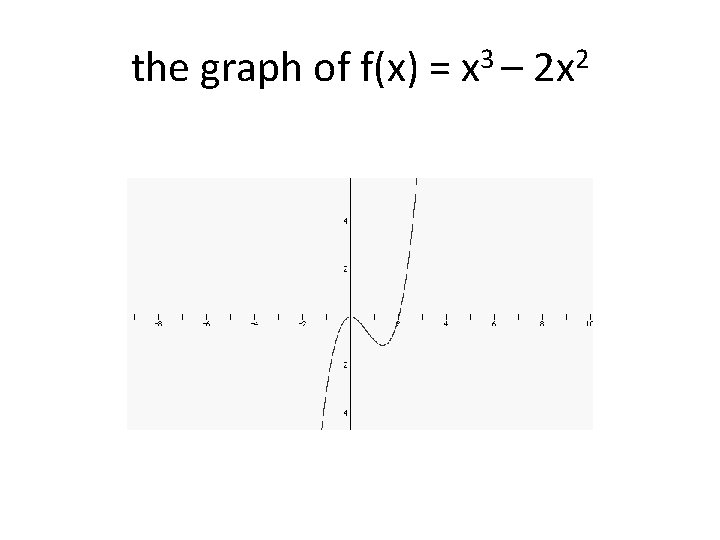
Some information you need to sketch the graph of f(x) = x 3 – 2 x 2 1. At most, how many real zeros does this function have? 2. At most, how many turns does this graph have? 3. Factor f(x) 4. What are the x-intercepts based on the factoring? 5. What do the multiplicity rules tell you about your xintercepts? 6. What does the leading coefficient test tell you about the end behavior of your graph?

the graph of f(x) = x 3 – 2 x 2

Finding a Polynomial Function with Given Zeros

Finding a Polynomial Function with Given Zeros

Finding a Polynomial Function with Given Zeros

Sketching the Graph of a Polynomial Function 1. Apply the leading coefficient test to determine the end behavior of the graph. 2. Determine the possible number of x-intercepts and turns. 3. Find the real zeros of the polynomial. 4. Plot a few additional points. (Make a table) 5. Draw the graph.
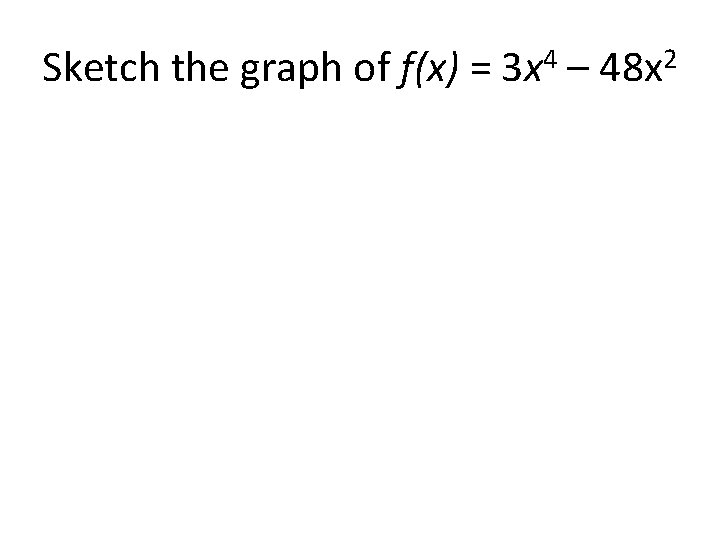
Sketch the graph of f(x) = 3 x 4 – 48 x 2