PreCalculus Honors 1 3 Graphs of Functions HW

Increasing and Decreasing Functions Determine the intervals on which each function is increasing, decreasing,

Increasing and Decreasing Functions The more you know about the graph of a function,

Even and Odd Functions • A function whose graph is symmetric with respect to

Even and Odd Functions A graph that is symmetric with respect to the x-axis

Even and Odd Functions Algebraic Test for Even and Odd Functions: • A function

Example 10 – Even and Odd Functions Determine whether each function is even, odd,

Example 10 – Solution b. h(x) = x 2 + 1 b. This function

Pre-Calculus Honors 1. 4: Shifting, Reflecting, and Stretching Graphs Copyright © Cengage Learning. All

Library of Parent Functions: Commonly Used Functions Label important characteristics of each parent function.

Vertical Shift Change each function so it shifts up 2 units from the parent

Horizontal Shift Change each function so it shifts right 3 units from the parent

Example 1 – Shifts in the Graph of a Function Compare the graph of

Example 1 – Solution cont’d Compare the graph of each function with the graph

Example 5 – Nonrigid Transformations Compare the graph of each function with the graph

Example 5 – Solution cont’d b. Similarly, the graph of g (x) = |

Pre-Calculus Honors 1. 3: Step Functions and Piecewise-Defined Functions HW: p. 38 (56 -62

Example 8 – Sketching a Piecewise-Defined Function Sketch the graph of f (x) =

Do Now: Sketch the piecewise function. 23

Slides: 23

Download presentation

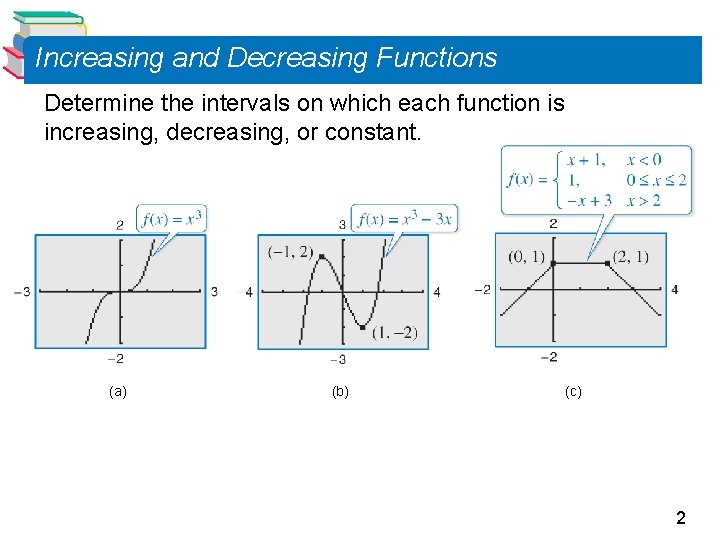
Increasing and Decreasing Functions Determine the intervals on which each function is increasing, decreasing, or constant. (a) (b) (c) 2

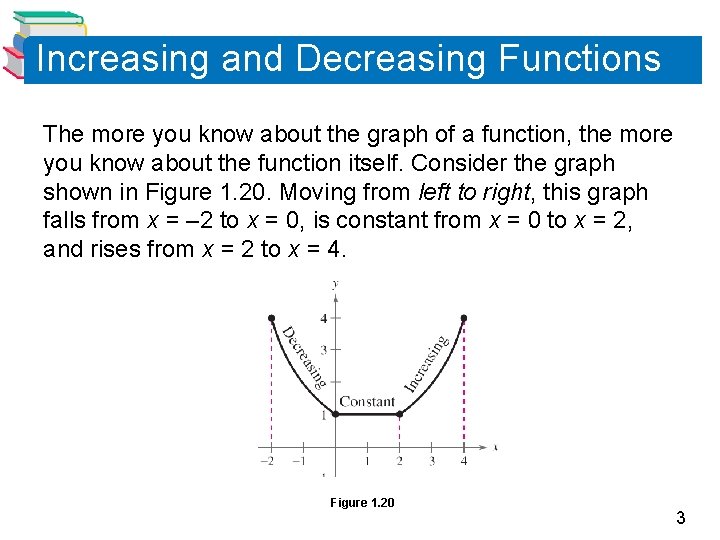
Increasing and Decreasing Functions The more you know about the graph of a function, the more you know about the function itself. Consider the graph shown in Figure 1. 20. Moving from left to right, this graph falls from x = – 2 to x = 0, is constant from x = 0 to x = 2, and rises from x = 2 to x = 4. Figure 1. 20 3

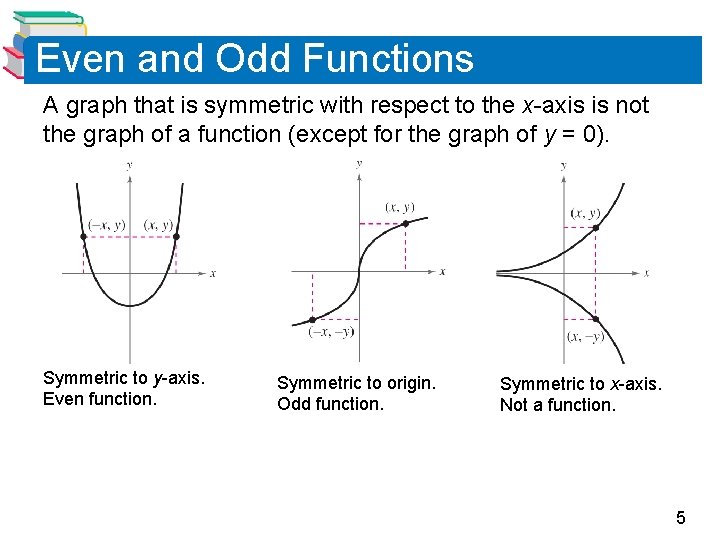
Even and Odd Functions • A function whose graph is symmetric with respect to the y -axis is an even function. • A function whose graph is symmetric with respect to the origin is an odd function. • A graph has symmetry with respect to the y-axis if whenever (x, y) is on the graph, then so is the point (–x, y). • A graph has symmetry with respect to the origin if whenever (x, y) is on the graph, then so is the point (–x, –y). • A graph has symmetry with respect to the x-axis if whenever (x, y) is on the graph, then so is the point (x, –y). 4

Even and Odd Functions A graph that is symmetric with respect to the x-axis is not the graph of a function (except for the graph of y = 0). Symmetric to y-axis. Even function. Symmetric to origin. Odd function. Symmetric to x-axis. Not a function. 5

Even and Odd Functions Algebraic Test for Even and Odd Functions: • A function f is even when, for each x in the domain of f, f(-x) = f(x). • A function f is odd when, for each x in the domain of f, f(-x) = -f(x). 6

Example 10 – Even and Odd Functions Determine whether each function is even, odd, or neither. a. g(x) = x 3 – x b. h(x) = x 2 + 1 c. f (x) = x 3 – 1 Solution: a. This function is odd because g (–x) = (–x)3+ (–x) = –x 3 + x = –(x 3 – x) = –g(x). 7

Example 10 – Solution b. h(x) = x 2 + 1 b. This function is even because h (–x) = (–x)2 + 1 = x 2 + 1 = h (x). c. f (x) = x 3 – 1 c. Substituting –x for x produces f (–x) = (–x)3 – 1 = –x 3 – 1. So, the function is neither even nor odd. 8

Library of Parent Functions: Commonly Used Functions Label important characteristics of each parent function. 10

Vertical Shift Change each function so it shifts up 2 units from the parent function. 11

Horizontal Shift Change each function so it shifts right 3 units from the parent function. 12

Vertical and Horizontal Shifts 13

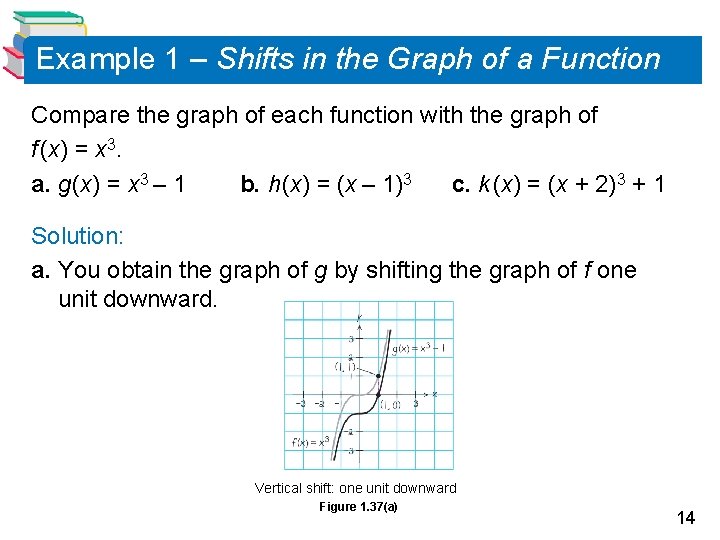
Example 1 – Shifts in the Graph of a Function Compare the graph of each function with the graph of f (x) = x 3. a. g (x) = x 3 – 1 b. h (x) = (x – 1)3 c. k (x) = (x + 2)3 + 1 Solution: a. You obtain the graph of g by shifting the graph of f one unit downward. Vertical shift: one unit downward Figure 1. 37(a) 14

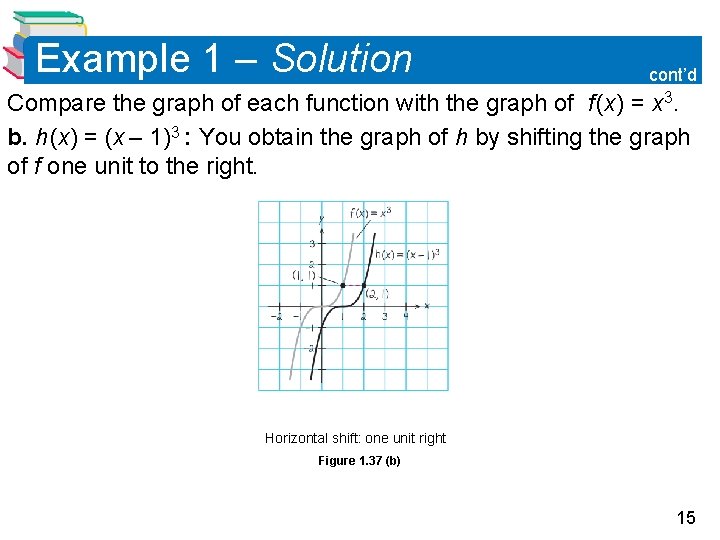
Example 1 – Solution cont’d Compare the graph of each function with the graph of f (x) = x 3. b. h (x) = (x – 1)3 : You obtain the graph of h by shifting the graph of f one unit to the right. Horizontal shift: one unit right Figure 1. 37 (b) 15

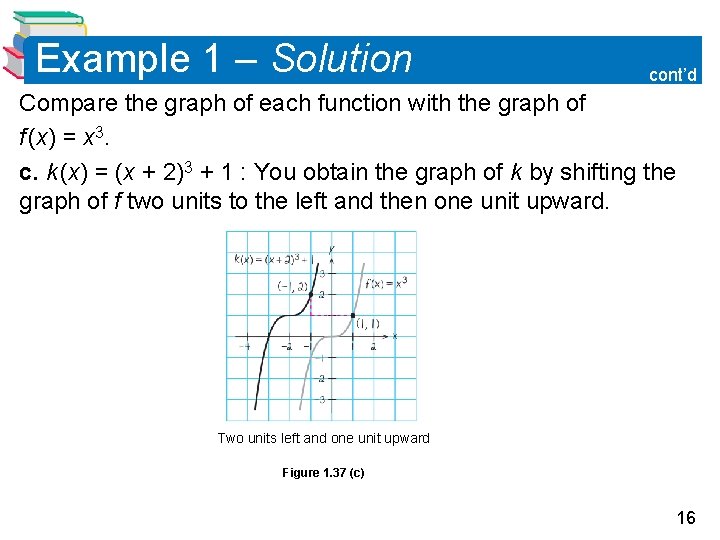
Example 1 – Solution cont’d Compare the graph of each function with the graph of f (x) = x 3. c. k (x) = (x + 2)3 + 1 : You obtain the graph of k by shifting the graph of f two units to the left and then one unit upward. Two units left and one unit upward Figure 1. 37 (c) 16

Reflecting Graphs 17

Example 5 – Nonrigid Transformations Compare the graph of each function with the graph of f (x) = | x |. a. h (x) = 3| x | b. g (x) = | x | Solution: a. Relative to the graph of f (x) = | x |, the graph of h (x) = 3| x | = 3 f (x) is a vertical stretch (each y-value is multiplied by 3) of the graph of f (See Figure 1. 45. ) Figure 1. 45 18

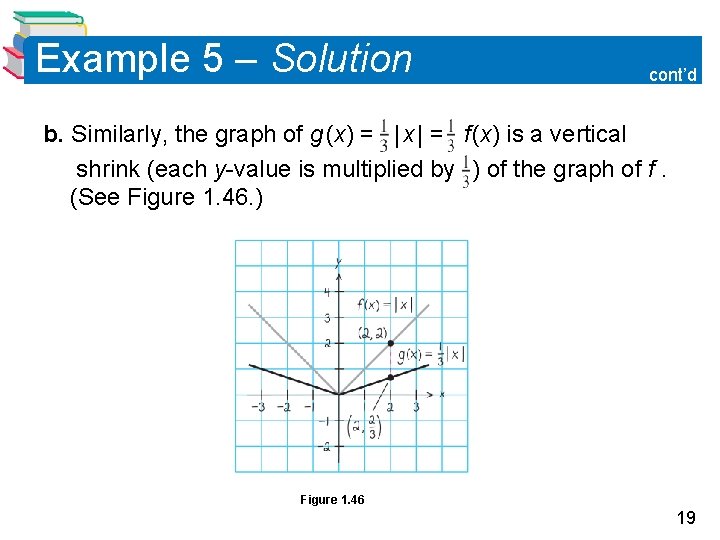
Example 5 – Solution cont’d b. Similarly, the graph of g (x) = | x | = f (x) is a vertical shrink (each y-value is multiplied by ) of the graph of f. (See Figure 1. 46. ) Figure 1. 46 19

Example 8 – Sketching a Piecewise-Defined Function Sketch the graph of f (x) = 2 x + 3, x ≤ 1 –x + 4, x > 1 by hand. 21

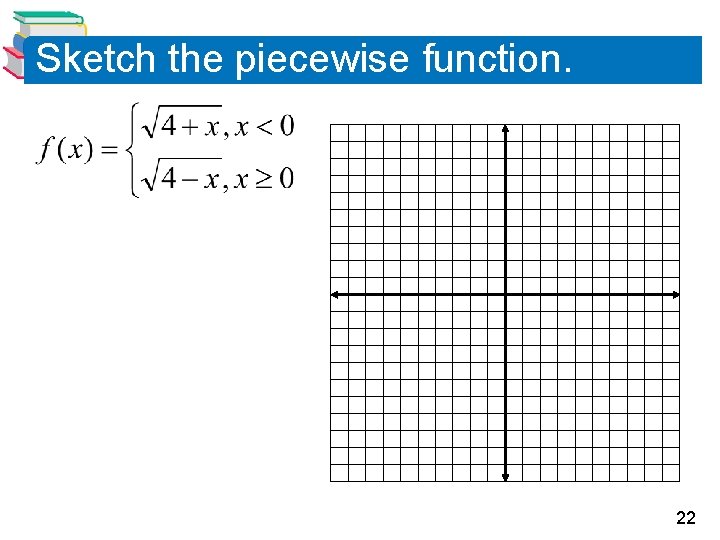
Sketch the piecewise function. 22

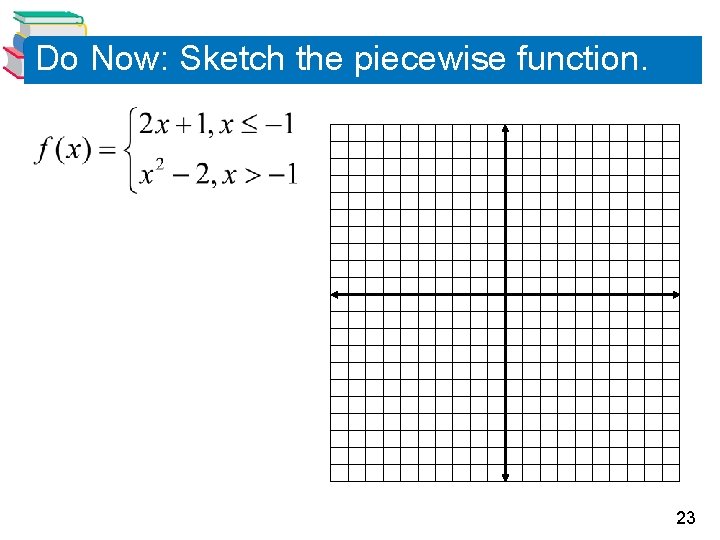
Do Now: Sketch the piecewise function. 23